浙教版数学七年级上册《角的和差》同步练习 4页

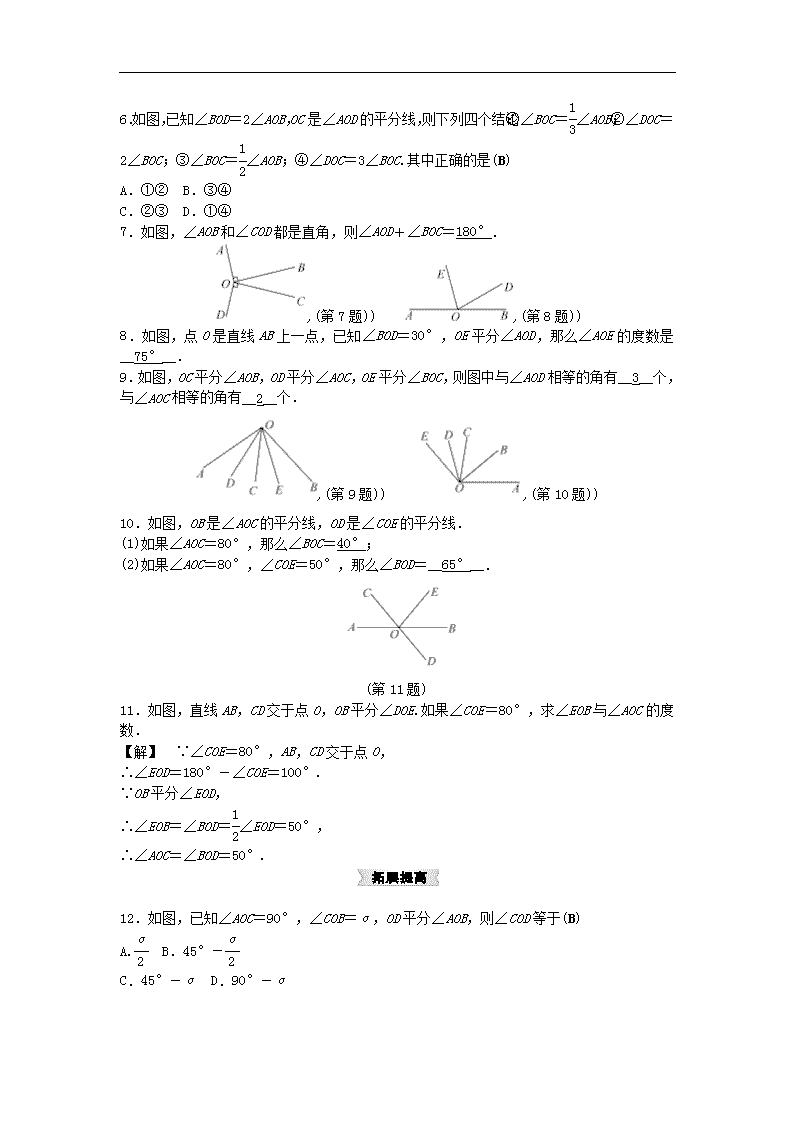
6．7 角的和差 1．点 P 在∠MAN 内，现有如下等式：①∠PAM＝1 2 ∠MAN；②∠PAN＝1 2 ∠MAN；③∠PAM＝∠PAN； ④∠MAN＝2∠PAN.其中能表示 AP 是角平分线的等式有(D) A．1 个 B．2 个 C．3 个 D．4 个 2．如图，一副三角尺(直角顶点重合)摆放在桌面上，若∠AOD＝150°，则∠BOC 等于(A) A．30° B．45° C．50° D．60° ,(第 2 题)) ,(第 3 题)) 3．如图，∠AOC＝∠BOD＝90°，下列结论中正确的个数是(C) ①∠AOB＝∠COD ②∠AOD＝3∠BOC ③∠AOD＋∠BOC＝∠AOC＋∠BOD A．0 B．1 C．2 D．3 4．如图，OD 是∠AOC 的平分线，OC 是∠BOD 的平分线，且∠COD＝40°，则∠AOB＝(C) A．80° B．100° C．120° D．160° (第 4 题) (第 5 题) 5．如图，将长方形 ABCD 沿 AE 折叠，使点 D 落在 BC 边上的点 F 处，若∠BAF＝60°，则∠DAE ＝(A) A．15° B．30° C．45° D．60° (第 6 题) 6．如图，已知∠BOD＝2∠AOB，OC 是∠AOD 的平分线，则下列四个结论：①∠BOC＝1 3 ∠AOB； ②∠DOC＝2∠BOC；③∠BOC＝1 2 ∠AOB；④∠DOC＝3∠BOC.其中正确的是(B) A．①② B．③④ C．②③ D．①④ 7．如图，∠AOB 和∠COD 都是直角，则∠AOD＋∠BOC＝180°． ,(第 7 题)) ,(第 8 题)) 8．如图，点 O 是直线 AB 上一点，已知∠BOD＝30°，OE 平分∠AOD，那么∠AOE 的度数是 __75°__． 9．如图，OC 平分∠AOB，OD 平分∠AOC，OE 平分∠BOC，则图中与∠AOD 相等的角有__3__ 个，与∠AOC 相等的角有__2__个． ,(第 9 题)) ,(第 10 题)) 10．如图，OB 是∠AOC 的平分线，OD 是∠COE 的平分线． (1)如果∠AOC＝80°，那么∠BOC＝40°； (2)如果∠AOC＝80°，∠COE＝50°，那么∠BOD＝__65°__． (第 11 题) 11．如图，直线 AB，CD 交于点 O，OB 平分∠DOE.如果∠COE＝80°，求∠EOB 与∠AOC 的度 数． 【解】 ∵∠COE＝80°，AB，CD 交于点 O， ∴∠EOD＝180°－∠COE＝100°. ∵OB 平分∠EOD， ∴∠EOB＝∠BOD＝1 2 ∠EOD＝50°， ∴∠AOC＝∠BOD＝50°. 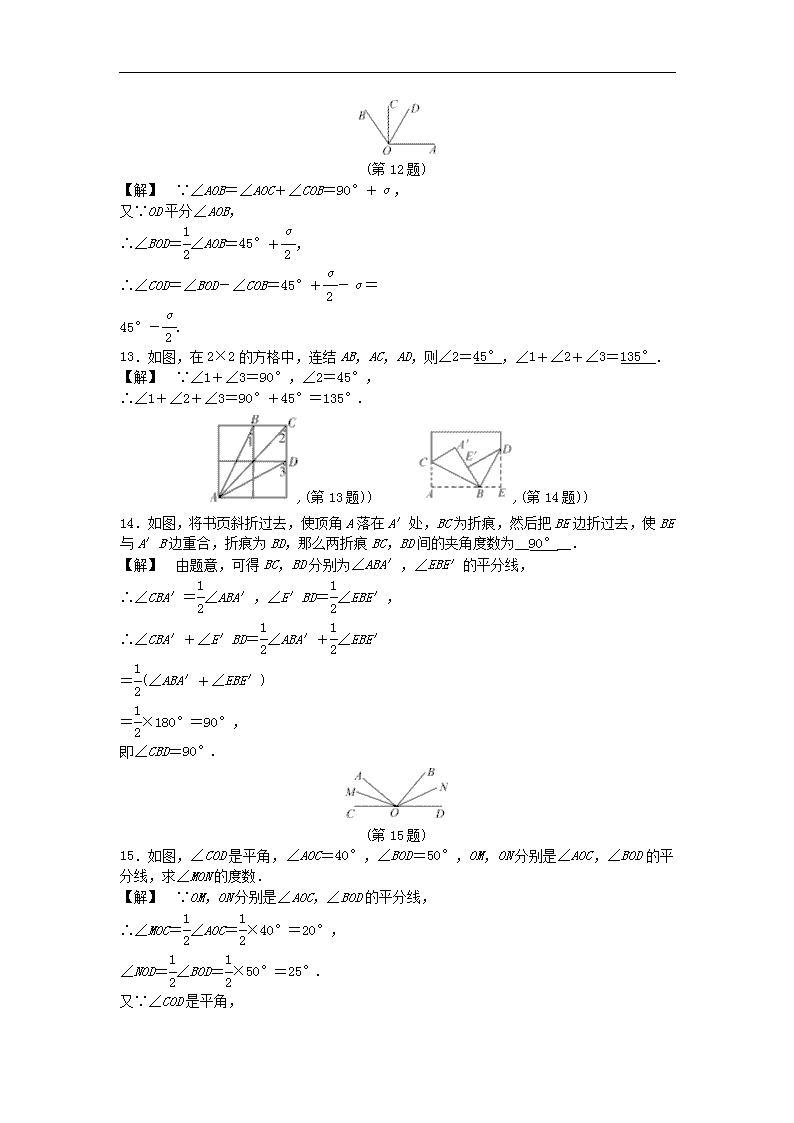12．如图，已知∠AOC＝90°，∠COB＝α，OD 平分∠AOB，则∠COD 等于(B) A.α 2 B．45°－α 2 C．45°－α D．90°－α (第 12 题) 【解】 ∵∠AOB＝∠AOC＋∠COB＝90°＋α， 又∵OD 平分∠AOB， ∴∠BOD＝1 2 ∠AOB＝45°＋α 2 ， ∴∠COD＝∠BOD－∠COB＝45°＋α 2 －α＝ 45°－α 2 . 13．如图，在 2×2 的方格中，连结 AB，AC，AD，则∠2＝45°，∠1＋∠2＋∠3＝135°． 【解】 ∵∠1＋∠3＝90°，∠2＝45°， ∴∠1＋∠2＋∠3＝90°＋45°＝135°. ,(第 13 题)) ,(第 14 题)) 14．如图，将书页斜折过去，使顶角 A 落在 A′处，BC 为折痕，然后把 BE 边折过去，使 BE 与 A′B 边重合，折痕为 BD，那么两折痕 BC，BD 间的夹角度数为__90°__． 【解】 由题意，可得 BC，BD 分别为∠ABA′，∠EBE′的平分线， ∴∠CBA′＝1 2 ∠ABA′，∠E′BD＝1 2 ∠EBE′， ∴∠CBA′＋∠E′BD＝1 2 ∠ABA′＋1 2 ∠EBE′ ＝1 2 (∠ABA′＋∠EBE′) ＝1 2 ×180°＝90°， 即∠CBD＝90°. (第 15 题) 15．如图，∠COD 是平角，∠AOC＝40°，∠BOD＝50°，OM，ON 分别是∠AOC，∠BOD 的平 分线，求∠MON 的度数． 【解】 ∵OM，ON 分别是∠AOC，∠BOD 的平分线， ∴∠MOC＝1 2 ∠AOC＝1 2 ×40°＝20°， ∠NOD＝1 2 ∠BOD＝1 2 ×50°＝25°. 又∵∠COD 是平角， ∴∠MOC＋∠MON＋∠NOD＝180°， ∴20°＋∠MON＋25°＝180°， ∴∠MON＝135°. 16．如图，已知∠AOB 是直角，∠BOC＝30°，OM 平分∠AOC，ON 平分∠BOC. (1)求∠MON 的度数； (2)若∠AOB＝α，其他条件不变，求∠MON 的度数． (第 16 题) 【解】 (1)∵∠AOB＝90°，∠BOC＝30°， ∴∠AOC＝∠AOB＋∠BOC＝120°. ∵OM 平分∠AOC，ON 平分∠BOC， ∴∠MOC＝1 2 ∠AOC＝1 2 ×120°＝60°， ∠NOC＝1 2 ∠BOC＝1 2 ×30°＝15°. ∴ ∠MON＝∠ MOC－∠NOC＝ 60°－15°＝45°. (2)∵∠AOB＝α ，∠BOC＝30°， ∴∠AOC＝∠AOB＋∠BOC＝α＋30°. ∵OM 平分∠AOC，ON 平分∠BOC， ∴∠MOC＝1 2 ∠AOC＝α＋30° 2 ， ∠NOC＝1 2 ∠BOC＝15°. ∴∠MON＝∠ MOC－∠NOC＝α＋30° 2 －15°＝α 2 .