北师大版七年级上册数学期中测试题附答案 6页

北师大版七年级上册数学期中测试题附答案 ‎(时间：120分钟　　　满分：120分)‎ 6‎ 一、选择题(本大题共6小题，每小题3分，共18分．每小题只有一个正确选项)‎ ‎1．－2 020的相反数是(　A　)‎ A．2 020 B．－2 020 ‎ C. D．－ ‎2．如图①，将正方形沿面AB′C截下，则截下的几何体如图②是(　A　)‎ A．三棱锥 B．三棱柱 C．四棱锥 D．四棱柱 ‎3．拒绝“餐桌浪费”，刻不容缓．据统计全国每年浪费食物总量约500亿千克，这个数据用科学记数法表示为(　D　)‎ A．0.5×1011 千克 B．50×109 千克 C．5×109 千克 D．5×1010 千克 ‎4．(吉安期末)若x2＋3x－5的值为7，则3x2＋9x－2的值为(　C　)‎ A．0 B．24 C．34 D．44‎ ‎5．实数a，b在数轴上的位置如图，则|a＋b|－|a－b|等于(　A　)‎ A．2a B．2b C．2b－2a D．2b＋2a ‎6．观察下列图形及图形所对的算式，根据你发现的规律计算1＋8＋16＋24＋…＋8n(n为正整数)的结果是(　D　)‎ A．n2 B．(2n－1)2 ‎ C．(n＋2)2 D．(2n＋1)2‎ 二、填空题(本大题共6小题，每小题3分，共18分)‎ ‎7．平方和绝对值都是它本身的相反数的数是 0，－1 ．‎ ‎8．如图，有一个窗户，上部是半圆，下部是正方形，正方形的边长为4a cm，此窗户的面积是 2(8＋π)a2 cm2.‎ ‎ ‎ 6‎ 第8题图　 　 第12题图 ‎9．下列图形经过折叠不能围成棱柱的是 ② ．‎ ‎ ‎ ‎　①　　　　　②　　　　　　③　　　　④‎ ‎10．多项式x2－2kxy－3y2＋6xy－8化简后不含xy项，则k＝ 3 ．‎ ‎11．已知|x－y|＝y－x，且|x|＝3，|y|＝4，则(x＋y)3的值为 343或1 ．‎ ‎12．如图，对于大于或等于2的自然数n的平方进行如下“分裂”，分裂成n个连续奇数的和，则自然数92的分裂数中最大的数是 17 ．‎ 选择、填空题答题卡 一、选择题(每小题3分，共18分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 得分 答案 A A D C A D 二、填空题(每小题3分，共18分) 得分：______‎ ‎7． 0，－1 　8. 2(8＋π)a2 　9. ② ‎ ‎10． 3　 11. 343或1　 12. 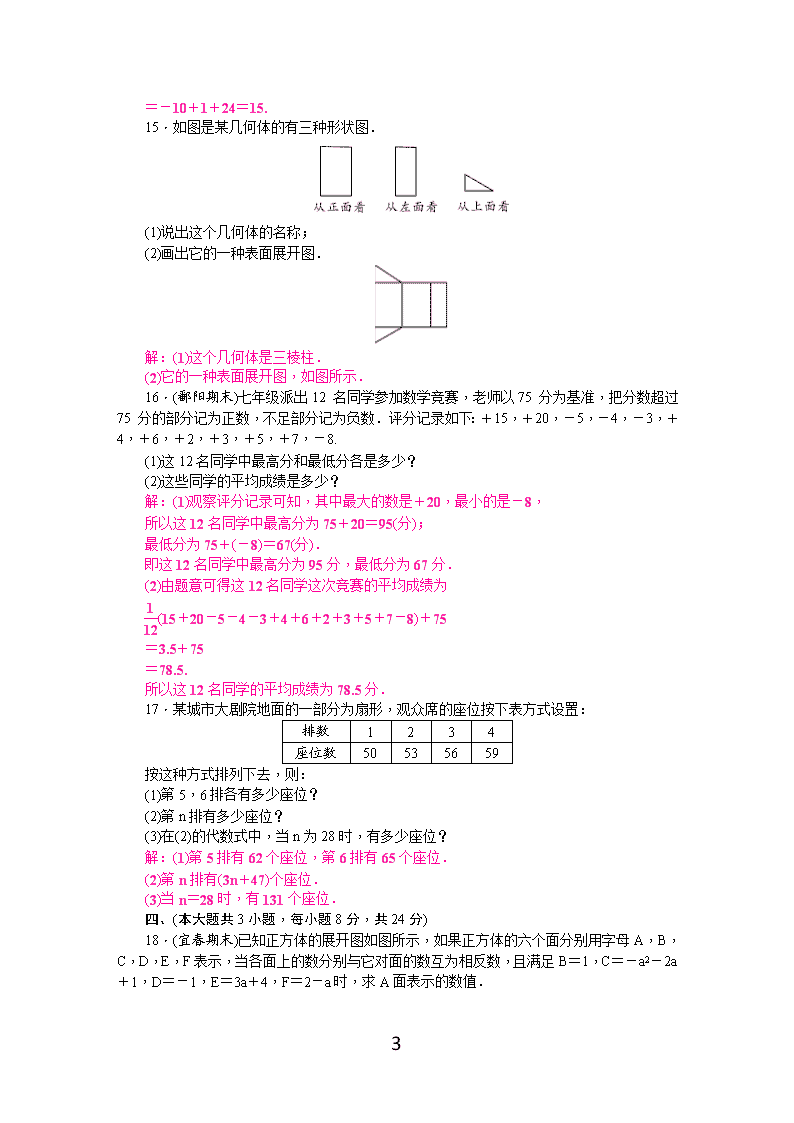17 ‎ 三、(本大题共5小题，每小题6分，共30分)‎ ‎13．计算：‎ ‎(1)－3.25－＋(－6.75)＋；‎ 解：原式＝－3.25＋＋(－6.75)＋ ‎＝[(－3.25)＋(－6.75)]＋ ‎＝(－10)＋2‎ ‎＝－8.‎ ‎(2)100＋16÷(－2)4－－|－100|.‎ 解：原式＝100＋16÷16－－100‎ ‎＝1－ ‎＝.‎ ‎14．(九江期末)先化简，再求值：－3(2x2－xy)－4(－6＋xy＋x2)，其中x＝1，y＝－1.‎ 解：原式＝－6x2＋3xy＋24－4xy－4x2‎ ‎＝－10x2－xy＋24.‎ 当x＝1，y＝－1时，‎ 原式＝－10×12－1×(－1)＋24‎ 6‎ ‎＝－10＋1＋24＝15.‎ ‎15．如图是某几何体的有三种形状图．‎ ‎(1)说出这个几何体的名称；‎ ‎(2)画出它的一种表面展开图．‎ 解：(1)这个几何体是三棱柱．‎ ‎(2)它的一种表面展开图，如图所示．‎ ‎16．(鄱阳期末)七年级派出12 名同学参加数学竞赛，老师以75 分为基准，把分数超过75 分的部分记为正数，不足部分记为负数．评分记录如下：＋15，＋20，－5，－4，－3，＋4，＋6，＋2，＋3，＋5，＋7，－8.‎ ‎(1)这12名同学中最高分和最低分各是多少？‎ ‎(2)这些同学的平均成绩是多少？‎ 解：(1)观察评分记录可知，其中最大的数是＋20，最小的是－8，‎ 所以这12名同学中最高分为75＋20＝95(分)；‎ 最低分为75＋(－8)＝67(分)．‎ 即这12名同学中最高分为95分，最低分为67分．‎ ‎(2)由题意可得这12名同学这次竞赛的平均成绩为 (15＋20－5－4－3＋4＋6＋2＋3＋5＋7－8)＋75‎ ‎＝3.5＋75‎ ‎＝78.5.‎ 所以这12名同学的平均成绩为78.5分．‎ ‎17．某城市大剧院地面的一部分为扇形，观众席的座位按下表方式设置：‎ 排数 ‎1‎ ‎2‎ ‎3‎ ‎4‎ 座位数 ‎50‎ ‎53‎ ‎56‎ ‎59‎ 按这种方式排列下去，则：‎ ‎(1)第5，6排各有多少座位？‎ ‎(2)第n排有多少座位？‎ ‎(3)在(2)的代数式中，当n为28时，有多少座位？‎ 解：(1)第5排有62个座位，第6排有65个座位．‎ ‎(2)第n排有(3n＋47)个座位．‎ ‎(3)当n＝28时，有131个座位．‎ 四、(本大题共3小题，每小题8分，共24分)‎ ‎18．(宜春期末)已知正方体的展开图如图所示，如果正方体的六个面分别用字母A，B，C，D，E，F表示，当各面上的数分别与它对面的数互为相反数，且满足B＝1，C＝－a2－2a＋1，D＝－1，E＝3a＋4，F＝2－a时，求A面表示的数值．‎ 6‎ 解：因为E面和F面的数互为相反数，‎ 所以3a＋4＋2－a＝0，‎ 所以a＝－3，‎ 把a＝－3代入C＝－a2－2a＋1，解得C＝－2，‎ 因为A面与C面表示的数互为相反数，‎ 所以A面表示的数值是2.‎ ‎19．已知a，b均为有理数，现我们定义一种新的运算，规定：a#b＝a2＋ab－5，例如：1#2＝12＋1×2－5＝－2.求：‎ ‎(1)(－3)#6的值；‎ ‎(2)－[(－5)#9]的值．‎ 解：(1)(－3)#6＝(－3)2＋(－3)×6－5‎ ‎＝9－18－5‎ ‎＝－14.‎ ‎(2)－[(－5)#9]‎ ‎＝－[(－5)2＋(－5)×9－5]‎ ‎＝(4－3－5)－(25－45－5)‎ ‎＝－4＋25‎ ‎＝21.‎ ‎20．若代数式(4x2－mx－3y＋4)－(8nx2－x＋2y－3)的值与字母x的取值无关，求代数式(－m2＋2mn－n2)－2(mn－3m2)＋3(2n2－mn)的值．‎ 解：(4x2－mx－3y＋4)－(8nx2－x＋2y－3)‎ ‎ ＝4x2－mx－3y＋4－8nx2＋x－2y＋3‎ ‎ ＝(4－8n)x2＋(1－m)x－5y＋7.‎ 因为上式的值与字母x的取值无关，‎ 所以4－8n＝0，1－m＝0，即m＝1，n＝.‎ ‎(－m2＋2mn－n2)－2(mn－3m2)＋3(2n2－mn)＝－m2＋2mn－n2－2mn＋6m2＋6n2－3mn ‎＝5m2＋5n2－3mn ‎＝5×12＋5×－3×1×＝.‎ 五、(本大题共2小题，每小题9分，共18分)‎ ‎21．吉州区某文具店出售A，B两种文具．A文具每套200元，B文具每套40元，该店开展促销活动，向客户提供两种优惠方案：①买一套A文具送一套B文具．②A文具和B文具都按定价的90%付款．现某客户要到该店购买A文具20套，B文具x套(x＞20)‎ ‎(1)若该客户按方案①购买需付款____元(用含x的代数式表示)；‎ 6‎ 若该客户按方案②购买需付款____元(用含x的代数式表示)；‎ ‎(2)当x＝30时，通过计算说明按哪种方案购买较为合算．‎ 解：(1)该客户按方案①购买需付款：‎ ‎3 200＋40x；‎ 该客户按方案②购买需付款：3 600＋36x；‎ 故答案为(3 200＋40x)；(3 600＋36x)．‎ ‎(2)当x＝30时，按方案①购买需付款：‎ ‎3 200＋40×30＝4 400(元)；‎ 按方案②购买需付款：‎ ‎3 600＋36×30＝4 680(元)．‎ 答：当x＝30时，选择方案①购买较为合算．‎ ‎22．将连续的奇数1，3，5，7，9…排成如图的数阵．‎ ‎(1)十字框中的五个数的和与中间数15有什么关系？‎ ‎(2)设中间数为a，用式子表示十字框中五个数之和；‎ ‎(3)十字框中五个数之和能等于2 020吗？若能，请写出这五个数；若不能，请说明理由．‎ 解：(1)5＋13＋15＋17＋25＝15×5，‎ 故十字框中的五个数的和等于中间的数15的5倍．‎ ‎(2)设中间的数为a，则十字框中的五个数字之和为a－10＋a－2＋a＋a＋2＋a＋10＝5a，‎ 故五个数字之和为5a.‎ ‎(3)不能．理由：‎ ‎5a＝2 020，‎ 解得a＝404，‎ 而a的个位不能为4，‎ 故十字框中五个数字之和不能等于2 020.‎ 六、(本大题共12分)‎ ‎23．(上饶期末)在数轴上有A，B，C，D四个点，这四个点表示的数分别为－3，－1，2，4，如下图．‎ ‎(1)计算|－3－(－1)|，|4－2|，|4－(－3)|；再观察数轴，写出A，B两点的距离，C，D两点的距离，和A，D两点的距离；‎ ‎(2)A，B的距离______|－3－(－1)|，C，D两点的距离______|4－2|，A，D两点的距离______|4－(－3)|；(选填“＞”“＝”或“＜”)‎ ‎(3)如果点P，Q两点表示的数分别为x，y，那么P，Q两点的距离＝______；‎ ‎(4)若|x－(－3)|＋|x－4|＝7，数x代表的点R在数轴上什么位置？x介于哪两个数之间？‎ 解：(1)|－3－(－1)|＝2，‎ ‎|4－2|＝2，‎ ‎|4－(－3)|＝7.‎ 6‎ A，B两点的距离为2，C，D两点的距离为2，‎ A，D两点的距离为7.‎ ‎(2)观察数轴，可得 A，B的距离＝|－3－(－1)|，‎ C，D两点的距离＝|4－2|，‎ A，D两点的距离＝|4－(－3)|.‎ 故答案为＝　＝　＝.‎ ‎(3)P，Q两点的距离＝|x－y|.‎ ‎(4)根据|x－(－3)|＋|x－4|＝7可知点R在点A，D之间的线段上，此时x在－3与4之间即－3≤x≤4.‎ 6‎ 6‎