七年级下册数学教案6-1 第3课时 平方根 人教版 4页

第六章 实数 ‎6.1 平方根 教学备注 ‎【自学指导提示】‎ 学生在课前完成自主学习部分 第2课时 用计算器求算术平方根及大小比较 学习目标：1.了解平方根的概念，会求某些非负数的平方根，明确算术平方根与平方根的区别与联系.‎ ‎2.独立思考，合作交流，经历从平方运算到求平方根的演变过程，感受二者的互逆关系..‎ ‎3.激情投入，善于发现问题和提出问题，感受学习数学的乐趣.‎ 重点：平方根的概念及平方根的求法.‎ 难点：求非负数的平方根.‎ 自主学习 一、知识链接 ‎1.什么叫做算术平方根？‎ ‎2.计算：（1）22= ，（-2）2= .‎ ‎（2）= ，= .‎ 二、新知预习 ‎1.一般的，如果一个数的平方等于a，那么这个数叫做a的 或 .正数a的平方根可以用符号“ ”表示，读作 .‎ ‎2.正数的平方根有 个，它们互为 ；0的平方根是 ，负数 平方根.‎ ‎3.求一个数a的平方根的运算，叫做 .‎ 三、自学自测 ‎1.若x2=7，则称x为 的平方根，记作x= ；其中是7的 ‎ 平方根，7的负的平方根是 .‎ ‎2.下列说法中，正确的有 个.‎ ‎（1）4是16的一个平方根；（2）16的平方根是4；（3）-36的平方根是±6；（4）-a2一定没有平方根.‎ 四、我的疑惑 ‎___________________________________________________________________________________________________________‎ ‎___________________________________________‎ 教学备注 配套PPT讲授 ‎1.情景引入 ‎（见幻灯片3）‎ ‎2.探究点新知讲授 ‎（见幻灯片5-21）‎ 课堂探究 一、 要点探究 探究点1：平方根的定义及性质 填一填:‎ ‎（1）4的平方等于16，那么16的算术平方根就是________；‎ ‎（2）的平方等于，那么的算术平方根就是_______；‎ ‎（3）展厅地面为正方形，其面积是49 m2，则其边长为______m..‎ ‎（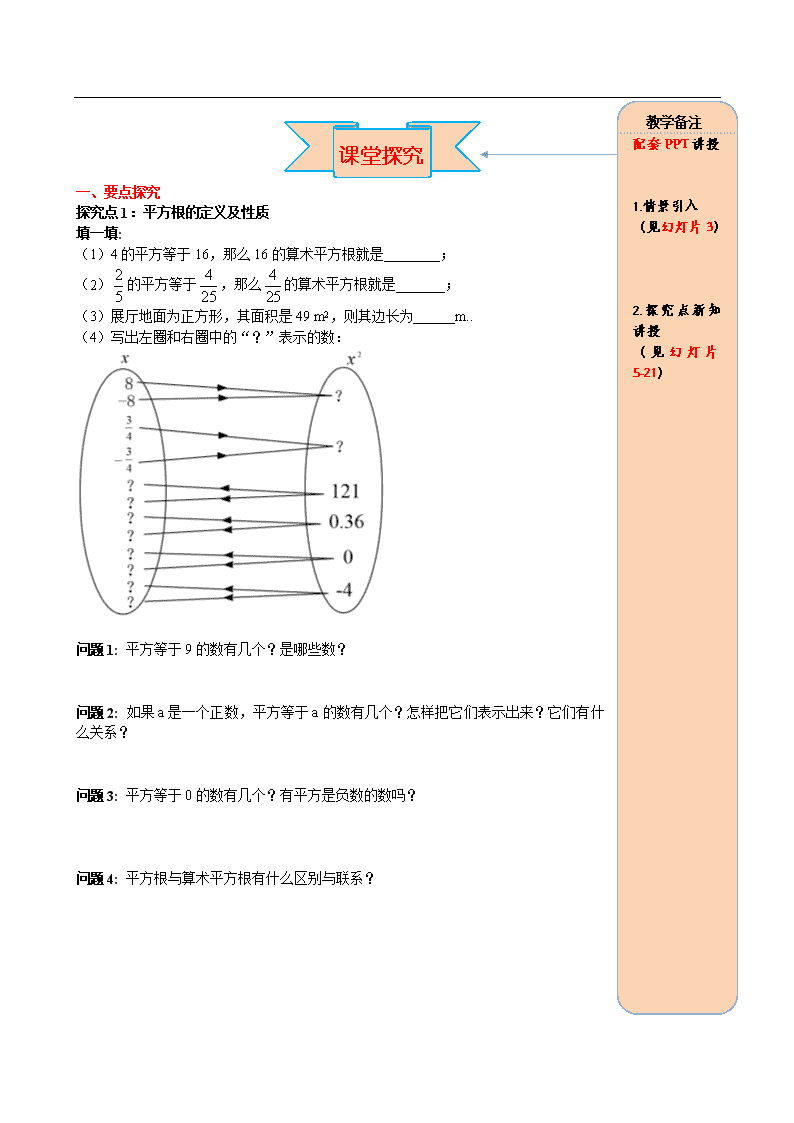4）写出左圈和右圈中的“？”表示的数： ‎ ‎[来源:Zxxk.Com]‎ 问题1: 平方等于9的数有几个？是哪些数？‎ 问题2: 如果a是一个正数，平方等于a的数有几个？怎样把它们表示出来？它们有什么关系？[来源:学科网ZXXK]‎ 问题3: 平方等于0的数有几个？有平方是负数的数吗？‎ 问题4: 平方根与算术平方根有什么区别与联系？‎ 要点归纳：‎ ‎1.平方根的性质：‎ ‎（1）正数有两个平方根，两个平方根互为相反数.‎ ‎（2）0的平方根还是0.‎ ‎（3）负数没有平方根.‎ ‎2.平方根与算术平方根的联系与区别： ‎ 联系：‎ ‎（1）包含关系：平方根包含算术平方根，算术平方根是平方根的一种.‎ ‎（2）只有非负数才有平方根和算术平方根.‎ ‎（3）0的平方根是0，算术平方根也是0.‎ 区别：‎ ‎（1）个数不同：一个正数有两个平方根，但只有一个算术平方根. ‎ ‎（2）表示法不同：平方根表示为，而算术平方根表示为.‎ 典例精析 例1.一个正数的两个平方根分别是2a＋1和a－4，求这个数．‎ ‎ ‎ 方法总结:一个正数有两个平方根，它们互为相反数．‎ 例2.分别求下列各数的平方根：‎ ‎36，，1.21.[来源:学。科。网]‎ 例3.求下列各式的值：‎ ‎[来源:学.科.网]‎ 教学备注 配套PPT讲授 ‎2.探究点新知讲授 ‎（见幻灯片5-21）‎ 二、课堂小结[来源:学_科_网]‎ 平方根 平方根的概念 平方根的性质 开平方及相关运算 教学备注 配套PPT讲授 ‎3.课堂小结 ‎4.当堂检测 ‎（见幻灯片22-25）‎ 当堂检测 ‎1.下列说法正确的是_________‎ ‎① -3是9的平方根; ②25的平方根是5; ③ -36的平方根是-6; ‎ ‎④平方根等于0的数是0; ⑤64的算术平方根是8.‎ ‎2.下列说法不正确的是______‎ A.0的平方根是0 B.的平方根是2‎ C.非负数的平方根互为相反数 D.一个正数的算术平方根一定大于这个数的相反数 ‎3.判断下列说法是否正确.‎ ‎（1）是的一个平方根；‎ ‎（2）是6的算术平方根；‎ ‎（3）的值是±4； ‎ ‎（4）(-4)2的平方根是-4.‎ ‎4. 分别求 64，，6.25的平方根.‎ ‎5.求下列各式的值：‎ ‎（1）；（2）；（3）‎