人教版数学八下第十九章《一次函数》 4页

2015—2016学年度第二学期新课程素质能力测试八1.圆的面积公式S=πr2中的变量是A.S,B.S,,rC.S,rD.r22.变量x,y有如下关系：①x+y=10②y=③y=|x-3④y2=8x.其中y是x的函数的是A.①②②③④B.①②③C.①②D.①3.下列曲线中，不表示y是x的函数的是4.下列各点中，在直线y=-4x+1上的点是A.（-4，-17）B.（-6）C.（-1）D.（1，-5）5.已知正比例函数y=(k+5)x,且y随x的增大而减小，则k的取值范围是A.k＞5B.k＜5C.k＞-5D.k＜-56.在平面直角坐标系xoy中，点M(a,1)在一次函数y=-x+3的图象上，则点N(2a-1,a)所在的象限是A.一象限B.二象限C.四象限D.不能确定7.下列说法不正确的是A.正比例函数是一次函数的特殊形式B.一次函数不一定是正比例函数C.y=kx+b是一次函数D.2x-y=0是正比例函数8.经过一、二、四象限的函数是A.y=7B.y=-2xC.y=7-2xD.y=-2x-79.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小，则函数y=kx-k的图象大致是10.若方程x-2=0的解也是直线y=(2k-1)x+10与x轴的交点的横坐标，则k的值为A.2B.0C.-2D.±211.直线y=kx+b交坐标轴于A(-8,0),B(0,13)两点，则不等式kx+b≥0的解集为A.x≥-8B.x≤-8C.x≥13D.x≤1312.已知直线y1=2x与直线y2=-2x+4相交于点A.有以下结论：①点A的坐标为A(1,2);②当x=1时，两个函数值相等；③当x＜1时，y1＜y2④直线y1=2x与直线y2=2x-4在平面直角坐标系中的位置关系是平行.其中正确的是 A.①③④B.②③C.①②③④D.①②③二、填空题（本大题共4个小题，每小题3分，共12分。请把答案填在题中的横线上）。13.描述函数的方法有：①;②;③14.描点法画函数图象的一般步骤是：①;②;③15.若函数y=(n-3)x+n2-9是正比例函数，则n的值为16.四边形有2条对角线，五边形有5条对角线，六边形有9条对角线，……n边形有条对角线.三、解答题（本大题共8个小题，共72分。解答应写出文字说明、证明过程或演算步骤）。17．（满分8分）计算:（1）已知函数y=(x+1)(x-1)-1中自变量x=2,求函数值；（2）求直线L1:y=3x-2与L2:y=-3x+1的交点坐标.18．（满分8分）希望中学学生从2014年12月份开始每周喝营养牛奶，单价为2元/盒，总价y元随营养牛奶盒数x变化.指出其中的常量与变量，自变量与函数，并写出表示函数与自变量关系的式子.19.（满分8分）根据下列条件分别确定函数y=kx+b的解析式：（1）y与x成正比例，当x=2时，y=3;（2）直线y=kx+b经过点（2,4）与点（.20．（满分8分）如图正比例函数y=2x的图像与一次函数y=kx+b的图像交于点A（m,2）,一次函数的图像经过点B（-2，-1）与y轴交点为C与x轴交点为D.（1）求一次函数的解析式；（2）求C点的坐标；（3）求△AOD的面积。21．（满分8分）已知长方形周长为20.（1）写出长y关于宽x的函数解析式（x为自变量）；（2）在直角坐标系中，画出函数图像. 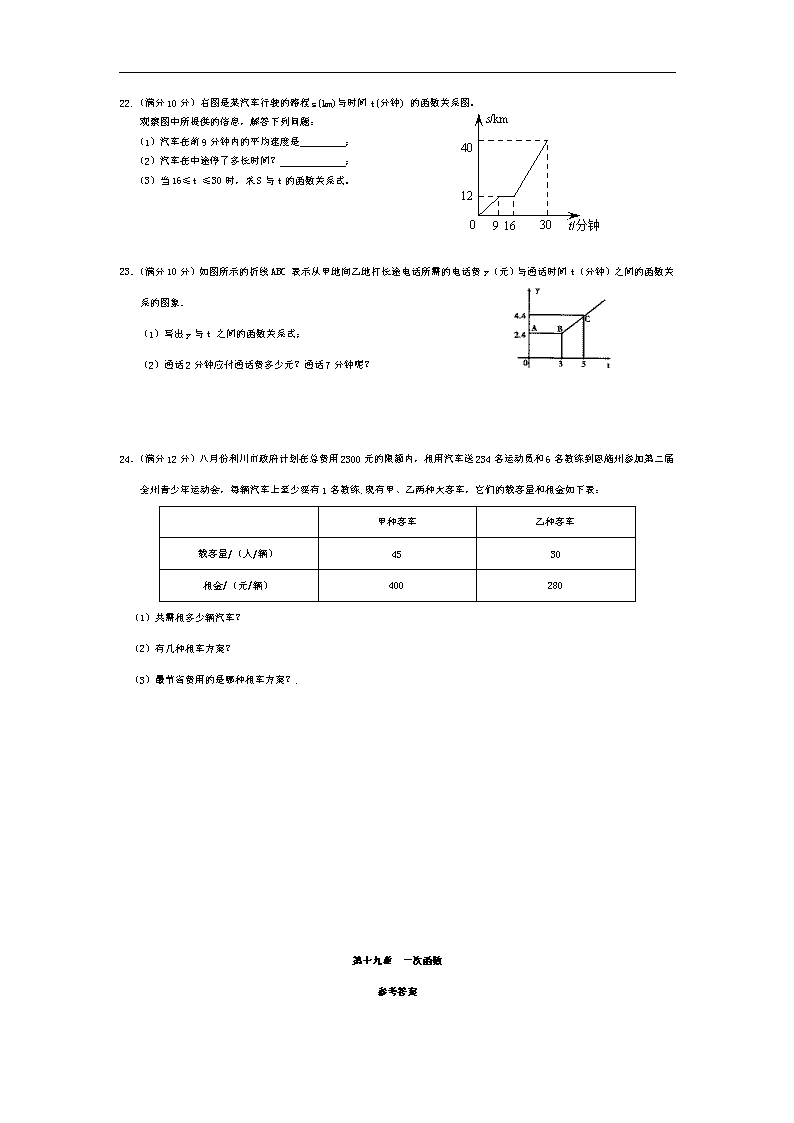091630t/分钟s/km401222.（满分10分）右图是某汽车行驶的路程s(km)与时间t(分钟)的函数关系图。观察图中所提供的信息，解答下列问题：（1）汽车在前9分钟内的平均速度是；（2）汽车在中途停了多长时间？；（3）当16≤t≤30时，求S与t的函数关系式。23．（满分10分）如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y（元）与通话时间t（分钟）之间的函数关系的图象．（1）写出y与t之间的函数关系式；（2）通话2分钟应付通话费多少元？通话7分钟呢？24．（满分12分）八月份利川市政府计划在总费用2300元的限额内，租用汽车送234名运动员和6名教练到恩施州参加第二届全州青少年运动会，每辆汽车上至少要有1名教练.现有甲、乙两种大客车，它们的载客量和租金如下表：　甲种客车乙种客车载客量/（人/辆）4530租金/（元/辆）400280（1）共需租多少辆汽车？（2）有几种租车方案？（3）最节省费用的是哪种租车方案？.第十九章 一次函数参考答案 一、1-12CBBCDACCDCAC二、13、列表、图像、解析式14、列表、描点、连线15、-316、n(n-3)/2三、17、（1）y=6；（2）（1/2，-1/2）18、y=2x;常量：2；变量：x,y；自变量：x；y是x的函数19、（1）y=3x/2;(2)y=13x/5-6/520、（1）y=x+1;(2)C(0,1);（3）121、（1）y=10-x(0＜x＜10)；（2）略22、（1）80km/h；（2）7分钟；（3）S=2t-2023、（1）当03时，y=t-0.6；（2）2.4元；6.4元24、（1）由每辆汽车上至少要有1名老师，汽车总数不能大于6辆；又要保证240名师生有车坐且汽车总数不能小于240/45（取整为6）辆，综合起来可知汽车总数为6辆．（2）设租用m辆甲种客车，则租车费用Q（单位：元）是m的函数，即Q=400m+280（6-m）；化简为：Q=120m+1680，依题意有：120m+1680≤2300，∴m≤31/6，即m≤5又要保证240名师生有车坐，m不小于4,所以有两种租车方案:方案一：4辆甲种客车，2辆乙种客车；方案二：5辆甲种客车，1辆乙种客车．（3）由（2）知Q=120m+1680∵Q随m增加而增加，∴当m=4时，Q最少为2160元．即方案一最节省费用。