八年级下数学课件八年级下册数学课件《平行四边形的判定》 北师大版 (7)_北师大版 (2) 8页

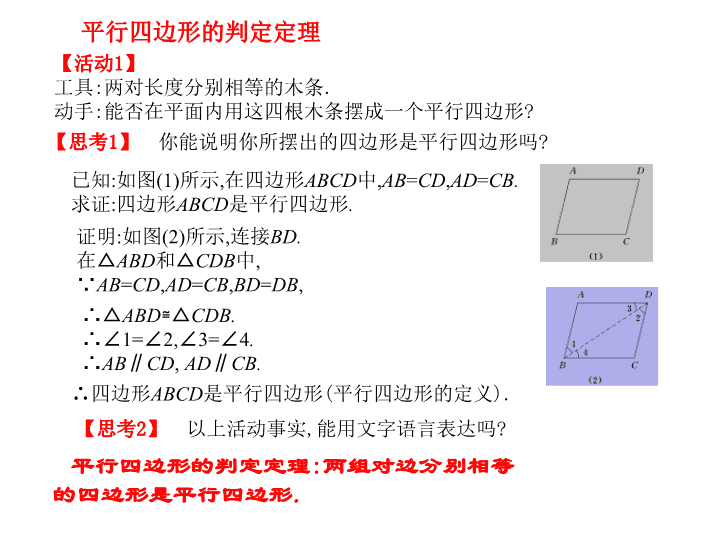
八年级数学·下新课标[北师]第六章平行四边形平行四边形的判定（第1课时） 学习新知问题思考平行四边形具有什么性质?①平行四边形是中心对称图形,两条对角线的交点是它的对称中心.②边:平行四边形的对边相等.③角:平行四边形的对角相等.④对角线:平行四边形的对角线互相平分.现在同学们拿出每人准备好的两根等长的小木条,两个同学合作,把一个人的相等的两根小木条作为一个四边形的一组对边,另一个同学的作为四边形的另一组对边,组成一个四边形,能行吗? 平行四边形的判定定理【活动1】工具:两对长度分别相等的木条.动手:能否在平面内用这四根木条摆成一个平行四边形?【思考1】你能说明你所摆出的四边形是平行四边形吗?已知:如图(1)所示,在四边形ABCD中,AB=CD,AD=CB.求证:四边形ABCD是平行四边形.证明:如图(2)所示,连接BD.在△ABD和△CDB中,∵AB=CD,AD=CB,BD=DB,∴△ABD≌△CDB.∴∠1=∠2,∠3=∠4.∴AB∥CD,AD∥CB.∴四边形ABCD是平行四边形(平行四边形的定义).【思考2】以上活动事实,能用文字语言表达吗?平行四边形的判定定理:两组对边分别相等的四边形是平行四边形. 【活动2】工具:两根长度相等的木条,两条平行线.动手:利用两根长度相等的木条能摆出以木条顶端为顶点的平行四边形吗?【思考1】你能说明你所摆出的四边形是平行四边形吗?已知:如图(1)所示,在四边形ABCD中,ABCD.求证:四边形ABCD是平行四边形.证明:如图(2)所示,连接AC.∵AB∥CD,∴∠BAC=∠DCA.又∵AB=CD,AC=CA,∴△ABC≌△CDA.∴BC=DA.∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).【思考2】以上活动事实,能用文字语言表达吗?平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形. (教材例1)已知:如图所示,在□ABCD中,E,F分别为AD和CB的中点.求证:四边形BFDE是平行四边形.〔解析〕本例是对平行四边形性质和判定的综合应用.要证明一个四边形是平行四边形,除了依据平行四边形的定义外,还可以考虑本课时刚学完的两个平行四边形的判定定理.证明:∵四边形ABCD是平行四边形,∴AD=CB(平行四边形的对边相等),AD∥CB(平行四边形的定义).∵E,F分别是AD和CB的中点,∴ED=AD,FB=CB.∴ED=FB,ED∥FB.∴四边形BFDE是平行四边形(一组对边平行且相等的四边形是平行四边形). 检测反馈1.(2015·新疆中考)四边形ABCD中,对角线AC与BD交于点O,下列条件中不能判定这个四边形是平行四边形的是()A.OA=OC,OB=ODB.AD∥BC,AB∥CDC.AB=CD,AD=BCD.AB∥DC,AD=BCD2.如图所示,在四边形ABCD中,AB∥CD,要使得四边形ABCD是平行四边形,应添加的条件是.(只填写一个条件,不使用图形以外的字母和线段)AB=CD(答案不唯一) 3.如图所示,在□ABCD中,点E,F分别在边AD,BC上,且BE∥DF,若∠EBF=45°,则∠EDF的度数是度.解析:由四边形ABCD是平行四边形,可得AD∥BC,又由BE∥DF,即可证得四边形BFDE是平行四边形,根据平行四边形的对角相等,即可求得∠EDF=∠EBF=45°.故填45.45 4.如图所示,四边形ABCD是平行四边形,DE平分∠ADC交AB于点E,BF平分∠ABC交CD于点F.(1)求证DE=BF;(2)连接EF,写出图中所有的全等三角形.(不要求证明)证明:(1)∵四边形ABCD是平行四边形,∴DC∥AB,∴∠CDE=∠AED.∵DE平分∠ADC,∴∠ADE=∠CDE,∴∠ADE=∠AED,∴AE=AD.同理CF=CB.又AD=CB,∴CF=AE,∴DF=BE,∴四边形DEBF是平行四边形,∴DE=BF.解:(2)△ADE≌△CBF,△DFE≌△BEF.