人教版八年级物理上册第六章测试题（含答案） 8页

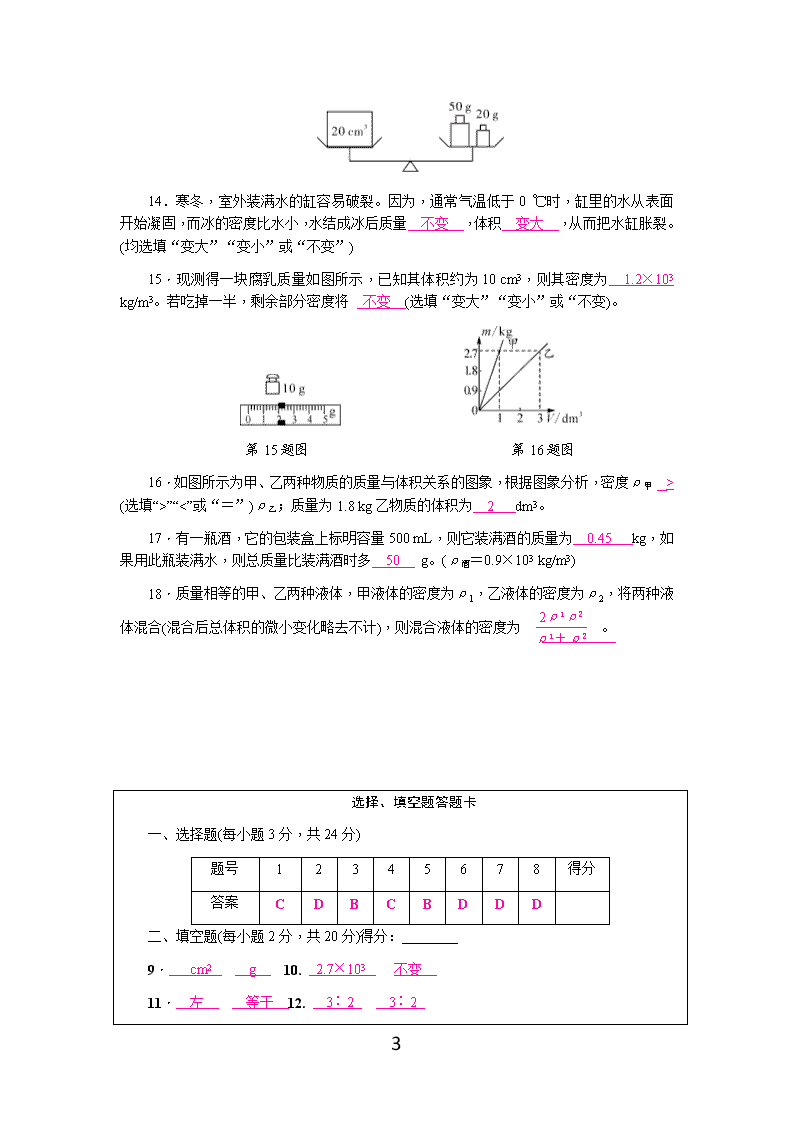
人教版八年级物理上册第六章测试题（含答案）‎ ‎(时间：90分钟　　满分：100分)‎ 一、选择题(本大题共8个小题，每小题只有一个正确选项，每小题3分，共24分)‎ ‎1．2020年2月3日，黑龙江省人民把3吨抗疫物资从哈尔滨用飞机运送到武汉，到达武汉后抗疫物资的质量( C )‎ A.增大　　　　　　　 B．减小 C．不变 D．无法确定 ‎2．椰子是大自然对海南的美好馈赠。一个成熟饱满的椰子质量最接近( D )‎ A.2 g　　　 B．20 g　　 C．200 g　　 D．2 000 g ‎3．在“用托盘天平称物体的质量”的实验中，下列操作错误的是( B )‎ A.使用天平时，将天平放在水平桌面上 B．调节横梁平衡时，只调节了平衡螺母 C．称量时，左盘放置待测物体，右盘放置砝码 D．观察到指针指在分度盘的中线处，确定天平已平衡 ‎4．5月20日是世界计量日，2019年的主题是“国际单位制(SI)——本质的提升”。在国际单位制中，密度单位的国际符号是( C )‎ A.kg/dm3 B．m/s C．kg/m3 D．g/cm3‎ ‎5．在食用油、酱油、白酒和水这几种常见液体中，密度最大的是( B )‎ A.食用油 B．酱油 C．白酒 D．水 ‎6．水是一种资源，也是一种能源。古代劳动人民巧妙地利用水来开山采石。冬季，在白天给石头打一个洞，再往洞里灌满水并封实，待晚上降温，水结冰后石头就裂开了(冰的密度比水的小)。下列有关说法正确的是( D )‎ A.石头裂开后密度减小 B．石头裂开后密度增大 C．该方法利用水结冰后质量变大，体积增大而使石头裂开 D．该方法利用水结冰后质量不变，体积增大而使石头裂开 ‎7．某同学用托盘天平和量筒测量一小石块的密度，图甲是调节天平时的情形，图乙和图丙分别是测量石块质量和体积时的情形，下列说法中正确的是( D )‎ 8‎ A．甲图中应将平衡螺母向左调，使横梁平衡 B．乙图中测石块质量时，天平的示数是17.4 g C．由丙图量筒的示数测得石块的体积是40 cm3‎ D．利用图中信息，可计算出石块的密度是1.72×103 kg/m3‎ ‎8．下列关于质量和体积都相同的铅球、铝球和铁球的说法不正确的是(ρ铅>ρ铁>ρ铝)( D )‎ A.三球中至少有两球是空心的 B．三个球如果都是空心的，则空心注满水后，铅球的质量最大 C．铅球和铁球一定是空心的 D．铅球和铁球如果是空心的，在空心注满不同的液体后，两球的质量如果相等，则注入的两种液体的密度一定相等 二、填空题(本大题共10个小题，每小题2分，共20分)‎ ‎9．智能手机是我们常见的通讯工具，请你估测一下：手机屏幕的面积大约为80 cm2 ，手机的质量大约为200 g 。(填写合适单位的符号)‎ ‎10．一物体的质量是2.7×104 kg，体积为10 m3，则其密度为 2.7×103 kg/m3。若把该物体切去一半，则剩下部分的密度将 不变 (选填“变大”“变小”或“不变”)。‎ ‎11．学过天平使用的知识后，好奇的小明想用家中的一架旧天平称一个鸡蛋的质量。在调节横梁平衡时，先将游码移至零刻度线处，此时指针偏向分度盘右侧，则应将平衡螺母向左 调节。他发现无论怎样调节平衡螺母，指针总略偏向分度盘右侧，于是他在天平的左盘中放入几粒米后重新调节平衡并进行了测量，如图所示，则鸡蛋的质量 等于 (选填“大于”“等于”或“小于”)61 g。‎ ‎12．体积相同的甲、乙两物体的质量之比为3∶2，则甲、乙两物体的密度之比为 3∶2 ，如果把甲、乙两物体都截去一半，两物体剩余部分的密度之比为 3∶2 。‎ ‎13．如图所示，天平处于平衡状态。则左盘物块的密度是 3.5 g/cm3 。‎ 8‎ ‎14．寒冬，室外装满水的缸容易破裂。因为，通常气温低于0 ℃时，缸里的水从表面开始凝固，而冰的密度比水小，水结成冰后质量 不变 ，体积 变大 ，从而把水缸胀裂。(均选填“变大”“变小”或“不变”)‎ ‎15．现测得一块腐乳质量如图所示，已知其体积约为10 cm3，则其密度为 1.2×103 kg/m3。若吃掉一半，剩余部分密度将 不变 (选填“变大”“变小”或“不变)。‎ ‎ ‎ 第15题图　 　第16题图 ‎16．如图所示为甲、乙两种物质的质量与体积关系的图象，根据图象分析，密度ρ甲 > (选填“>”“<”或“＝”)ρ乙；质量为1.8 kg乙物质的体积为 2 dm3。‎ ‎17．有一瓶酒，它的包装盒上标明容量500 mL，则它装满酒的质量为 0.45 kg，如果用此瓶装满水，则总质量比装满酒时多 50 g。(ρ酒＝0.9×103 kg/m3)‎ ‎18．质量相等的甲、乙两种液体，甲液体的密度为ρ1，乙液体的密度为ρ2，将两种液体混合(混合后总体积的微小变化略去不计)，则混合液体的密度为 。‎ 选择、填空题答题卡 一、选择题(每小题3分，共24分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 得分 答案 C D B C B D D D 二、填空题(每小题2分，共20分)得分：________‎ ‎9． cm2 　 g 　10. 2.7×103 　不变 ‎ ‎11． 左　 等于　12. 3∶2 　3∶2 ‎ 8‎ ‎13． 3.5 g/cm3 14. 不变 　变大 ‎ ‎15． 1.2×103 　不变 ‎16． >　 2 17. 0.45 　50 ‎ ‎18. ‎ 三、实验、探究题(本大题共4个小题，共31分)‎ ‎19．(4分)如图甲，是某地质公园的“玄武石”，其内部是多孔蜂窝状结构，该类石头的密度为2.8～3.3 g/cm3。小明想准确测出这块石头的密度。‎ ‎　‎ ‎(1)如图乙，该石头的质量为 52.4 g；他将该石头放入量筒中，液面位置如图丙所示，计算得到该石头的密度为 2.62 g/cm3。‎ ‎(2)该石头密度的测量值偏 大 ，原因是： 石头多孔，测得的体积偏小 。‎ ‎20．(8分)在“测量石块的密度”实验中：‎ ‎(1)小李同学首先用天平测出石块的质量，天平平衡时右盘砝码和游码位置如图甲所示，则石块的质量为 43 g。‎ ‎(2)为了测量出石块的体积，小李同学先往量筒中加入一定量的水，如图乙所示，他的操作合理吗？为什么？‎ 答：不合理，水太多，石块浸没后，总体积会超过量筒的量程。‎ ‎(3)四个小组测量出的石块密度如表所示：‎ 第一组 ‎2.5×103 kg/m3‎ 第二组 ‎2.6 g/cm3‎ 8‎ 第三组 ‎2.6×102 kg/m3‎ 第四组 ‎2.5 g/cm3‎ 其中错误的是第 三 组的测量结果。‎ ‎(4)对实验进行评估时，下列分析正确的是 D 。‎ A．放置天平的操作台面不水平，测出的质量偏大 B．放置天平的操作台面不水平，测出的质量偏小 C．先测石块体积，后测石块质量，测出的密度偏小 D．先测石决体积，后测石块质量，测出的密度偏大 ‎21．(5分)(甘肃中考)学完质量和密度后，小明和小军利用托盘天平和量筒测某种油的密度。‎ ‎(1)他们把天平放在水平桌面上，当游码移至零刻度线处时，指针偏向分度盘的右侧。这时他们应将平衡螺母向 左 (选填“左”或“右”)调，使横梁平衡；‎ ‎(2)天平平衡后，他们开始测量，测量步骤如下：‎ A．用天平测出烧杯和剩余油的总质量；‎ B．将待测油倒入烧杯中，用天平测出烧杯和油的总质量；‎ C．将烧杯中油的一部分倒入量筒，测出倒出到量筒的这部分油的体积。‎ 请根据以上步骤，写出正确的操作顺序： BCA (填字母代号)；‎ ‎(3)若在步骤B中测得烧杯和油的总质量为55.8 g，其余步骤数据如图所示，则倒出到量筒的这部分油的质量是 18.4 g，体积是 20 cm3；‎ ‎(4)根据密度的计算公式可以算出，该油的密度是 0.92×103 kg/m3。‎ ‎22．(14分)今年小明家乡种植的杏获得了丰收，他想利用托盘天平和量筒测量一颗鲜杏的密度，进行了下列操作：‎ 8‎ ‎(1)先把天平放在水平台上，然后将游码移至标尺左端的零刻度线处，为使天平横梁平衡，他应该调节横梁右端的 平衡螺母 ；‎ ‎(2)将鲜杏放在调好的天平左盘，天平平衡时右盘中的砝码和游码位置如图甲所示，则鲜杏的质量为 21.2 g；‎ ‎(3)为了能将鲜杏放入量筒，小明选取了容积为200 mL的量筒，他先往量筒中加入适量的水，记下此时水的体积，如图乙所示；再将这个鲜杏放入量筒，再次记录读数，请你帮他计算鲜杏的密度为 1.06× 103 kg/m3；‎ ‎(4)小明继续实验时不小心将量筒碰倒摔碎了，他又选取了小烧杯、溢水杯，容积为50 mL的量筒测量鲜杏的体积，他的做法如下，请你将下列步骤补充完整。‎ a．先将溢水杯中盛满水，再将鲜杏轻轻放入溢水杯中，让溢出的水流入小烧杯中；‎ b． 将小烧杯中的水全部倒入量筒 ；‎ c．记录此时量筒中水的体积。‎ 你认为小明按上述做法测出的鲜杏密度比真实值 偏大 (选填“偏大”或“偏小”)，其原因是 小烧杯中的水未倒尽，杯壁有残留，所测鲜杏的体积会偏小，所测鲜杏的质量一定，由密度公式ρ＝可知所测鲜杏的密度偏大 。‎ 四、综合题(本大题共3个小题，共25分)‎ 要求：(1)语言表述要简练、准确；(2)写出必要的运算和推理过程；(3)带单位计算；(4)计算结果若有近似，均保留两位小数。‎ ‎23．(7分)一个体积是30 cm3的空心铜球质量是89 g，将它的中空部分注满某种液体物质后，总质量是361 g，已知铜的密度为8.9 g/cm3，那么注入液体的密度是多少？‎ 解：由ρ＝可得，‎ 铜球中含铜的体积：V铜＝＝＝10 cm3，‎ 注入液体的体积：‎ V液＝V球－V铜＝30 cm3－10 cm3＝20 cm3，‎ 8‎ 注入液体的质量：‎ m液＝m总－m球＝361 g－89 g＝272 g，‎ 注入液体的密度为：‎ ρ液＝＝＝13.6 g/cm3。‎ ‎24．(8分)奖牌分为金牌、银牌和铜牌。其中金牌由纯银、玉石、纯金组成，金牌的总体积约为23 cm3，镶嵌玉石的体积约为5 cm3，纯金的质量约为6 g。已知ρ玉＝3 g/cm3，ρ金＝19 g/cm3，ρ银＝10 g/cm3。‎ ‎(1)一枚金牌约需玉石多少克？‎ ‎(2)一枚金牌除玉石和纯金外，还需纯银约多少克？‎ 解：(1)由ρ＝可得，金牌中玉石的质量：‎ m玉＝ρ玉V玉＝3 g/cm3×5 cm3＝15 g；‎ ‎(2)金牌中金的体积：‎ V金＝＝≈0.3 cm3，‎ 金牌中银的体积：V银＝V总－V玉－V金＝23 cm3－5 cm3－0.3 cm3＝17.7 cm3，‎ 金牌中银的质量：‎ m银＝ρ银V银＝10 g/cm3×17.7 cm3＝177 g。‎ ‎25．(10分)某品牌自行车的质量为34.2 kg，其中橡胶占总体积的，其余部分为钢材。已知自行车所有钢材质量为31.6 kg，已知ρ钢＝7.9×103 kg/m3。‎ ‎(1)橡胶的密度是多少？‎ ‎(2)若将所用的钢材换为密度为4 g/cm3的某合金材料，则自行车的质量为多少？‎ 8‎ 解：(1)由ρ＝可得，钢材的体积：‎ V钢＝＝＝4×10－3 m3，‎ 则自行车的总体积 V＝＝＝6×10－3 m3，‎ 橡胶的质量：‎ m橡胶＝m－m钢＝34.2 kg－31.6 kg＝2.6 kg，‎ 橡胶的体积：V橡胶＝V＝×6×10－3 m3＝2×10－3 m3，‎ 则橡胶的密度：ρ橡胶＝＝＝1.3×103 kg/m3，‎ ‎(2)若将所用的钢材换为合金材料，其质量为：m合金＝ρ合金V钢＝4×103 kg/m3×4×10－3 m3＝16 kg，‎ 则自行车的质量 m′＝m合金＋m橡胶＝16 kg＋2.6 kg＝18.6 kg。‎ 8‎