- 377.55 KB
- 2021-10-26 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2019-2020学年山东省济南市章丘区八年级(下)期末数学试卷
一.选择题(本大题共12小题,每小题4分,共48分.在每个小题给出四个选项中只有一项符合题目要求)
1. 若a>b,则下列各式中一定成立的是( )
A.a+2b2 D.−2a>−2b
2. 在下列因式分解的过程中,分解因式正确的是( )
A.x2+2x+4=(x+2)2 B.x2−4=(x+4)(x−4)
C.x2−4x+4=(x−2)2 D.x2+4=(x+2)2
3. 垃圾分类功在当代利在千秋,下列垃圾分类指引标志图形中,是轴对称图形又是中心对称图形的是( )
A.厨余垃圾FoodWaste
B.可回收物Recyclable
C.其他垃圾ResidualWaste
D.有害垃圾HazardousWaste
4. 若式子x−1x−2在实数范围内有意义,则x的取值范围是( )
A.x≥1且x≠2 B.x≤1 C.x>1且x≠2 D.x<1
5. 如图,在平面直角坐标系xOy中,已知点A(2, 1),点B(3, −1).平移线段AB,使点A落在点A1(−2, 2)处,则点B的对应点B1的坐标为( )
A.(−1, −1) B.(−1, 0) C.(1, 0) D.(3, 0)
6. 如图,三条公路把A、B、C三个村庄连成一个三角形区域,某地区决定在这个三角形区域内修建一个集贸市场,要使集贸市场到三个条公路的距离相等,则这个集贸市场应建在( )
A.在AC、BC两边高线的交点处
B.在AC、BC两边中线的交点处
C.在∠A、∠B两内角平分线的交点处
D.在AC、BC两边垂直平分线的交点处
7. 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解集为( )
A.x>−1 B.x<−1 C.x<−2 D.x>−2
8. 下列说法不正确的是( )
A.平行四边形的对边平行且相等
B.平行四边形对角线互相平分
C.平行四边形既是轴对称图形又是中心对称图形
D.两组对角分别相等的四边形是平行四边形
第21页 共24页 ◎ 第22页 共24页
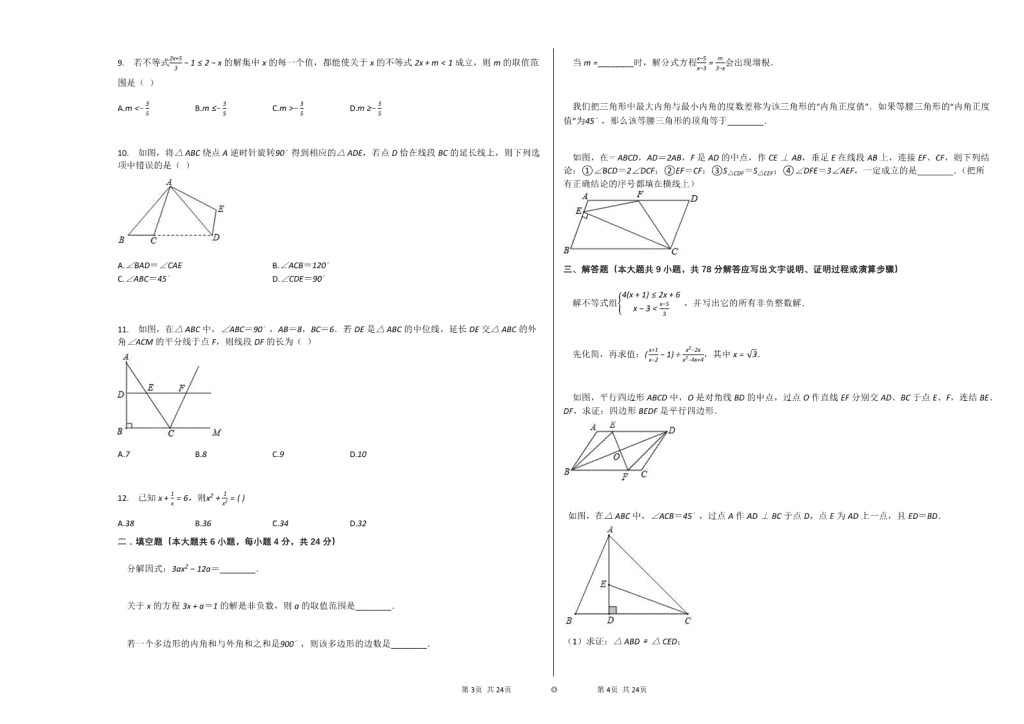
9. 若不等式2x+53−1≤2−x的解集中x的每一个值,都能使关于x的不等式2x+m<1成立,则m的取值范围是( )
A.m<−35 B.m≤−35 C.m>−35 D.m≥−35
10. 如图,将△ABC绕点A逆时针旋转90∘得到相应的△ADE,若点D恰在线段BC的延长线上,则下列选项中错误的是( )
A.∠BAD=∠CAE B.∠ACB=120∘
C.∠ABC=45∘ D.∠CDE=90∘
11. 如图,在△ABC中,∠ABC=90∘,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
A.7 B.8 C.9 D.10
12. 已知x+1x=6,则x2+1x2=( )
A.38 B.36 C.34 D.32
二.填空题(本大题共6小题,每小题4分,共24分)
分解因式:3ax2−12a=________.
关于x的方程3x+a=1的解是非负数,则a的取值范围是________.
若一个多边形的内角和与外角和之和是900∘,则该多边形的边数是________.
当m=________时,解分式方程x−5x−3=m3−x会出现增根.
我们把三角形中最大内角与最小内角的度数差称为该三角形的“内角正度值”.如果等腰三角形的“内角正度值”为45∘,那么该等腰三角形的顶角等于________.
如图,在▱ABCD,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:①∠BCD=2∠DCF;②EF=CF;③S△CDF=S△CEF;④∠DFE=3∠AEF,一定成立的是________.(把所有正确结论的序号都填在横线上)
三、解答题(本大题共9小题,共78分解答应写出文字说明、证明过程或演算步骤)
解不等式组4(x+1)≤2x+6x−3<x−53 ,并写出它的所有非负整数解.
先化简,再求值:(x+1x−2−1)÷x2−2xx2−4x+4,其中x=3.
如图,平行四边形ABCD中,O是对角线BD的中点,过点O作直线EF分别交AD、BC于点E、F,连结BE、DF,求证:四边形BEDF是平行四边形.
如图,在△ABC中,∠ACB=45∘,过点A作AD⊥BC于点D,点E为AD上一点,且ED=BD.
(1)求证:△ABD≅△CED;
第21页 共24页 ◎ 第22页 共24页
(2)若CE为∠ACD的角平分线,求∠BAC的度数.
阅读下面的材料:
常用的分解因式的方法有提取公因式法,公式法等,但有的多项式只用上述方法无法分解.如x2−4y2−2x+4y,细心观察这个式子,会发现前两项符合平方差公式,后两项可提取公因式,前、后两部分分别因式分解后又出现新的公因式,提取公因式就可以完成整个式子的分解因式.具体过程如下:
x2−4y2−2x+4y
=(x2−4y2)−(2x−4y)
=(x+2y)(x−2y)−2(x−2y)
=(x−2y)(x+2y−2)
像这种将一个多项式适当分组后,进行分解因式的方法叫做分组分解法.
利用分组分解法解决下面的问题:
(1)分解因式:x2−2xy+y2−4;
(2)已知△ABC的三边长a,b,c满足a2−ab−ac+bc=0,判断△ABC的形状并说明理由.
如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点分别为A(−2, 2),B(0, 5),C(0, 2).
(1)画△A1B1C1,使它与△ABC关于点C成中心对称,则B1的坐标为________;
(2)平移△ABC,使点A的对应点A2的坐标为(−4, −6),画出平移后对应的△A2B2C2,则B2的坐标为________;
(3)若将△A1B1C1绕某一点旋转可得到△A2B2C2,则旋转中心的坐标为________.
复课返校后,为了拉大学生锻炼的间距,某学校决定增购适合独立训练的两种体育器材:跳绳和毽子,已知跳绳的单价比毽子的单价多4元,用1000元购买的跳绳个数和用800元购买的键子数量相同.
(1)求跳绳和毽子的单价分别是多少元?
(2)学校计划购买跳绳和毽子两种器材共400个,由于受疫情影响,商场决定对这两种器材打折销售,其中跳绳以八折出售,毽子以七五折出售,学校要求跳绳的数量不少于毽子数量的3倍,跳绳的数量不多于310根,请你求出学校花钱最少的购买方案.
如图1,在Rt△ABC中,AB=AC,∠A=90∘,点D、E分别在边AB、AC上,AD=AE,连结DC,点M、P、N分别为DE、DC、BC的中点.
(1)观察猜想:
图1中,线段PM与PN的数量关系是________,位置关系是________;
(2)探究证明:
把△ADE绕点A逆时针方向旋转到图2的位置,连结MN,判断△PMN的形状,并说明理由;
(3)拓展延伸:
把△ADE绕点A在平面内自由旋转,若DE=2,BC=4,请直接写出△PMN面积的最大值.
在平面直角坐标系xOy中,已知点A (1, 1),B (3, 2).
(1)如图1,在y轴上是否存在一点P,使PA+PB最小,若存在求出点P的坐标;若不存在,请说明理由.
第21页 共24页 ◎ 第22页 共24页
(2)如图2,点C坐标为(4, 1),点D由原点O沿x轴正方向以每秒1个单位的速度运动,求点D运动几秒时,四边形ABCD是平行四边形;
(3)点P在x轴上,点Q在y轴上,且以A、B、P、Q为顶点的四边形是平行四边形,请直接写出点P以及对应的点Q的坐标.
第21页 共24页 ◎ 第22页 共24页
参考答案与试题解析
2019-2020学年山东省济南市章丘区八年级(下)期末数学试卷
一.选择题(本大题共12小题,每小题4分,共48分.在每个小题给出四个选项中只有一项符合题目要求)
1.
【答案】
C
【考点】
不等式的性质
【解析】
根据不等式的性质即可求出答案.
【解答】
解:A,a+2>b+2,故A错误;
B,a−2>b−2,故B错误;
C,a2>b2,故C正确;
D,−2a<−2b,故D错误.
故选C.
2.
【答案】
C
【考点】
提公因式法与公式法的综合运用
【解析】
各项分解得到结果,即可作出判断.
【解答】
A、原式不能分解,不符合题意;
B、原式=(x+2)(x−2),不符合题意;
C、原式=(x−2)2,符合题意;
D、原式不能分解,不符合题意,
3.
【答案】
D
【考点】
中心对称图形
轴对称图形
【解析】
根据轴对称图形与中心对称图形的概念求解.
【解答】
A、是轴对称图形,不是中心对称图形,故此选项不符合题意;
B、不是轴对称图形,不是中心对称图形,故此选项不符合题意;
C、不是轴对称图形,不是中心对称图形,故此选项不符合题意;
D、是轴对称图形,也是中心对称图形,故此选项符合题意.
4.
【答案】
A
【考点】
分式有意义、无意义的条件
二次根式有意义的条件
【解析】
分式有意义,分母不等于零;二次根式的被开方数是非负数.
【解答】
解:式子x−1x−2在实数范围内有意义,得
x−1≥0且x−2≠0,
解得x≥1且x≠2.
故选A.
5.
【答案】
B
【考点】
坐标与图形变化-平移
【解析】
利用平移变换的性质画出图形解决问题即可.
【解答】
如图,B1(−1, 0),
6.
【答案】
C
【考点】
角平分线的性质
【解析】
根据角平分线上的点到角的两边的距离相等解答即可.
【解答】
根据角平分线的性质,集贸市场应建在∠A、∠B两内角平分线的交点处.
7.
【答案】
B
【考点】
第21页 共24页 ◎ 第22页 共24页
一次函数与一元一次不等式
【解析】
根据图象利用一次函数与一元一次不等式的关系即可求解.
【解答】
由图象知:x的不等式k1x+b>k2x的解集为x<−1,
8.
【答案】
C
【考点】
轴对称图形
中心对称图形
平行四边形的性质与判定
【解析】
分别根据平行四边形的性质与定义逐一判断即可.
【解答】
A.平行四边形的对边平行且相等,说法正确,故本选项不合题意;
B.平行四边形对角线互相平分,说法正确,故本选项不合题意;
C.平行四边形是中心对称图形,不是轴对称图形,故原说法错误,故本选项符合题意;
D.两组对角分别相等的四边形是平行四边形说法正确,故本选项不合题意.
9.
【答案】
A
【考点】
解一元一次不等式
【解析】
求出不等式2x+53−1≤2−x的解,求出不等式3(x−1)+5>5x+2(m+x)的解集,得出关于m的不等式,求出m即可.
【解答】
解不等式2x+53−1≤2−x得:x≤45,
∵ 不等式2x+53−1≤2−x的解集中x的每一个值,都能使关于x的不等式2x+m<1成立,
∴ x<1−m2,
∴ 1−m2>45,
解得:m<−35,
10.
【答案】
B
【考点】
旋转的性质
【解析】
根据旋转的性质和等腰直角三角形的判定和性质定理即可得到结论.
【解答】
∵ 将△ABC绕点A逆时针旋转90∘得到相应的△ADE,
∴ ∠BAD=∠CAE=90∘,AB=AD,∠ABC=∠ADE,
∴ ∠ABC=∠ADB=45∘,
∴ ∠ADE=45∘,
∴ ∠CDE=90∘,
得不到∠ACB=120∘,
故A,C,D正确,B错误,
11.
【答案】
B
【考点】
等腰三角形的判定与性质
勾股定理
三角形中位线定理
【解析】
根据三角形中位线定理求出DE,得到DF // BM,再证明EC=EF=12AC,由此即可解决问题.
【解答】
解:在RT△ABC中,∵ ∠ABC=90∘,AB=8,BC=6,
∴ AC=AB2+BC2=82+62=10,
∵ DE是△ABC的中位线,
∴ DF // BM,DE=12BC=3,
∴ ∠EFC=∠FCM,
∵ ∠FCE=∠FCM,
∴ ∠EFC=∠ECF,
∴ EC=EF=12AC=5,
∴ DF=DE+EF=3+5=8.
故选B.
12.
【答案】
C
【考点】
完全平方公式
【解析】
此题考查了完全平方公式.
【解答】
第21页 共24页 ◎ 第22页 共24页
解:把x+1x=6两边平方得:(x+1x)2=x2+1x2+2=36,
则x2+1x2=34,
故选C.
二.填空题(本大题共6小题,每小题4分,共24分)
【答案】
3a(x+2)(x−2)
【考点】
提公因式法与公式法的综合运用
【解析】
原式提取公因式,再利用平方差公式分解即可.
【解答】
原式=3a(x2−4)
=3a(x+2)(x−2).
【答案】
a≤1
【考点】
解一元一次不等式
一元一次方程的解
【解析】
首先要解这个关于x的方程,然后根据解是非负数,就可以得到一个关于a的不等式,最后求出a的取值范围.
【解答】
方程3x+a=1,
解得:x=1−a3,
∵ 关于x的方程3x+a=1的解是非负数,
∴ 1−a3≥0,
解得:a≤1.
【答案】
5
【考点】
多边形内角与外角
【解析】
本题需先根据已知条件以及多边形的外角和是360∘,解出内角和的度数,再根据内角和度数的计算公式即可求出边数.
【解答】
∵ 多边形的内角和与外角和的总和为900∘,多边形的外角和是360∘,
∴ 多边形的内角和是900−360=540∘,
∴ 多边形的边数是:540∘÷180∘+2=3+2=5.
【答案】
2
【考点】
分式方程的增根
【解析】
此题暂无解析
【解答】
解:分式方程可化为:x−5=−m,
由分母可知,分式方程的增根是3,
当x=3时,3−5=−m,解得m=2,
故答案为:2.
【答案】
90∘或30∘
【考点】
等腰三角形的性质
【解析】
本题主要考查了等腰三角形的性质.
【解答】
解:设最小角为x,则最大角为x+45∘,
当最小角是顶角时,则x+x+45∘+x+45∘=180∘,
解得x=30∘,
当最大角为顶角时,x+x+45∘+x=180∘,
解得x=45∘,
即等腰三角形的顶角为30∘或90∘,
故答案为:30∘或90∘.
【答案】
①②④
【考点】
平行四边形的性质
直角三角形斜边上的中线
全等三角形的性质与判定
【解析】
分别利用平行四边形的性质以及全等三角形的判定,即可得出△AEF≅△DMF(ASA),得出对应线段之间关系进而得出答案.
【解答】
①∵ F是AD的中点,
∴ AF=FD,
∵ 在▱ABCD中,AD=2AB,
∴ AF=FD=CD,
∴ ∠DFC=∠DCF,
∵ AD // BC,
∴ ∠DFC=∠FCB,
∴ ∠DCF=∠BCF,
∴ 2∠DCF=∠BCD,故①正确;
如图,延长EF,交CD延长线于M,
∵ 四边形ABCD是平行四边形,
∴ AB // CD,
∴ ∠A=∠MDF,
∵ F为AD中点,
∴ AF=FD,
在△AEF和△DFM中,
∠A=∠FDMAF=DF∠AFE=∠DFM ,
∴ △AEF≅△DMF(ASA),
∴ FE=MF,∠AEF=∠M,
∵ CE⊥AB,
∴ ∠AEC=90∘,
∴ ∠AEC=∠ECD=90∘,
∵ FM=EF,
∴ FC=FE=FM,故②正确;
第21页 共24页 ◎ 第22页 共24页
③∵ EF=FM,
∴ S△EFC=S△CFM,
∵ MC>DC,
∴ S△CDF<S△CFM,
故S△CDF=S△CEF不成立,故③错误;
④设∠FEC=x,则∠FCE=x,
∴ ∠DCF=∠DFC=90∘−x,
∴ ∠EFC=180∘−2x,
∴ ∠EFD=90∘−x+180∘−2x=270∘−3x,
∵ ∠AEF=90∘−x,
∴ ∠DFE=3∠AEF,故此选项正确.
三、解答题(本大题共9小题,共78分解答应写出文字说明、证明过程或演算步骤)
【答案】
解不等式4(x+1)≤2x+6,得:x≤1,
解不等式x−3<x−53,得:x<2,
则不等式组的解集为x≤1,
所以不等式组的非负整数解为0、1.
【考点】
解一元一次不等式组
一元一次不等式组的整数解
【解析】
分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集,从而得出答案.
【解答】
解不等式4(x+1)≤2x+6,得:x≤1,
解不等式x−3<x−53,得:x<2,
则不等式组的解集为x≤1,
所以不等式组的非负整数解为0、1.
【答案】
解:原式=(x+1x−2−x−2x−2)÷x(x−2)(x−2)2
=3x−2⋅x−2x
=3x,
当x=3时,原式=33=3.
【考点】
分式的化简求值
【解析】
先根据分式的混合运算顺序和运算法则化简原式,再将x的值代入计算可得.
【解答】
解:原式=(x+1x−2−x−2x−2)÷x(x−2)(x−2)2
=3x−2⋅x−2x
=3x,
当x=3时,原式=33=3.
【答案】
证明:∵ ABCD是平行四边形,O是对角线BD的中点,
∴ OB=OD,DE // BF,
∴ ∠EDO=∠FOB,∠EOD=∠FOB,
∴ △DOE≅△BOF,
∴ OE=OF,
∴ 四边形DEBF是平行四边形.
【考点】
平行四边形的性质与判定
【解析】
只要证明OB=OD,O=OF即可解决问题.
【解答】
证明:∵ ABCD是平行四边形,O是对角线BD的中点,
∴ OB=OD,DE // BF,
∴ ∠EDO=∠FOB,∠EOD=∠FOB,
∴ △DOE≅△BOF,
∴ OE=OF,
∴ 四边形DEBF是平行四边形.
【答案】
证明:∵ AD⊥BC,∠ACB=45∘,
∴ ∠ADB=∠CDE=90∘,△ADC是等腰直角三角形,
∴ AD=CD,∠CAD=∠ACD=45∘,
在△ABD与△CED中,AD=CD∠ADB=∠CDEBD=ED ,
∴ △ABD≅△CED(SAS);
第21页 共24页 ◎ 第22页 共24页
∵ CE为∠ACD的角平分线,
∴ ∠ECD=12∠ACD=22.5∘,
由(1)得:△ABD≅△CED,
∴ ∠BAD=∠ECD=22.5∘,
∴ ∠BAC=∠BAD+∠CAD=22.5∘+45∘=67.5∘.
【考点】
全等三角形的性质与判定
【解析】
(1)证出△ADC是等腰直角三角形,得出AD=CD,∠CAD=∠ACD=45∘,由SAS证明△ABD≅△CED即可;
(2)由角平分线定义得出∠ECD=12∠ACD=22.5∘,由全等三角形的性质得出∠BAD=∠ECD=22.5∘,即可得出答案.
【解答】
证明:∵ AD⊥BC,∠ACB=45∘,
∴ ∠ADB=∠CDE=90∘,△ADC是等腰直角三角形,
∴ AD=CD,∠CAD=∠ACD=45∘,
在△ABD与△CED中,AD=CD∠ADB=∠CDEBD=ED ,
∴ △ABD≅△CED(SAS);
∵ CE为∠ACD的角平分线,
∴ ∠ECD=12∠ACD=22.5∘,
由(1)得:△ABD≅△CED,
∴ ∠BAD=∠ECD=22.5∘,
∴ ∠BAC=∠BAD+∠CAD=22.5∘+45∘=67.5∘.
【答案】
x2−2xy+y2−4
=(x−y)2−4
=(x−y+2)(x−y−2)
∵ a2−ab−ac+bc=0,
∴ a(a−b)−c(a−b)=0,
∴ (a−b)(a−c)=0,
∴ a−b=0或a−c=0,
∴ a=b或a=c,
∴ △ABC是等腰三角形.
【考点】
因式分解的应用
【解析】
(1)前三项符合完全平方公式,再和最后一项应用平方差公式分解因式即可.
(2)前两项、后两项均可提取公因式,前、后两部分分别因式分解后又出现新的公因式,据此把a2−ab−ac+bc分解因式,进而判断出△ABC的形状即可.
【解答】
x2−2xy+y2−4
=(x−y)2−4
=(x−y+2)(x−y−2)
∵ a2−ab−ac+bc=0,
∴ a(a−b)−c(a−b)=0,
∴ (a−b)(a−c)=0,
∴ a−b=0或a−c=0,
∴ a=b或a=c,
∴ △ABC是等腰三角形.
【答案】
(0, −1)
(−2, −3)
(−1, −2)
【考点】
作图-相似变换
作图-旋转变换
【解析】
(1)分别作出A,B的对应点A1,B1即可.
(2)分别作出A,B,C的对应点A2,B2,C2即可.
(3)对应点连线段的交点即为旋转中心.
【解答】
如图△A1B1C1即为所求,B1的坐标为(0, −1).
故答案为(0, −1).
△A2B2C2即为所求,则B2的坐标为(−2, −3).
故答案为(−2, −3).
如图旋转中心为点P,P(−1, −2).
故答案为(−1, −2).
【答案】
跳绳的单价为20元,毽子的单价为16元
当学校购买300根跳绳、100个毽子时,总费用最少
【考点】
分式方程的应用
一元一次不等式组的应用
【解析】
(1)设毽子的单价为x元,则跳绳的单价为(x+4)元,根据数量=总价÷单价结合用1000元购买的跳绳个数和用800元购买的键子数量相同,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设购买毽子m个,则购买跳绳(400−m)根,根据跳绳的数量不少于毽子数量的3倍且跳绳的数量不多于310
第21页 共24页 ◎ 第22页 共24页
根,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,设学校购买跳绳和毽子两种器材共花w元,根据总价=单价×数量可得出w关于m的函数关系式,再利用一次函数的性质即可解决最值问题.
【解答】
设毽子的单价为x元,则跳绳的单价为(x+4)元,
依题意,得:1000x+4=800x,
解得:x=16,
经检验,x=16是原方程的解,且符合题意,
∴ x+4=20.
答:跳绳的单价为20元,毽子的单价为16元.
设购买毽子m个,则购买跳绳(400−m)根,
依题意,得:400−m≥3m400−m≤310 ,
解得:90≤m≤100.
设学校购买跳绳和毽子两种器材共花w元,则w=20×0.8(400−m)+16×0.75m=−4m+6400.
∵ −4<0,
∴ w随m的增大而减小,
∴ 当m=100时,w取得最小值,最小值=−4×100+6400=6000.
答:当学校购买300根跳绳、100个毽子时,总费用最少.
【答案】
PM=PN,PM⊥PN
的方法得,PM // CE,
∴ ∠DPM=∠DCE,
同
的方法得,PN // BD,
∴ ∠PNC=∠DBC,
∵ ∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,
∴ ∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC
=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC
=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵ ∠BAC=90∘,
∴ ∠ACB+∠ABC=90∘,
∴ ∠MPN=90∘,
∴ △PMN是等腰直角三角形;
(1)若DE=2,BC=4,
在Rt△ABC中,AB=AC,BC=4,
∴ AB=22BC=22,
同理:AD=2,
由(2)知,△PMN是等腰直角三角形,PM=PN=12BD,
∴ PM最大时,△PMN面积最大,
∴ 点D在BA的延长线上,
∴ BD=AB+AD=22+2=32,
∴ PM=322,
∴ S△PMN最大=12PM2=12×(322)2=94.
【考点】
几何变换综合题
【解析】
(1)利用三角形的中位线得出PM=CE,PN=12BD,进而判断出BD=CE,即可得出结论,再利用三角形的中位线得出PM // CE得出∠DPM=∠DCA,最后用互余即可得出结论;
(2)先判断出△ABD≅△ACE,得出BD=CE,同(1)的方法得出PM=12BD,PN=12BD,即可得出PM=PN,同(1)的方法即可得出结论;
(3)先判断出BD最大时,△PMN的面积最大,而BD最大是AB+AD=14,即可得出结论.
【解答】
(1)∵ 点P,N是BC,CD的中点,
∴ PN // BD,PN=12BD,
∵ 点P,M是CD,DE的中点,
∴ PM // CE,PM=12CE,
∵ AB=AC,AD=AE,
∴ BD=CE,
∴ PM=PN,
∵ PN // BD,
∴ ∠DPN=∠ADC,
∵ PM // CE,
∴ ∠DPM=∠DCA,
∵ ∠BAC=90∘,
∴ ∠ADC+∠ACD=90∘,
∴ ∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90∘,
∴ PM⊥PN,
【答案】
存在,理由:
作点A关于y轴的对称点A′(−1, 1),连接A′B交y轴于点P,则点P为所求点,
则PA+PB=PA′+PB=A′B
第21页 共24页 ◎ 第22页 共24页
为最小,
设直线A′B的表达式为y=kx+b,则1=−k+b2=3k+b ,解得k=14b=54 ,
故直线A′B的表达式为y=14x+54,
当x=0时,y=54,
故点P的坐标为(0, 54);
由点B、C的坐标同理可得,直线BC的表达式为y=−x+5,
当四边形ABCD是平行四边形时,则AD // BC,
故直线AD表达式中的k为−1,
设直线AD的表达式为y=−x+m,
将点A的坐标代入上式并解得:m=2,
故直线AD的表达式为y=−x+2,
当y=0时,x=2,故点D(2, 0);
同理可得:直线AB的表达式为y=12x+12、直线CD的表达式为y=12x−1,即两直线表达式中的k值相同,
∴ AB // CD,
而AD // BC,
故当D的坐标为(2, 0)时,四边形ABCD是平行四边形,
即点D的坐标为(2, 0);
设点P、Q的坐标分别为(x, 0)、(0, y),而点A、B的坐标分别为(1, 1)、(3, 2),
①当AB是边时,
点A向右平移2个单位向上平移1个单位得到点B,同样点P(Q)向右平移2个单位向上平移1个单位得到点Q(P),
故x±2=0且0±1=y,解得x=−2y=1 或x=2y=−1 ;
故点P以及对应的点Q的坐标分别为(−2, 0)、(0, 1)或(2, 0)、(0, −1);
②当AB是对角线时,
由中点公式得:12(1+3)=12(x+0)且12(1+2)=12(0+y),解得x=4y=3 ,
故点P以及对应的点Q的坐标分别为(4, 0)、(0, 3);
综上,点P以及对应的点Q的坐标分别为(−2, 0)、(0, 1)或(2, 0)、(0, −1)或(4, 0)、(0, 3).
【考点】
四边形综合题
【解析】
(1)作点A关于y轴的对称点A′(−1, 1),连接A′B交y轴于点P,则点P为所求点,进而求解;
(2)当四边形ABCD是平行四边形时,则AD // BC,进而求出直线AD的表达式为y=−x+2,即可求解;
(3)分AB是边、AB是对角线两种情况,利用图象平移和中点公式即可求解.
【解答】
存在,理由:
作点A关于y轴的对称点A′(−1, 1),连接A′B交y轴于点P,则点P为所求点,
则PA+PB=PA′+PB=A′B为最小,
设直线A′B的表达式为y=kx+b,则1=−k+b2=3k+b ,解得k=14b=54 ,
故直线A′B的表达式为y=14x+54,
当x=0时,y=54,
故点P的坐标为(0, 54);
由点B、C的坐标同理可得,直线BC的表达式为y=−x+5,
当四边形ABCD是平行四边形时,则AD // BC,
故直线AD表达式中的k为−1,
设直线AD的表达式为y=−x+m,
将点A的坐标代入上式并解得:m=2,
故直线AD的表达式为y=−x+2,
当y=0时,x=2,故点D(2, 0);
同理可得:直线AB的表达式为y=12x+12、直线CD的表达式为y=12x−1,即两直线表达式中的k值相同,
∴ AB // CD,
而AD // BC,
故当D的坐标为(2, 0)时,四边形ABCD是平行四边形,
即点D的坐标为(2, 0);
设点P、Q的坐标分别为(x, 0)、(0, y),而点A、B的坐标分别为(1, 1)、(3, 2),
①当AB是边时,
点A向右平移2个单位向上平移1个单位得到点B,同样点P(Q)向右平移2个单位向上平移1个单位得到点Q(P),
故x±2=0且0±1=y,解得x=−2y=1 或x=2y=−1 ;
故点P以及对应的点Q的坐标分别为(−2, 0)、(0, 1)或(2, 0)、(0, −1);
②当AB是对角线时,
由中点公式得:12(1+3)=12(x+0)且12(1+2)=12(0+y),解得x=4y=3 ,
故点P以及对应的点Q的坐标分别为(4, 0)、(0, 3);
综上,点P以及对应的点Q的坐标分别为(−2, 0)
第21页 共24页 ◎ 第22页 共24页
、(0, 1)或(2, 0)、(0, −1)或(4, 0)、(0, 3).
第21页 共24页 ◎ 第22页 共24页
相关文档
- 2020-2021学年人教版初二数学上册2021-10-2620页
- 2020年河北省石家庄市中考地理试卷2021-10-2612页
- 2020-2021学年人教版初二数学上册2021-10-2624页
- 四川省达州市2020年中考道德与法治2021-10-268页
- 部编版八年级历史上册期末复习专题2021-10-2636页
- 初中8年级物理教案:第14讲 期中考试2021-10-2638页
- 中考物理真题及答案,精选10套,高分2021-10-26109页
- 宁夏2020年中考道德与法治试题(解析2021-10-2611页
- 2020八年级道德与法治下册 第一单2021-10-262页
- 2018中考地理总复习专题分类攻略专2021-10-266页