北师大版数学八年级上册第7章《平行线的证明》单元检测题 5页

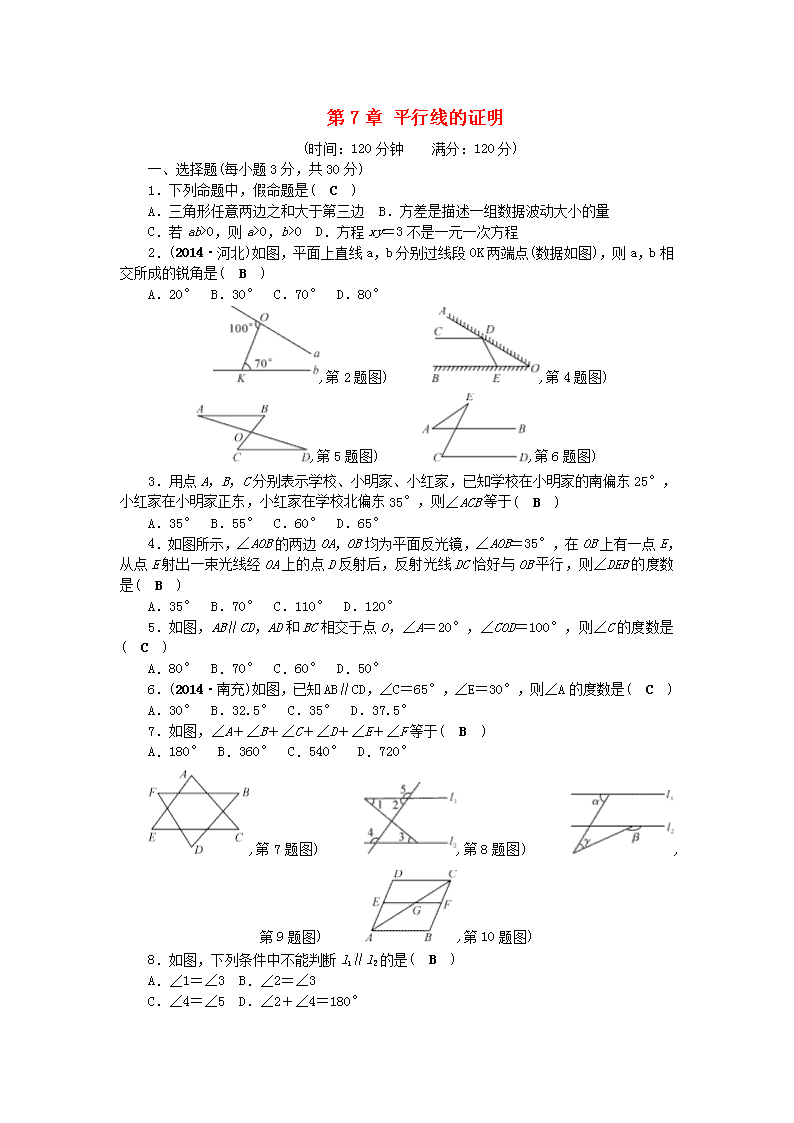
第 7 章 平行线的证明 (时间：120 分钟 满分：120 分) 一、选择题(每小题 3 分，共 30 分) 1．下列命题中，假命题是( C ) A．三角形任意两边之和大于第三边 B．方差是描述一组数据波动大小的量 C．若 ab>0，则 a>0，b>0 D．方程 xy＝3 不是一元一次方程 2．(2014·河北)如图，平面上直线 a，b 分别过线段 OK 两端点(数据如图)，则 a，b 相交所成的锐角是( B ) A．20° B．30° C．70° D．80° ,第 2 题图) ,第 4 题图) ,第 5 题图) ,第 6 题图) 3．用点 A，B，C 分别表示学校、小明家、小红家，已知学校在小明家的南偏东 25°， 小红家在小明家正东，小红家在学校北偏东 35°，则∠ACB 等于( B ) A．35° B．55° C．60° D．65° 4．如图所示，∠AOB 的两边 OA，OB 均为平面反光镜，∠AOB＝35°，在 OB 上有一点 E， 从点 E 射出一束光线经 OA 上的点 D 反射后，反射光线 DC 恰好与 OB 平行，则∠DEB 的度数 是( B ) A．35° B．70° C．110° D．120° 5．如图，AB∥CD，AD 和 BC 相交于点 O，∠A＝20°，∠COD＝100°，则∠C 的度数是( C ) A．80° B．70° C．60° D．50° 6．(2014·南充)如图，已知 AB∥CD，∠C＝65°，∠E＝30°，则∠A 的度数是( C ) A．30° B．32.5° C．35° D．37.5° 7．如图，∠A＋∠B＋∠C＋∠D＋∠E＋∠F 等于( B ) A．180° B．360° C．540° D．720° ,第 7 题图) ,第 8 题图) , 第 9 题图) ,第 10 题图) 8．如图，下列条件中不能判断 l1∥l2 的是( B ) A．∠1＝∠3 B．∠2＝∠3 C．∠4＝∠5 D．∠2＋∠4＝180° 9．如图，l1∥l2，下列式子中，等于 180°的是( B ) A．α＋β＋γ B．α＋β－γ C．－α＋β＋γ D．α－β＋γ 10．如图，AB∥CD∥EF，BC∥AD，AC 平分∠BAD，则图中与∠AGE 相等的角有( D ) A．2 个 B．3 个 C．4 个 D．5 个 二、填空题(每小题 3 分，共 18 分) 11．把“k>0 时，正比例函数 y＝kx 的图象经过一、三象限”改写成“如果……，那 么……”的形式是__如果正比例函数 y＝kx 中，k>0，那么正比例函数的图象经过一、三象 限__． 12．(2014·广州)△ABC 中，已知∠A＝60°，∠B＝80°，则∠C 的外角的度数是__140° __． 13．如图，已知 AB∥CD，∠1＝∠B，∠2＝∠D，则∠BED＝__90°__． ,第 13 题图) ,第 14 题图) ,第 15 题图) ,第 16 题图) 14．如图，∠B＝30°，若 AB∥CD，CB 平分∠ACD，则∠ACD＝__60__度． 15．(2014·江西)如图，在△ABC 中，AB＝4，BC＝6，∠B＝60°，将△ABC 沿着射线 BC 的方向平移 2 个单位后，得到△A′B′C′，连接 A′C，则△A′B′C 的周长为__12__． 16．亲爱的同学们，在我们的生活中处处有数学的身影，请看图，折叠一张三角形纸片， 把三角形三个角拼在一起，就得到一个几何定理．请写出这个定理：__三角形内角和定理__． 三、解题题(共 72 分) 17．(6 分)判断下列命题是真命题还是假命题，请举出一个反例说明． (1)若 ab＝0，则 a＋b＝0； (2)如果 a 是无理数，b 是无理数，则 a＋b 是无理数． 解：(1)是假命题，若 a＝0，b＝4，ab＝0，但 a＋b≠0 (2)是假命题，若 a＝ 3，b ＝2－ 3，它们都是无理数，但 a＋b＝2 是有理数 18．(6 分)阅读理解并在括号内填注理由： 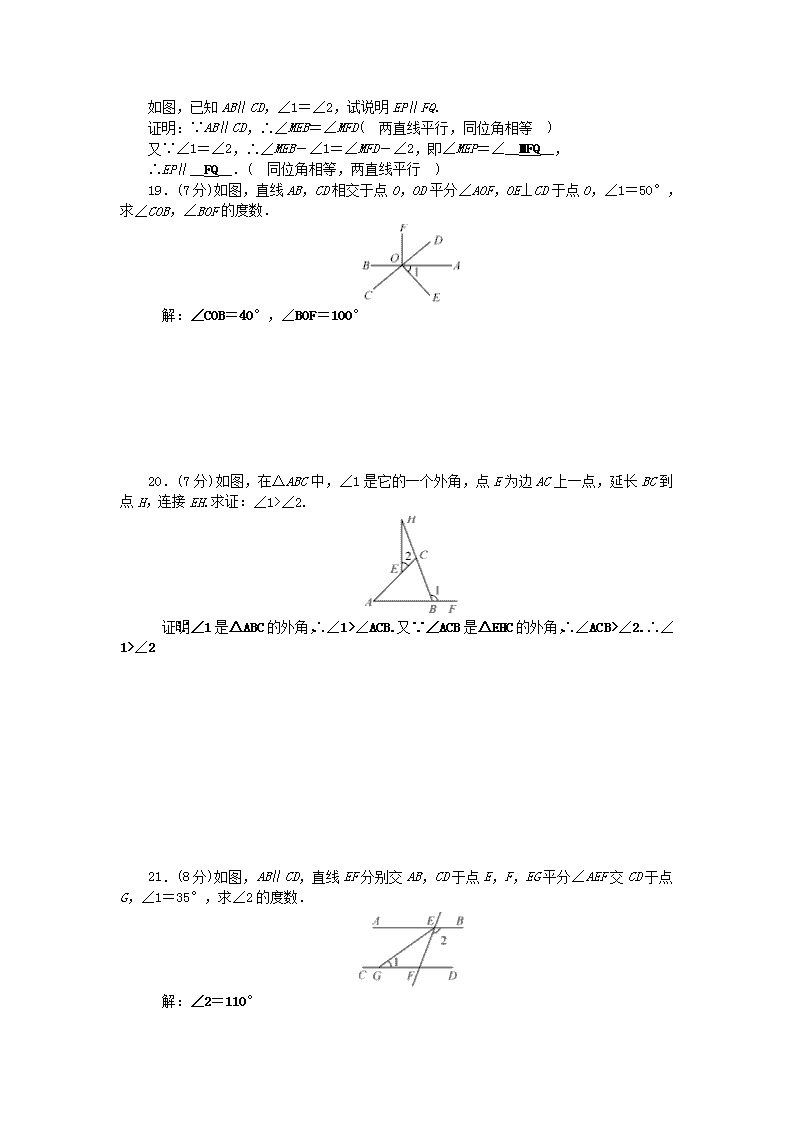如图，已知 AB∥CD，∠1＝∠2，试说明 EP∥FQ. 证明：∵AB∥CD，∴∠MEB＝∠MFD( 两直线平行，同位角相等 ) 又∵∠1＝∠2，∴∠MEB－∠1＝∠MFD－∠2，即∠MEP＝∠__MFQ__， ∴EP∥__FQ__．( 同位角相等，两直线平行 ) 19．(7 分)如图，直线 AB，CD 相交于点 O，OD 平分∠AOF，OE⊥CD 于点 O，∠1＝50°， 求∠COB，∠BOF 的度数． 解：∠COB＝40°，∠BOF＝100° 20．(7 分)如图，在△ABC 中，∠1 是它的一个外角，点 E 为边 AC 上一点，延长 BC 到 点 H，连接 EH.求证：∠1>∠2. 证明：∵∠1 是△ABC 的外角，∴∠1>∠ACB.又∵∠ACB 是△EHC 的外角，∴∠ACB> ∠2.∴∠1>∠2 21．(8 分)如图，AB∥CD，直线 EF 分别交 AB，CD 于点 E，F，EG 平分∠AEF 交 CD 于点 G，∠1＝35°，求∠2 的度数． 解：∠2＝110° 22．(8 分)如图，已知∠ABC＝∠ADC，BF，DE 是∠ABC，∠ADC 的角平分线，∠1＝∠2， 试说明：DC∥AB. 解：∵∠CDE＝1 2 ∠ADC，∠2＝1 2 ∠ABC，而∠ABC＝∠ADC，∴∠CDE＝∠2，又∠1＝ ∠2，∴∠CDE＝∠1，∴DC∥AB 23．(9 分)如图，已知 AD⊥BC 于 D，GE⊥BC 于 E，∠1＝∠G，说明：AD 平分∠BAC. 解：∵AD⊥BC，GE⊥BC，∴AD∥GE，∴∠1＝∠BAD，∠G＝∠CAD，而∠1＝∠G，∴ ∠BAD＝∠CAD，∴AD 平分∠BAC 24．(9 分)如图，已知∠1＋∠2＝180°，∠DEF＝∠A，∠BED＝60°，求∠ACB 的度数． 解：∵∠1＋∠2＝180°，∠1＋∠DFE＝180°，∴∠2＝∠DFE，∴AB∥EF，∴∠BDE ＝∠DEF，又∠DEF＝∠A，∴∠BDE＝∠A.∴DE∥AC，∴∠ACB＝∠DEB＝60° 25．(12 分)如图，BE，CD 相交于点 A，∠DEA，∠BCA 的平分线交于 F.探求∠F 与∠B， ∠D 有何等量关系？当∠B∶∠D∶∠F＝2∶4∶x 时，x 为多少？ 解：∠B＋∠D＝2∠F.∵∠DEA，∠BCA 的平分线交于 F.∴∠DEM＝∠FEN，∠FCM＝ ∠BCN.∵∠EMA 是△DME 的外角，∠ENC 是△BNC 的外角，∴∠EMA＝∠D＋∠DEM，∠ENC＝ ∠B＋∠BCN.又∵∠EMA 是△MFC 的外角．∠ENC 是△EFN 的外角，∴∠EMA＝∠F＋∠FCM， ∠ENC＝∠F＋∠FEN.∴∠F＋∠FCM＋∠F＋∠FEN＝∠D＋∠DEM＋∠B＋∠BCN.∴2∠F＝∠B ＋∠D.当∠B∶∠D∶∠F＝2∶4∶x 时，设∠B＝2k，∠D＝4k，∠F＝xk，由上面的结论可知： 2k＋4k＝2xk，解得 x＝3