苏科版八年级第一学期期中考试数学试题 4页

苏教版八年级数学上册期中考试测试卷 一、选择题（每小题 3 分，共 24 分） 1．下列图形中，轴对称图形是…………………………………………………………………（ ） A． B． C． D． 2．下列图形中有 4 条对称轴的图形是…………………………………………………………（ ） A． B． C． D． 3．下列各组图形中，一定是全等图形的是……………………………………………………（ ） A．两个周长相等的等腰三角形 B．两个面积相等的长方形 C．两个斜边相等的直角三角形 D．两个周长相等的圆 4．下列各数组中，不是勾股数的是………………………………………………………………（ ） A．5、12、13 B．12、18、22 C．7、24、25 D．9、12、15 5．如图，是一只停泊在平静水面上的小船，它的“倒影”应是图中的………………………（ ） A． B． C． D． 6．如图，∠AOB 的平分线上一点 P 到 OA 的距离为 5，Q 是 OB 上任意一点，则……………（ ） A．PQ≥5 B．PQ＞5 C．PQ≤5 D．PQ＜5 7．若等腰三角形有一个角等于 40°，则它的顶角等于…………………………………………（ ） A． 70° B． 40° C．100° D． 40°或 100° 8．如图，∠CAB=∠DBA，再添加一个条件，不一定能判定△ABC≌△BAD 的是…………（ ） A． AC=BD B．∠1=∠2 C．AD=BC D．∠C=∠D 二、填空题（每小题 2 分，共 20 分） 9． 等腰三角形的两边长分别为 3cm 和 6cm，则这个等腰三角形的周长为 cm． 10．等腰三角形底边上的高线长 5cm，则这个等腰三角形顶角的角平分线长 cm． 11．若直角三角形斜边长为 6cm，则斜边上的中线长为 cm． 12．某直角三角形三条边的平方和为 800，则这个直角三角形的斜边长为 ． 13．如图，△OAD≌△OBC，且∠O=72°，∠C=20°，则∠AEB= °． 14．如图为某楼梯的侧面，测得楼梯的斜长 AB 为 5 米，高 BC 为 3 米，计划在楼梯表面铺地毯，地毯的 长度至少需要 米． （第 6 题） （第 8 题） 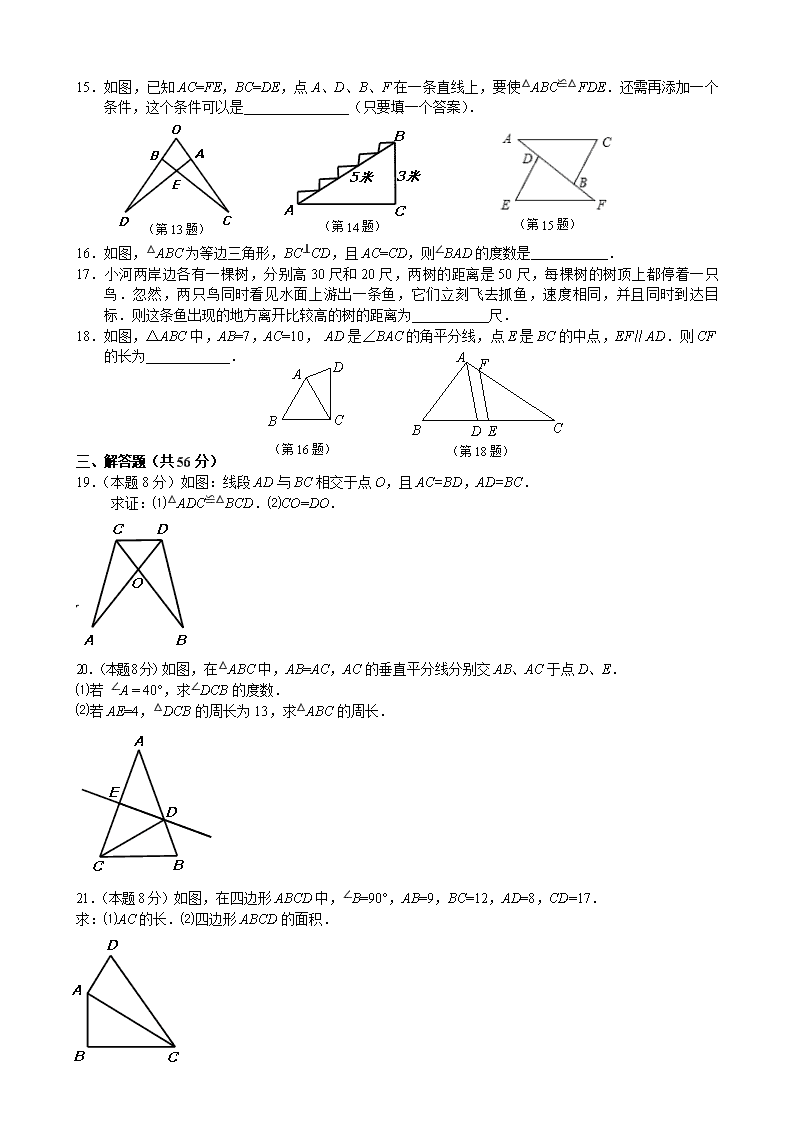15．如图，已知 AC=FE，BC=DE，点 A、D、B、F 在一条直线上，要使△ABC≌△FDE．还需再添加一个 条件，这个条件可以是 （只要填一个答案）． 16．如图，△ABC 为等边三角形，BC⊥CD，且 AC=CD，则∠BAD 的度数是 ． 17．小河两岸边各有一棵树，分别高 30 尺和 20 尺，两树的距离是 50 尺，每棵树的树顶上都停着一只鸟．忽 然，两只鸟同时看见水面上游出一条鱼，它们立刻飞去抓鱼，速度相同，并且同时到达目标．则这条 鱼出现的地方离开比较高的树的距离为___________尺． 18．如图，△ABC 中，AB=7，AC=10， AD 是∠BAC 的角平分线，点 E 是 BC 的中点，EF∥AD．则 CF 的长为 ． 三、解答题（共 56 分） 19．（本题 8 分）如图：线段 AD 与 BC 相交于点 O，且 AC=BD，AD=BC． 求证：⑴△ADC≌△BCD．⑵CO=DO． [来源:Zxxk. 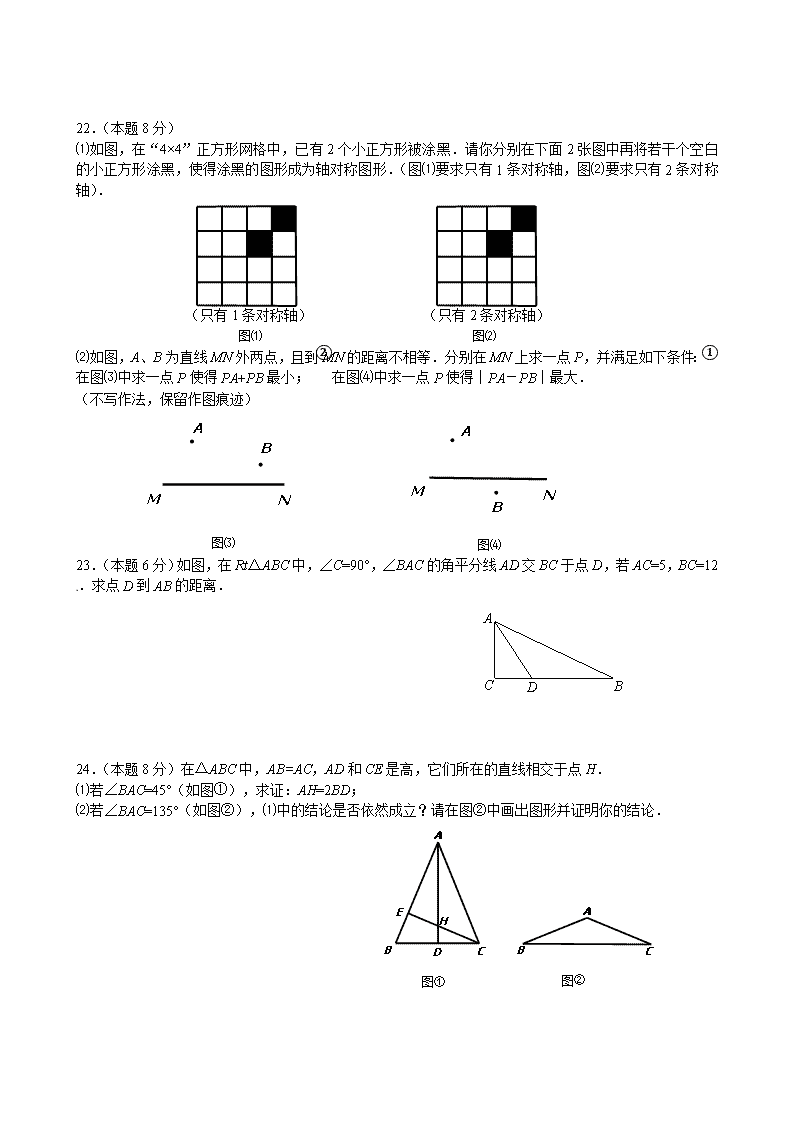20．（本题8分）如图，在△ABC 中，AB=AC，AC 的垂直平分线分别交 AB、AC 于点 D、E． ⑴若 ∠A = 40°，求∠DCB 的度数． ⑵若 AE=4，△DCB 的周长为 13，求△ABC 的周长． 21．（本题 8 分）如图，在四边形 ABCD 中，∠B=90°，AB=9，BC=12，AD=8，CD=17． 求：⑴AC 的长．⑵四边形 ABCD 的面积． （第 13 题） （第 14 题） （第 15 题） （第 18 题） A B CD E F （第 16 题） A B C D 22．（本题 8 分） ⑴如图，在“4×4”正方形网格中，已有 2 个小正方形被涂黑．请你分别在下面 2 张图中再将若干个．．．空白 的小正方形涂黑，使得涂黑的图形成为轴对称图形．（图⑴要求只有 1 条对称轴，图⑵要求只有 2 条对称 轴）． （只有 1 条对称轴） （只有 2 条对称轴） 图⑴ 图⑵ ⑵如图，A、B 为直线 MN 外两点，且到 MN 的距离不相等．分别在 MN 上求一点 P，并满足如下条件：① 在图⑶中求一点 P 使得 PA+PB 最小； ②在图⑷中求一点 P 使得｜PA－PB｜最大． （不写作法，保留作图痕迹） 23．（本题 6 分）如图，在 Rt△ABC 中，∠C=90°，∠BAC 的角平分线 AD 交 BC 于点 D，若 AC=5，BC=12．求 点 D 到 AB 的距离． 24．（本题 8 分）在△ABC 中，AB=AC，AD 和 CE 是高，它们所在的直线相交于点 H． ⑴若∠BAC=45°（如图①），求证：AH=2BD； ⑵若∠BAC=135°（如图②），⑴中的结论是否依然成立？请在图②中画出图形并证明你的结论． 图⑶ 图⑷ 图① 图② A BC D 25．（本题 10 分）如图，已知△ABC 中，AB=AC=6cm，BC=4cm，点 D 为 AB 的中点． ⑴如果点 P 在线段 BC 上以 1cm/s 的速度由点 B 向点 C 运动，同时，点 Q 在线段 CA 上由点 C 向点 A 运动． ①若点 Q 的运动速度与点 P 的运动速度相等，经过 1 秒后，△BPD 与△CPQ 是否全等，请说明理由． ②若点 Q 的运动速度与点 P 的运动速度不相等，当点 Q 的运动速度为____________cm/s 时，在某一 时刻也能够使△BPD 与△CPQ 全等． ⑵若点 Q 以②中的运动速度从点 C 出发，点 P 以原来的运动速度从点 B 同时出发，都逆时针沿△ABC 的 三边运动．求经过多少秒后，点 P 与点 Q 第一次相遇，并写出第一次相遇点在△ABC 的哪条边上？