(八年级下册数学)(期末压轴题汇编) 9页

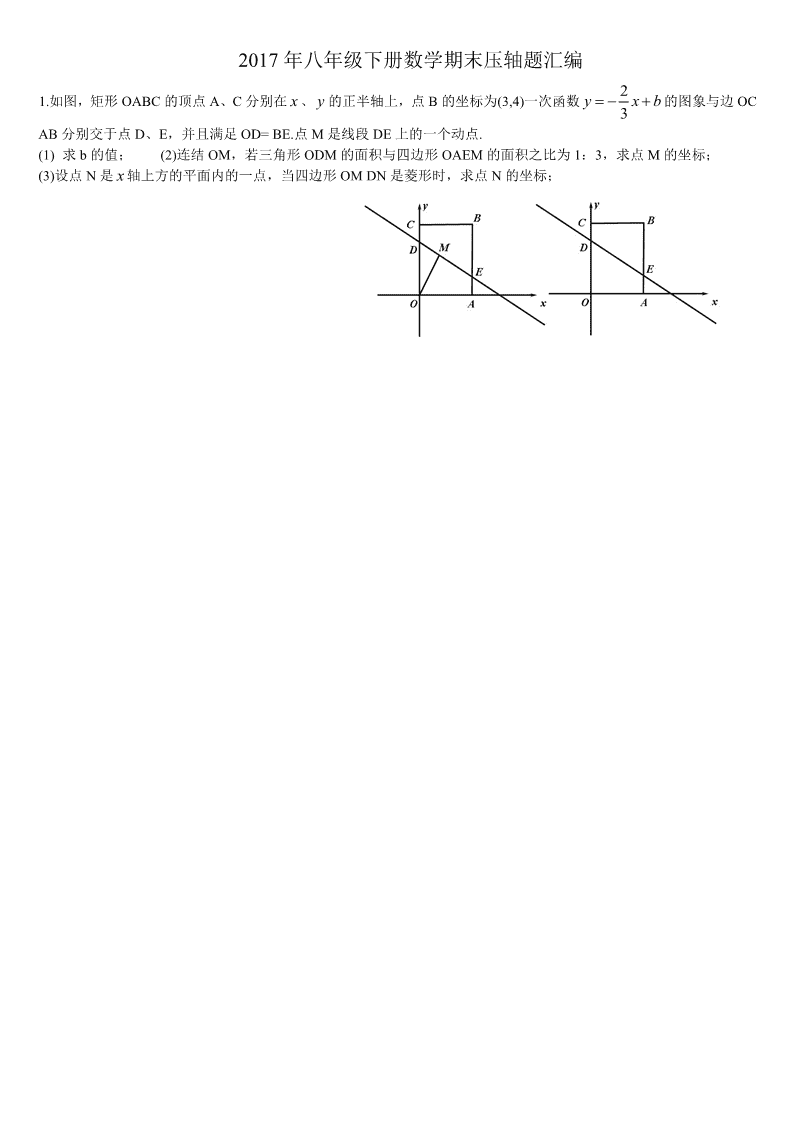
2017 年八年级下册数学期末压轴题汇编 1.如图，矩形 OABC 的顶点 A、C 分别在 x 、 y 的正半轴上，点 B 的坐标为(3,4)一次函数 2 3y x b   的图象与边 OC AB 分别交于点 D、E，并且满足 OD= BE.点 M 是线段 DE 上的一个动点. 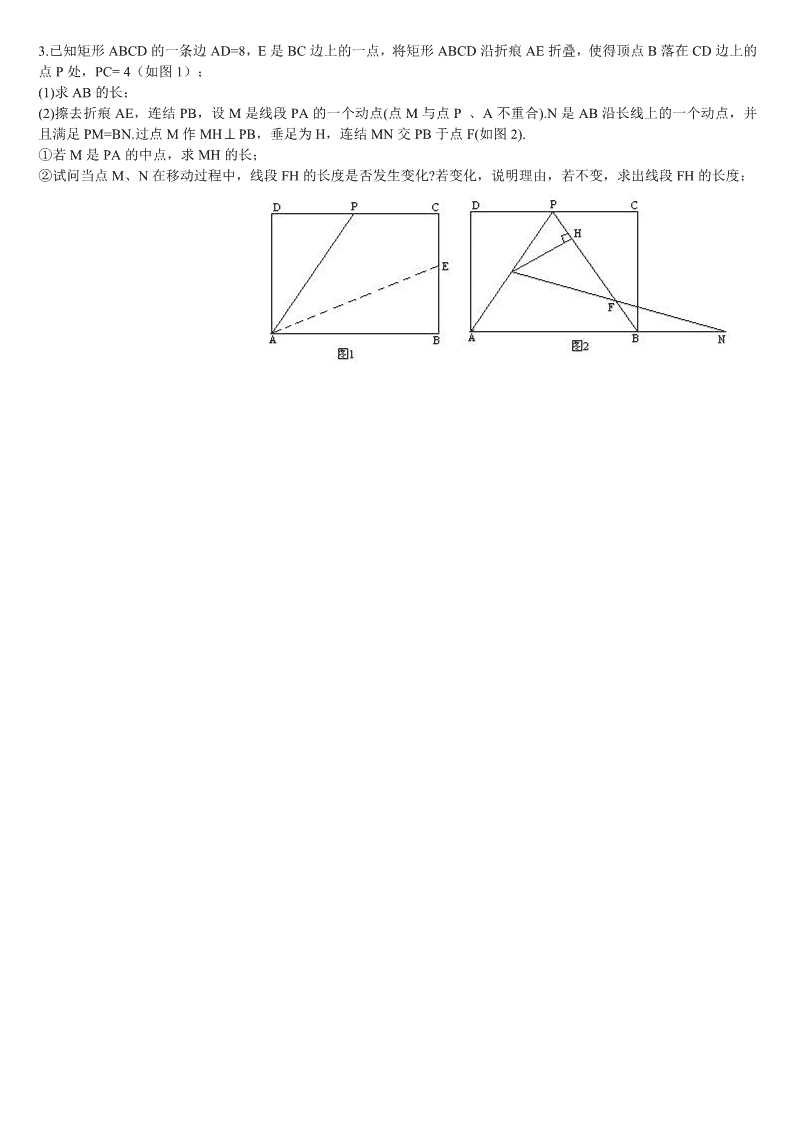(1) 求 b 的值； (2)连结 OM，若三角形 ODM 的面积与四边形 OAEM 的面积之比为 1：3，求点 M 的坐标； (3)设点 N 是 x 轴上方的平面内的一点，当四边形 OM DN 是菱形时，求点 N 的坐标； 2.如图，正方形 ABCD 中，P 为 BD 上一动点，过点 P 作 PQ⊥AP 交 CD 边于点 Q， ⑴求证：PA=PQ；⑵用等式表示 PB2、PD2、AQ2 之间的数量关系，并证明； ⑶点 P 从点 B 出发，沿 BD 方向移动，若移动的路径长为 2，则 AQ 的中点 M 移动的路径为---------------； （直接写出答案） 3.已知矩形 ABCD 的一条边 AD=8，E 是 BC 边上的一点，将矩形 ABCD 沿折痕 AE 折叠，使得顶点 B 落在 CD 边上的 点 P 处，PC= 4（如图 1）； (1)求 AB 的长； (2)擦去折痕 AE，连结 PB，设 M 是线段 PA 的一个动点(点 M 与点 P 、A 不重合).N 是 AB 沿长线上的一个动点，并 且满足 PM=BN.过点 M 作 MH  PB，垂足为 H，连结 MN 交 PB 于点 F(如图 2). ①若 M 是 PA 的中点，求 MH 的长； ②试问当点 M、N 在移动过程中，线段 FH 的长度是否发生变化?若变化，说明理由，若不变，求出线段 FH 的长度； 4.如图，在四边形 ABCD 中，AD∥BC，∠B=90°，AD=6，BC=9，动点 P 从 D 点出发沿 DA 以每秒 1 个单位的速度 向 A 点运动，动点 Q 从 B 点出发沿 BC 以每秒 3 个单位的速度向 C 点运动．两点同时出发，当 Q 点到达 C 点时，点 P 随之停止运动．设点 P 运动的时间为 t 秒； （1）求 t 的取值范围； （2）求 t 为何值时，PQ 与 CD 相等？ 5.已知：四边形 ABCD 是正方形，E 是 AB 边上一点，连接 DE，过点 D 作 DF⊥DE 交 BC 的延长线于点 F，连接 EF． （1）如图 1，求证：DE=DF； （2）若点 D 关于直线 EF 的对称点为 H，连接 CH，过点 H 作 PH⊥CH 交直线 AB 于点 P； ①在图 2 中依题意补全图形； ②求证：E 为 AP 的中点； （3）如图 3，连接 AC 交 EF 于点 M，求 2AM AB AE 的值； 6.如图，在平面直角坐标系 xOy 中，直线 l 与 x 轴交于点 A（ 4 ，0 ），与 y 轴的正半轴交于点 B．点 C 在直线 1  y x 上，且 CA⊥x 轴于点 A； （1）求点 C 的坐标； （2）若点 D 是 OA 的中点，点 E 是 y 轴上一个动点，当 EC+ED 最小时，求此时点 E 的坐标； （3）若点 A 恰好在 BC 的垂直平分线上，点 F 在 x 轴上，且△ABF 是以 AB 为腰的等腰三角形，请直接写出所有满足 条件的点 F 的坐标； 7.把一个含 45°角的直角三角板 BEF 和一个正方形 ABCD 摆放在一起，使三角板的直角顶点和正方形的顶点 B 重合， 联结 DF，点 M，N 分别为 DF，EF 的中点，联结 MA，MN． （1）如图 1，点 E，F 分别在正方形的边 CB，AB 上，请判断 MA，MN 的数量关系和位置关系，直接写出结论； （2）如图 2，点 E，F 分别在正方形的边 CB，AB 的延长线上，其他条件不变，那么你在（1）中得到的两个结论还 成立吗？若成立，请加以证明；若不成立，请说明理由； 图 1 图 2 8 有一项工作，由甲、乙合作完成，工作一段时间后，甲改进了技术，提高了工作效率．设甲的工作量为 y 甲（件）， 乙的工作量为 y 乙（件），甲、乙合作完成的工作量为 y（件），工作时间为 x（时），y 与 x 之间的部分函数图象如图 ①所示，y 乙与 x 之间的部分函数图象如图②所示； （1）分别求出甲 2 小时、6 小时的工作量； （2）当 0≤x≤6 时，在图②中画出 y 甲与 x 的函数图象，并求出 y 甲与 x 之间的函数关系式； （3）求工作几小时，甲、乙完成的工作量相等； （4）若 6 小时后，甲保持第 6 小时的工作效率，乙改进了技术，提高了工作效率，当 x=8 时，甲、乙之间的工作量相 差 30 件，求乙提高工作效率后平均每小时做多少件； 9.如图，在平行四边形 ABCD 中，∠BAD 的平分线交直线 BC 于 E，交直线 DC 于点 F，以 CF 为邻边作平行四边形 ECFG； （1）如图 1，证明平行四边形 ECFG 为菱形； （2）如图 2，若∠ABC=90°，M 是 EF 的中点，求∠BDM 的度数； （3）如图 3，若∠ABC=120°，请直接写出∠BDG 的度数；