数学人教版八年级上册 期末试卷（2） 22页

第 1页（共 22页） 期末试卷（2） 一、选择题（本题有 10 小题，每小题 4 分，共 40 分，请选出各题中一个符合 题意的正确选项，不选、多选、错选，均不给分） 1．（4 分）将下列四种长度的三根木棒首尾顺次连接，能组成三角形的是（ ） A．2，5，8 B．3，4，5 C．2，2，4 D．1，2，3 2．（4 分）下列图形是对圆的面积进行四等分的几种作图，则它们是轴对称图形 的个数为（ ） A．1 B．2 C．3 D．4 3．（4 分）下列运算中，正确的是（ ） A．（a2）3=a5 B．a2•a4=a6 C．3a2÷2a=a D．（2a）2=2a2 4．（4 分）若分式 的值是零，则 x 的值是（ ） A．x=﹣2 B．x=±3 C．2 D．x=3 5．（4 分）长方形的面积为 x2﹣2xy+x，其中一边长是 x，则另一边长是（ ） A．x﹣2y B．x+2yC．x﹣2y﹣1 D．x﹣2y+1 6．（4 分）如图，E，B，F，C 四点在一条直线上，EB=CF，∠A=∠D，再添一个 条件仍不能证明△ABC≌△DEF 的是（ ） A．AB=DE B．DF∥AC C．∠E=∠ABC D．AB∥DE 7．（4 分）如图所示，∠AOP=∠BOP=15°，PC∥OA，PD⊥OA，若 PC=4，则 PD 等于（ ） A．4 B．3 C．2 D．1 第 2页（共 22页） 8．（4 分）如图（1），是一个长为 2a 宽为 2b（a＞b）的矩形，用剪刀沿矩形的 两条对角轴剪开，把它分成四个全等的小矩形，然后按图（2）拼成一个新的正 方形，则中间空白部分的面积是（ ） A．ab B．（a+b）2 C．（a﹣b）2 D．a2﹣b2 9．（4 分）“五水共治”工程中，要挖掘一段 a 千米的排污管沟，如果由 10 个工人 挖掘，要用 m 天完成；如果由一台挖掘机工作，要比 10 个工人挖掘提前 3 天完 成，一台挖掘机的工作效率是一个工人工作效率的（ ） A． B． C． D． 10．（4 分）在平面直角坐标系 xOy 中，对于点 P（x，y），我们把点 P1（﹣y+1， x+1）叫做点 P 的伴随点，已知点 A1 的伴随点为 A2，点 A2 的伴随点为 A3，点 A3 的伴随点为 A4，…，这样依次得到点 A1，A2，A3，…，An，若点 A1 的坐标为（3， 1），则点 A2015 的坐标为（ ） A．（0，4） B．（﹣3，1） C．（0，﹣2） D．（3，1） 二、填空题（本题有 6 小题，每小题 5 分，共 30 分 11．（5 分）点 A（﹣3，2）关于 x 轴的对称点 A′的坐标为 ． 12．（5 分）因式分解：x2﹣4y2= ． 13．（5 分）等腰三角形一边等于 4，另一边等于 2，则周长是 ． 14．（5 分）若 a﹣b=5，ab=3，则 a2+b2= ． 15．（5 分）当三角形中一个内角α是另一个内角β的两倍时，我们称此三角形为“特 征三角形”，其中α称为“特征角”．如果一个直角三角形为“特征三角形”，那么它 的“特征角”等于 度． 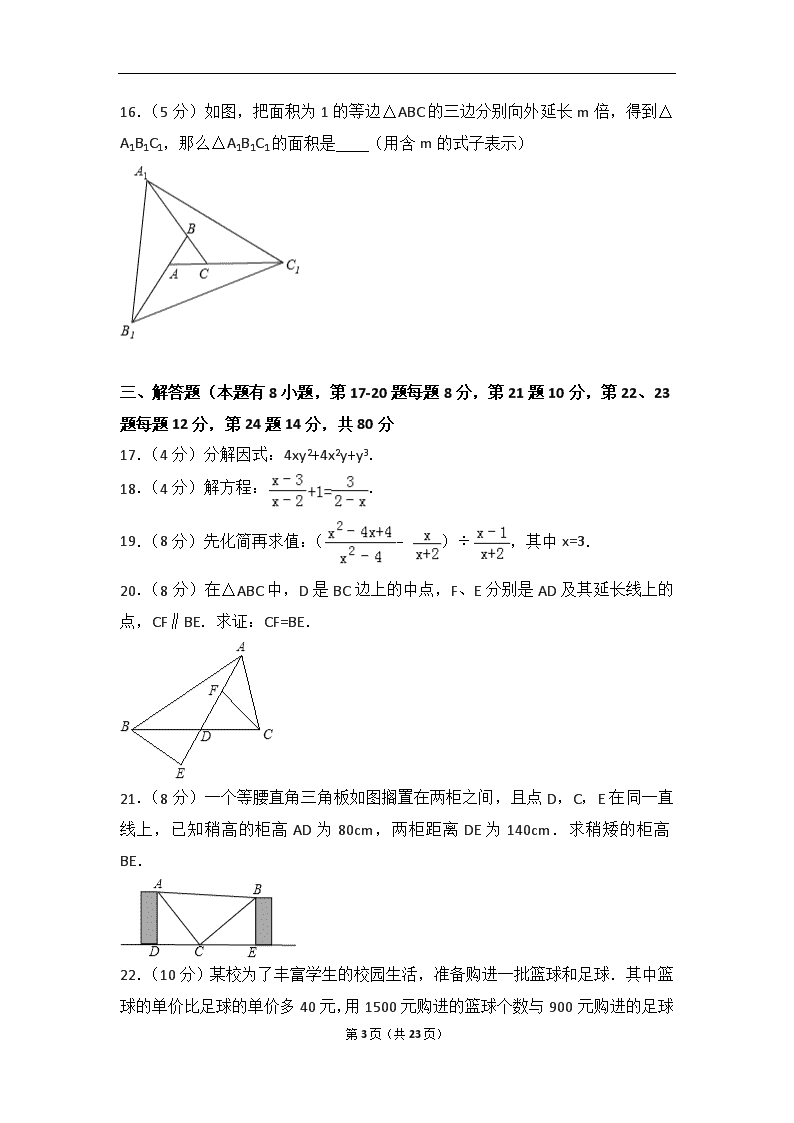16．（5 分）如图，把面积为 1 的等边△ABC 的三边分别向外延长 m 倍，得到△ A1B1C1，那么△A1B1C1 的面积是 （用含 m 的式子表示） 第 3页（共 22页） 三、解答题（本题有 8 小题，第 17-20 题每题 8 分，第 21 题 10 分，第 22、23 题每题 12 分，第 24 题 14 分，共 80 分 17．（4 分）分解因式：4xy2+4x2y+y3． 18．（4 分）解方程： ． 19．（8 分）先化简再求值：（ ﹣ ）÷ ，其中 x=3． 20．（8 分）在△ABC 中，D 是 BC 边上的中点，F、E 分别是 AD 及其延长线上的 点，CF∥BE．求证：CF=BE． 21．（8 分）一个等腰直角三角板如图搁置在两柜之间，且点 D，C，E 在同一直 线上，已知稍高的柜高 AD 为 80cm，两柜距离 DE 为 140cm．求稍矮的柜高 BE． 22．（10 分）某校为了丰富学生的校园生活，准备购进一批篮球和足球．其中篮 球的单价比足球的单价多 40 元，用 1500 元购进的篮球个数与 900 元购进的足球 个数相等． （1）篮球和足球的单价各是多少元？ （2）该校打算用 800 元购买篮球和足球，恰好用完 800 元，问有哪几种购买方 第 4页（共 22页） 案？ 23．（12 分）探究题： （1） 都相等， 都相等的多边形叫做正多边形； （2）如图，格点长方形 MNPQ 的各点分布在边长均为 1 的等边三角形组成的网 格上，请在格点长方形 MNPQ 内画出一个面积最大的格点正六边形 ABCDEF，并 简要说明它是正六边形的理由； （3）正六边形有 条对角线，它的外角和为 度． 24．（12 分）阅读理解：（请仔细阅读，认真思考，灵活应用） 【例】已知实数 x 满足 x+ =4，求分式 的值． 解：观察所求式子的特征，因为 x≠0，我们可以先求出 的倒数的值， 因为 =x+3+ =x+ +3=4+3=7 所以 = 【活学活用】 （1）已知实数 a 满足 a+ =﹣5，求分式 的值； （2）已知实数 x 满足 x+ =9，求分式 的值． 25．（14 分）有公共顶点 A 的△ABD，△ACE 都是的等边三角形． （1）如图 1，将△ACE 绕顶点 A 旋转，当 E，C，B 共线时，求∠BCD 的度数； （2）如图 2，将△ACE 绕顶点 A 旋转，当∠ACD=90°时，延长 EC 角 BD 于 F， ①求证：∠DCF=∠BEF； ②写出线段 BF 与 DF 的数量关系，并说明理由． 第 5页（共 22页） 第 6页（共 22页） 参考答案与试题解析 一、选择题（本题有 10 小题，每小题 4 分，共 40 分，请选出各题中一个符合 题意的正确选项，不选、多选、错选，均不给分） 1．（4 分）将下列四种长度的三根木棒首尾顺次连接，能组成三角形的是（ ） A．2，5，8 B．3，4，5 C．2，2，4 D．1，2，3 【考点】三角形三边关系． 【分析】根据三角形三边关系定理：三角形两边之和大于第三边进行分析即可． 【解答】解：A、2+5＜8，不能组成三角形，故此选项错误； B、3+4＞5，能组成三角形，故此选项正确； C、2+2=4，不能组成三角形，故此选项错误； D、1+2=3，不能组成三角形，故此选项错误； 故选：B． 【点评】此题主要考查了三角形的三边关系定理，在运用三角形三边关系判定三 条线段能否构成三角形时并不一定要列出三个不等式，只要两条较短的线段长度 之和大于第三条线段的长度即可判定这三条线段能构成一个三角形． 2．（4 分）下列图形是对圆的面积进行四等分的几种作图，则它们是轴对称图形 的个数为（ ） A．1 B．2 C．3 D．4 【考点】轴对称图形． 【分析】根据轴对称图形的概念求解即可． 【解答】解：第一个图形是轴对称图形； 第二个图形是轴对称图形； 第三个图形不是轴对称图形； 第四个图形是轴对称图形； 第 7页（共 22页） 所以一共有三个轴对称图形． 故选 C． 【点评】本题考查了轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形 两部分折叠后可重合． 3．（4 分）下列运算中，正确的是（ ） A．（a2）3=a5 B．a2•a4=a6 C．3a2÷2a=a D．（2a）2=2a2 【考点】整式的除法；同底数幂的乘法；幂的乘方与积的乘方． 【专题】计算题；整式． 【分析】A、原式利用幂的乘方运算法则计算得到结果，即可作出判断； B、原式利用同底数幂的乘法法则计算得到结果，即可作出判断； C、原式利用单项式除以单项式法则计算得到结果，即可作出判断； D、原式利用积的乘方运算法则计算得到结果，即可作出判断． 【解答】解：A、原式=a6，错误； B、原式=a6，正确； C、原式= a，错误； D、原式=4a2，错误， 故选 B 【点评】此题考查了整式的除法，同底数幂的乘法，以及幂的乘方与积的乘方， 熟练掌握运算法则是解本题的关键． 4．（4 分）若分式 的值是零，则 x 的值是（ ） A．x=﹣2 B．x=±3 C．2 D．x=3 【考点】分式的值为零的条件． 【分析】直接利用分式的值为 0，则分子为 0，进而得出答案． 【解答】解：∵分式 的值是零， ∴x+2=0， 第 8页（共 22页） 解得：x=﹣2． 故选：A． 【点评】此题主要考查了分式的值为零的条件，正确把握定义是解题关键． 5．（4 分）长方形的面积为 x2﹣2xy+x，其中一边长是 x，则另一边长是（ ） A．x﹣2y B．x+2yC．x﹣2y﹣1 D．x﹣2y+1 【考点】整式的除法． 【专题】计算题；整式． 【分析】根据面积除以一边长得到另一边长即可． 【解答】解：根据题意得：（x2﹣2xy+x）÷x=x﹣2y+1， 故选 D 【点评】此题考查了整式的除法，熟练掌握除法法则是解本题的关键． 6．（4 分）如图，E，B，F，C 四点在一条直线上，EB=CF，∠A=∠D，再添一个 条件仍不能证明△ABC≌△DEF 的是（ ） A．AB=DE B．DF∥AC C．∠E=∠ABC D．AB∥DE 【考点】全等三角形的判定． 【分析】由 EB=CF，可得出 EF=BC，又有∠A=∠D，本题具备了一组边、一组角 对应相等，为了再添一个条件仍不能证明△ABC≌△DEF，那么添加的条件与原 来的条件可形成 SSA，就不能证明△ABC≌△DEF 了． 【解答】解：A、添加 DE=AB 与原条件满足 SSA，不能证明△ABC≌△DEF，故 A 选项正确． B、添加 DF∥AC，可得∠DFE=∠ACB，根据 AAS 能证明△ABC≌△DEF，故 B 选项 错误． C、添加∠E=∠ABC，根据 AAS 能证明△ABC≌△DEF，故 C 选项错误． D、添加 AB∥DE，可得∠E=∠ABC，根据 AAS 能证明△ABC≌△DEF，故 D 选项 第 9页（共 22页） 错误． 故选：A． 【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有： SSS、SAS、ASA、AAS、HL． 注意：AAA、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边 的参与，若有两边一角对应相等时，角必须是两边的夹角． 7．（4 分）如图所示，∠AOP=∠BOP=15°，PC∥OA，PD⊥OA，若 PC=4，则 PD 等于（ ） A．4 B．3 C．2 D．1 【考点】菱形的判定与性质；含 30 度角的直角三角形． 【专题】几何图形问题． 【分析】过点 P 做 PM∥CO 交 AO 于 M，可得∠CPO=∠POD，再结合题目推出四 边形 COMP 为菱形，即可得 PM=4，又由 CO∥PM 可得∠PMD=30°，由直角三角 形性质即可得 PD． 【解答】解：如图：过点 P 做 PM∥CO 交 AO 于 M，PM∥CO ∴∠CPO=∠POD，∠AOP=∠BOP=15°，PC∥OA ∴四边形 COMP 为菱形，PM=4 PM∥CO ⇒ ∠PMD=∠AOP+∠BOP=30°， 又∵PD⊥OA ∴PD= PC=2． 令解：作 CN⊥OA． ∴CN= OC=2， 又∵∠CNO=∠PDO， ∴CN∥PD， 第 10页（共 22页） ∵PC∥OD， ∴四边形 CNDP 是长方形， ∴PD=CN=2 故选：C． 【点评】本题运用了平行线和直角三角形的性质，并且需通过辅助线求解，难度 中等偏上． 8．（4 分）如图（1），是一个长为 2a 宽为 2b（a＞b）的矩形，用剪刀沿矩形的 两条对角轴剪开，把它分成四个全等的小矩形，然后按图（2）拼成一个新的正 方形，则中间空白部分的面积是（ ） A．ab B．（a+b）2 C．（a﹣b）2 D．a2﹣b2 【考点】完全平方公式的几何背景． 【分析】先求出正方形的边长，继而得出面积，然后根据空白部分的面积=正方 形的面积﹣矩形的面积即可得出答案． 【解答】解：由题意可得，正方形的边长为（a+b）， 故正方形的面积为（a+b）2， 又∵原矩形的面积为 4ab， ∴中间空的部分的面积=（a+b）2﹣4ab=（a﹣b）2． 故选 C． 【点评】此题考查了完全平方公式的几何背景，求出正方形的边长是解答本题的 关键，难度一般． 第 11页（共 22页） 9．（4 分） “五水共治”工程中，要挖掘一段 a 千米的排污管沟，如果由 10 个工 人挖掘，要用 m 天完成；如果由一台挖掘机工作，要比 10 个工人挖掘提前 3 天 完成，一台挖掘机的工作效率是一个工人工作效率的（ ） A． B． C． D． 【考点】列代数式（分式）． 【分析】此题可利用工作总量作为相等关系，借助方程解题． 【解答】解：设一台插秧机的工作效率为 x，一个人工作效率为 y． 则 10my=（m﹣3）x． 所以 = ， 故选：D． 【点评】本题主要考查了列代数式的知识，列代数式的关键是正确理解文字语言 中的关键词，找到其中的数量关系，工程问题要有“工作效率”，“工作时间”，“工 作总量”三个要素，数量关系为：工作效率×工作时间=工作总量． 10．（4 分）在平面直角坐标系 xOy 中，对于点 P（x，y），我们把点 P1（﹣y+1， x+1）叫做点 P 的伴随点，已知点 A1 的伴随点为 A2，点 A2 的伴随点为 A3，点 A3 的伴随点为 A4，…，这样依次得到点 A1，A2，A3，…，An，若点 A1 的坐标为（3， 1），则点 A2015 的坐标为（ ） A．（0，4） B．（﹣3，1） C．（0，﹣2） D．（3，1） 【考点】规律型：点的坐标． 【分析】根据伴随点的定义，罗列出部分点 A 的坐标，根据点 A 的变化找出规 律“A4n+1（3，1），A4n+2（0，4），A4n+3（﹣3，1），A4n+4（0，﹣2）（n 为自然数）”， 根据此规律即可解决问题． 【解答】解：观察，发现规律：A1（3，1），A2（0，4），A3（﹣3，1），A4（0， ﹣2），A5（3，1），…， ∴A4n+1（3，1），A4n+2（0，4），A4n+3（﹣3，1），A4n+4（0，﹣2）（n 为自然数）． ∵2015=4×503+3， ∴点 A2015 的坐标为（﹣3，1）． 故选 B． 第 12页（共 22页） 【点评】本题考查了规律型中的点的坐标，解题的关键是发现规律“A4n+1（3，1）， A4n+2（0，4），A4n+3（﹣3，1），A4n+4（0，﹣2）（n 为自然数）”．本题属于基础 题，难度不大，解决该题型题目时，罗列出部分点的坐标，根据点的坐标的变化 发现规律是关键． 二、填空题（本题有 6 小题，每小题 5 分，共 30 分 11．（5 分）点 A（﹣3，2）关于 x 轴的对称点 A′的坐标为 （﹣3，﹣2） ． 【考点】关于 x 轴、y 轴对称的点的坐标． 【分析】根据“关于 x 轴对称的点，横坐标相同，纵坐标互为相反数”解答． 【解答】解：点 A（﹣3，2）关于 x 轴对称的点的坐标为（﹣3，﹣2）． 故答案为：（﹣3，﹣2）． 【点评】本题考查了关于 x 轴、y 轴对称的点的坐标，解决本题的关键是掌握好 对称点的坐标规律： （1）关于 x 轴对称的点，横坐标相同，纵坐标互为相反数； （2）关于 y 轴对称的点，纵坐标相同，横坐标互为相反数； （3）关于原点对称的点，横坐标与纵坐标都互为相反数． 12．（5 分）因式分解：x2﹣4y2= （x+2y）（x﹣2y） ． 【考点】因式分解-运用公式法． 【分析】直接运用平方差公式进行因式分解． 【解答】解：x2﹣4y2=（x+2y）（x﹣2y）． 【点评】本题考查了平方差公式分解因式，熟记公式结构是解题的关键．平方差 公式：a2﹣b2=（a+b）（a﹣b）． 13．（5 分）等腰三角形一边等于 4，另一边等于 2，则周长是 10 ． 【考点】等腰三角形的性质；三角形三边关系． 【分析】因为等腰三角形的两边分别为 4 和 2，但没有明确哪是底边，哪是腰， 所以有两种情况，需要分类讨论． 【解答】解：当 4 为底时，其它两边都为 2，2、2、4 不可以构成三角形； 第 13页（共 22页） 当 4 为腰时，其它两边为 4 和 2，4、4、2 可以构成三角形，周长为 10， 故答案为：10． 【点评】本题考查了等腰三角形的性质及三角形三边关系；对于底和腰不等的等 腰三角形，若条件中没有明确哪边是底哪边是腰时，应在符合三角形三边关系的 前提下分类讨论． 14．（5 分）若 a﹣b=5，ab=3，则 a2+b2= 31 ． 【考点】完全平方公式． 【专题】计算题；整式． 【分析】把 a﹣b=5 两边平方，利用完全平方公式化简，将 ab=3 代入即可求出所 求式子的值． 【解答】解：把 a﹣b=5 两边平方得：（a﹣b）2=a2+b2﹣2ab=25， 将 ab=3 代入得：a2+b2=31， 故答案为：31 【点评】此题考查了完全平方公式，熟练掌握完全平方公式是解本题的关键． 15．（5 分）当三角形中一个内角α是另一个内角β的两倍时，我们称此三角形为“特 征三角形”，其中α称为“特征角”．如果一个直角三角形为“特征三角形”，那么它 的“特征角”等于 90 或 60 度． 【考点】三角形内角和定理． 【分析】根据“特征角”的定义，结合直角三角形的性质即可得出结论． 【解答】解：①“特征角”α为 90°； ②“特征角”与“另一个内角”都不是直角时，设“特征角是 2x”， 由题意得，x+2x=90°， 解得：x=30°， 所以，“特征角”是 60°， 综上所述，这个“特征角”的度数为 90°或 60°． 故答案为：90 或 60． 【点评】本题考查的是三角形内角和定理，熟知三角形内角和是 180°是解答此题 第 14页（共 22页） 的关键． 16．（5 分）如图，把面积为 1 的等边△ABC 的三边分别向外延长 m 倍，得到△ A1B1C1，那么△A1B1C1 的面积是 3m2+3m+1 （用含 m 的式子表示） 【考点】等边三角形的性质． 【分析】连接 AB1，BC1，CA1，根据等底等高的三角形的面积相等求出△ABB1， △A1AB1 的面积，从而求出△A1BB1 的面积，同理可求△B1CC1 的面积，△A1AC1 的面积，然后相加即可得解． 【解答】解：如图，连接 AA1，B1C2，BC1，如图所示： ∵把面积为 1 的等边△ABC 的三边分别向外延长 m 倍， ∴△A1 AB 的面积=△BC2C1 的面积=△AB1C2 的面积=m×1=m， 同理：△A1B1 A 的面积=△B1 C1 C2 的面积=△A1 BC1 的面积=m×m=m2， ∴△A1B1C1 的面积=3m2+3m+1； 故答案为：3m2+3m+1． 【点评】本题考查了三角形的面积，主要利用了等底等高的三角形的面积相等， 作辅助线把三角形进行分割是解题的关键． 三、解答题（本题有 8 小题，第 17-20 题每题 8 分，第 21 题 10 分，第 22、23 题每题 12 分，第 24 题 14 分，共 80 分 17．（4 分）分解因式：4xy2+4x2y+y3． 第 15页（共 22页） 【考点】提公因式法与公式法的综合运用． 【分析】首先提取公因式 y，进而利用完全平方公式分解因式得出答案． 【解答】解：4xy2+4x2y+y3 =y（4xy+4x2+y2） =y（y+2x）2． 【点评】此题主要考查了提取公因式法以及公式法分解因式，正确应用公式是解 题关键． 18．（4 分）解方程： ． 【考点】解分式方程． 【专题】计算题． 【分析】观察可得 2﹣x=﹣（x﹣2），所以可确定方程最简公分母为：（x﹣2），然 后去分母将分式方程化成整式方程求解．注意检验． 【解答】解：方程两边同乘以（x﹣2）， 得：x﹣3+（x﹣2）=﹣3， 解得 x=1， 检验：x=1 时，x﹣2≠0， ∴x=1 是原分式方程的解． 【点评】（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程 求解． （2）解分式方程一定注意要验根． （3）去分母时有常数项的不要漏乘常数项． 19．（8 分）先化简再求值：（ ﹣ ）÷ ，其中 x=3． 【考点】分式的化简求值． 【分析】先约分化简，再计算括号，最后代入化简即可． 【解答】解：原式=[ ﹣ }× 第 16页（共 22页） =（ ）× = × =﹣ ， 当 x=3 时，原式=﹣1 【点评】本题考查分式的混合运算、乘法公式等知识，解题的关键是灵活掌握分 式的混合运算法则，注意简便运算，属于中考常考题型． 20．（8 分）在△ABC 中，D 是 BC 边上的中点，F、E 分别是 AD 及其延长线上的 点，CF∥BE．求证：CF=BE． 【考点】全等三角形的判定与性质． 【专题】证明题． 【分析】利用 CF∥BE 和 D 是 BC 边的中点可以得到全等条件证明△BDE≌△CDF， 从而得出结论． 【解答】证明：∵D 是 BC 边上的中点， ∴BD=CD， 又∵CF∥BE， ∴∠E=∠CFD，∠DBE=∠FCD ∴△BDE≌△CFD， ∴CF=BE． 【点评】本题主要考查了全等三角形的判定与性质，难度适中． 21．（8 分）一个等腰直角三角板如图搁置在两柜之间，且点 D，C，E 在同一直 线上，已知稍高的柜高 AD 为 80cm，两柜距离 DE 为 140cm．求稍矮的柜高 BE． 第 17页（共 22页） 【考点】全等三角形的应用． 【分析】首先证明△ADC≌△CEB，根据全等三角形的性质可得 AD=CE，DC=BE， 进而可得 CE 的长，然后可得 DC 的长度，从而求出 BE 长． 【解答】解：由题意得：∠ADC=∠ACB=∠BEC=90°，AC=BC， ∵∠ACB=90°， ∴∠ACD+∠BCE=90°， ∵∠BEC=90°， ∴∠BCE+∠CBE=90°， ∴∠ACD=∠CBE， 在△ADC 和△CEB 中， ， ∴△ADC≌△CEB（AAS）， ∴AD=CE，DC=BE， ∵AD=80cm， ∴CE=80cm， ∵DE=140cm， ∴DC=60cm， ∴BE=60cm． 【点评】此题主要考查了全等三角形的应用，关键是掌握全等三角形的判定定理： SSS、SAS、ASA、AAS、HL． 22．（10 分）某校为了丰富学生的校园生活，准备购进一批篮球和足球．其中篮 球的单价比足球的单价多 40 元，用 1500 元购进的篮球个数与 900 元购进的足球 个数相等． （1）篮球和足球的单价各是多少元？ （2）该校打算用 800 元购买篮球和足球，恰好用完 800 元，问有哪几种购买方 案？ 第 18页（共 22页） 【考点】分式方程的应用；二元一次方程的应用． 【分析】（1）设足球单价为 x 元，则篮球单价为（x+40）元，根据题意可得等量 关系：1500 元购进的篮球个数=900 元购进的足球个数，由等量关系可得方程， 再求解即可； （2）设恰好用完 800 元，可购买篮球 m 个和购买足球 n 个，根据题意可得篮球 的单价×篮球的个数 m+足球的单价×足球的个数 n=800，再求出整数解即可得 出答案． 【解答】解：设足球单价为 x 元，则篮球单价为（x+40）元，由题意得： = ， 解得：x=60， 经检验：x=60 是原分式方程的解， 则 x+40=100， 答：篮球和足球的单价各是 100 元，60 元； （2）设恰好用完 800 元，可购买篮球 m 个和购买足球 n 个， 由题意得：100m+60n=800， 整理得：m=8﹣ n， ∵m、n 都是正整数， ∴①n=5 时，m=5，②n=10 时，m=2； ∴有两种方案： ①购买篮球 5 个，购买足球 5 个； ②购买篮球 2 个，购买足球 10 个． 【点评】此题主要考查了分式方程和二元一次方程的应用，关键是正确理解题意， 找出题目中的等量关系，列出方程． 23．（12 分）探究题： （1） 各个角 都相等， 各条边 都相等的多边形叫做正多边形； （2）如图，格点长方形 MNPQ 的各点分布在边长均为 1 的等边三角形组成的网 格上，请在格点长方形 MNPQ 内画出一个面积最大的格点正六边形 ABCDEF，并 简要说明它是正六边形的理由； 第 19页（共 22页） （3）正六边形有 9 条对角线，它的外角和为 360 度． 【考点】正多边形和圆． 【分析】（1）直接用正多边形的定义得出结论即可； （2）用网格线的特征和正六边形的性质，画出图形即可； （3）根据多边形的对角线条数的确定方法和多边形的外角和定理即可． 【解答】解：（1）由正多边形的定义：各个角都相等，各条边都相等的多边形叫 做正多边形； 故答案为：各个角；各条边； （2）如图， ∵AB=2，BC=2，CD=2，DE=2，EF=2，FA=2， ∴AB=BC=CD=DE=EF=FA， ∵网格是等边三角形的网格， ∴∠FAB=2×60°=120°， 同理：∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=120°， ∴∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=120°， ∴六边形 ABCDEFA 是正六边形． 最大面积为 24； （3）正六边形的对角线条数为 =9， ∵多边形的外角和是 360°， ∴正六边形的外角和为 360°， 故答案为：9；360°． 第 20页（共 22页） 【点评】此题是正多边形和圆，主要考查了正多边形的定义，正六边形的性质， 网格线的特点，多边形的对角线的确定和多边形的外角和定理，解本题的关键掌 握正六边形的性质． 24．（12 分）阅读理解：（请仔细阅读，认真思考，灵活应用） 【例】已知实数 x 满足 x+ =4，求分式 的值． 解：观察所求式子的特征，因为 x≠0，我们可以先求出 的倒数的值， 因为 =x+3+ =x+ +3=4+3=7 所以 = 【活学活用】 （1）已知实数 a 满足 a+ =﹣5，求分式 的值； （2）已知实数 x 满足 x+ =9，求分式 的值． 【考点】分式的值． 【专题】阅读型；分式． 【分析】（1）原式变形后，将已知等式代入计算即可求出值； （2）原式变形后，将已知等式代入计算即可求出值． 【解答】解：（1）∵a+ =﹣5， ∴ =3a+5+ =3（a+ ）+5=﹣15+5=﹣10； （2）∵x+ =9， ∴x+1≠0，即 x≠﹣1， ∴x+1+ =10， ∵ = =x+1+ +3=10+3=13， ∴ = ． 【点评】此题考查了分式的值，将所求式子就行适当的变形是解本题的关键． 第 21页（共 22页） 25．（14 分）有公共顶点 A 的△ABD，△ACE 都是的等边三角形． （1）如图 1，将△ACE 绕顶点 A 旋转，当 E，C，B 共线时，求∠BCD 的度数； （2）如图 2，将△ACE 绕顶点 A 旋转，当∠ACD=90°时，延长 EC 角 BD 于 F， ①求证：∠DCF=∠BEF； ②写出线段 BF 与 DF 的数量关系，并说明理由． 【考点】三角形综合题． 【分析】（1）先由等边三角形得出 AD=AB，AC=AE，∠DAB=∠CAE=∠E=∠ACE=60°， 从而判断出∠DAC=∠BAE，得到△DAC≌△BAE，最后用平角的定义即可； （2）①同（1）的方法判断出△DAC≌△BAE，再用直角三角形的性质即可； ②作出辅助线，利用①的结论即可得出 DF=BF． 【解答】解：∵△ABD，ACE 都是等边三角形， ∴∠DAB=∠CAE=∠E=∠ACE=60°，AD=AB，AC=AE ∵∠DAC=∠DAB+∠BAC，∠BAE=∠CAE+∠BAC， ∴∠DAC=∠BAE， 在△DAC 和△BAE 中 ， ∴△DAC≌△BAE， ∴∠ACD=∠E=60°， ∵E，C，B 共线， ∴∠BCD=180°﹣∠ACD﹣∠ACE=60°； （2）①∵△ABD，ACE 都是等边三角形， ∴∠DAB=∠CAE=∠E=∠ACE=60°，AD=AB，AC=AE ∵∠DAC=∠DAB﹣∠BAC，∠BAE=∠CAE﹣∠BAC， ∴∠DAC=∠BAE， 第 22页（共 22页） 在△DAC 和△BAE 中 ， ∴△DAC≌△BAE， ∴∠AEB=∠ACD=90°， ∴∠BEC=∠AEB﹣∠AEC=90°﹣60°=30°， ∵∠DCF=180°﹣∠ACD﹣∠ACE=30°， ∴∠DCF=∠BEF； ②DF=BF， 理由：如图， 在 EF 上取一点 G，使 BG=BF， ∴∠GFB=∠FGB， ∴∠DFC=∠BGE， 由（1）知，△DAC≌△BAE，CD=EB， ∠DCF=∠BEC， ∴△DCF≌△BGE， ∴DF=BG， ∴DF=BF． 【点评】此题是三角形综合题，主要考查了等边三角形的性质，全等三角形的判 定和性质，直角三角形的性质，解本题的关键是∠DAC=∠BAE．