数学冀教版八年级上册教案13-3全等三角形的判定（4） 5页

- 1 - 13.3 全等三角形的判定（4） 教学目标 【知识与能力】 1.掌握三角形全等中的两个三角形的特殊位置关系,能利用平移或旋转这两种变换证明两个 三角形全等. 2.能熟练使用三角形全等的判定方法证明两个三角形全等. 【过程与方法】 经历探索的过程,让学生体会平移或旋转这两种变换,培养学生的探究能力和合作精神.. 【情感态度价值观】 通过观察、思考、合作,培养学生不断总结的良好习惯,体会知识间的密切联系. 教学重难点 【教学重点】 “角边角”及“角角边”的内容. 【教学难点】 分析问题,寻找判定两个三角形全等的条件. 课前准备 多媒体课件 教学过程 一、新课导入： 导入一: 1.前面我们学过哪些全等三角形的判定方法?你能用语言叙述出来吗? 【 课 件 1 】 如 图 所 示 , 已 知 ∠ ABC= ∠ DEF,AB=DE, 试 说 明 Δ ABC ≌ Δ DEF. (1)若以“SAS”为依据,还需添加一个条件为 ; (2)若以“ASA”为依据,还需添加一个条件为 ; (3)若以“AAS”为依据,还需添加一个条件为 . 2.思考:一个图形可以进行哪些变换?(平移或旋转) 【 课 件 2 】 你 能 发 现 如 图 所 示 的 两 组 图 形 中 两 个 三 角 形 有 什 么 美 妙 的 关 系 吗 ? - 2 - (甲:将ΔABC 沿直线 BC 平移得到ΔDEF;乙:将ΔABC 绕点 A 旋转 180°得到ΔAED) 议一议: 各图中的两个三角形全等吗? 启示:一个图形经过平移、旋转后,变化了位置,但形状、大小都没有改变,所以平移、旋转前 后的图形全等. [设计意图] 创设情境,激发学生的学习兴趣,让学生体会图形经过平移或旋转后得到的图 形与原图形全等.同时对全等知识的复习有利于学生形成知识网络,为学习新知、掌握图形的 变换与全等的证明打下基础. 导入二: 【教师活动】 提出问题:怎样画出一个图形经过平移或旋转变换后得到的图形? 请你任意画一个三角形,分别画出这个三角形经过平移、旋转后的图形. 【学生活动】 小组内交流、动手操作,利用直尺和量角器等画图形. 师:想一想,平移、旋转后的图形与原图形有怎样的关系? 【学生活动】 组内交流,得出:变换后的图形与原图形形状、大小没有发生变化,两个三角 形全等. 【教师活动】 多媒体演示三角形的平移、旋转两种图形变换,让学生找出相应图形的对应 角和对应边. [设计意图] 通过动手操作,让学生直观感知三角形的全等变换.从中发现规律,得出全等三 角形的特殊位置关系. 导入三: “几何”这个词来源于希腊文,原意是土地测量,真正把几何总结成一门具有严密理论的学科 的是希腊杰出的数学家欧几里得,他非常详尽地搜集了当时所能知道的一切几何事实,写成 了数学史上的早期巨著—《几何原本》.欧几里得的《几何原本》共十三卷,第一卷讲的就是 三角形全等的条件.在几何问题中存在着很多的秘密等待我们去发现和探索,今天我们就来 研究具有平移、旋转等特殊位置关系的全等三角形. [设计意图] 通过史实的介绍激发学生学习的好奇心,让学生积极投入到问题的探究中,加 深对知识探究的欲望. 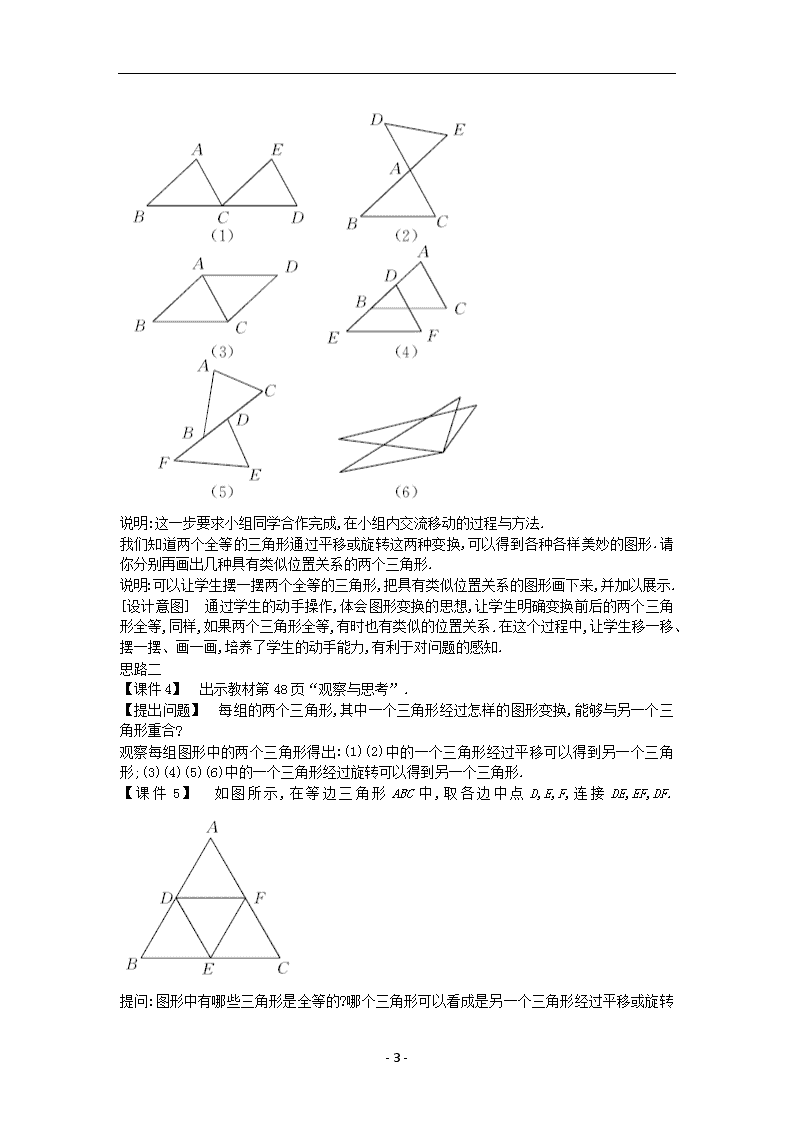二、新知构建： 活动一:感知三角形的全等变换 思路一 【课件 3】 拿一张纸对折后,剪两个全等的三角形,试一试,如果其中一个三角形不动,怎样 移 动 另 一 个 三 角 形 , 能 够 得 到 如 图 所 示 的 各 图 形 . - 3 - 说明:这一步要求小组同学合作完成,在小组内交流移动的过程与方法. 我们知道两个全等的三角形通过平移或旋转这两种变换,可以得到各种各样美妙的图形.请 你分别再画出几种具有类似位置关系的两个三角形. 说明:可以让学生摆一摆两个全等的三角形,把具有类似位置关系的图形画下来,并加以展 示. [设计意图] 通过学生的动手操作,体会图形变换的思想,让学生明确变换前后的两个三角 形全等,同样,如果两个三角形全等,有时也有类似的位置关系.在这个过程中,让学生移一移、 摆一摆、画一画,培养了学生的动手能力,有利于对问题的感知. 思路二 【课件 4】 出示教材第 48 页“观察与思考”. 【提出问题】 每组的两个三角形,其中一个三角形经过怎样的图形变换,能够与另一个三角 形重合? 观察每组图形中的两个三角形得出:(1)(2)中的一个三角形经过平移可以得到另一个三角 形;(3)(4)(5)(6)中的一个三角形经过旋转可以得到另一个三角形. 【 课 件 5 】 如 图 所 示 , 在 等 边 三 角 形 ABC 中 , 取 各 边 中 点 D,E,F, 连 接 DE,EF,DF. - 4 - 提问:图形中有哪些三角形是全等的?哪个三角形可以看成是另一个三角形经过平移或旋转 得到的? 学生组内交流后派代表发言,得出:图形中的ΔADF,ΔBDE,ΔEFC,ΔDEF 都全等,其中任何一 个三角形都可以看成是由另外三个三角形经过平移或旋转得到的. [知识拓展] 一般来说,两个全等三角形的相互位置关系无论怎样变化,总离不开“转、移、 翻”这三种基本形式,如图所示,各组图形中的两个三角形都是能够完全重合的两个三角形, 它们都是全等三角形. [设计意图] 通过感知三角形平移、旋转,培养学生的观察能力和分类思想;通过对问题的讨 论,充分发挥学生的小组合作精神,培养学生思维的严密性. 活动二:例题讲解 [过渡语] 实际上我们遇到的全等三角形的判定中,发现两个三角形间的平移或旋转关 系,能够得到命题证明的图形,较快地解决问题. 【课件 6】 已知:如图所示,在ΔABC 中,D 是 BC 的中点,DE∥AB,交 AC 于点 E,DF∥AC,交 AB 于点 - 5 - F.求证:ΔBDF≌ΔDCE. 问题 1:观察图形,ΔBDF 和ΔDCE 有怎样的位置关系?可以怎样变换得到? (将ΔBDF 沿 BC 方向向右平移线段 BD 的长度,可使ΔBDF 与ΔDCE 重合) 问题 2:要证明ΔBDF 与ΔDCE 全等,题目中已知和未知的元素是什么?要采用哪种判定方法进 行证明? (由 D 是 BC 的中点,可知 BD=DC,再根据平行得到相应的角相等,最后由“ASA”得到两个三角 形全等) 让学生写出证明过程,注意指导学生的书写要规范. 【课件 7】 已知:如图所示,在ΔABC 中,D,E 分别是 AB,AC 的中点,CF∥AB,交 DE 的延长线于点 F. 求证:DE=FE. 问题 1:观察图形中哪两个三角形具有特殊的位置关系. (观察图形可知,将ΔFCE 绕点 E 逆时针旋转 180 度,它可以和ΔDAE 重合) 问题 2:要证明 DE=FE,需要先证什么? (证明线段相等,可先证ΔDAE≌ΔFCE) 说明:在证线段相等时,如果两条线段不在同一个三角形中,可以证这两条线段所在的两个三 角形全等. 请你结合图形完成证明过程. 让学生总结由例 1、例 2 发现的问题. 在三角形全等证明的过程中,要找到图形中具有平移、旋转这两种位置关系的三角形,找出题 目中的条件,然后再进行证明. [设计意图] 通过例题的设计,让学生发现规律、总结规律,感知知识的形成过程. 三、课堂小结： 1.全等三角形是几何图形全等中的一种,根据全等变换,两个全等三角形有时可以看成是一 个三角形由另一个三角形经过平移或旋转得到.当两个三角形存在这种位置关系时,这两个 三角形就全等. 2.三角形全等的证明,要从图形的各种变换中发现图形全等的特征,善于将复杂的图形拆分 成简单的图形来识别全等三角形,要结合题目的已知条件和结论选择合适的条件证明两个三 角形全等.在证明的过程中要做到步步有据,注意步骤的规范.