北师大版数学初中八年级上册课件-第7章- 复习课 17页

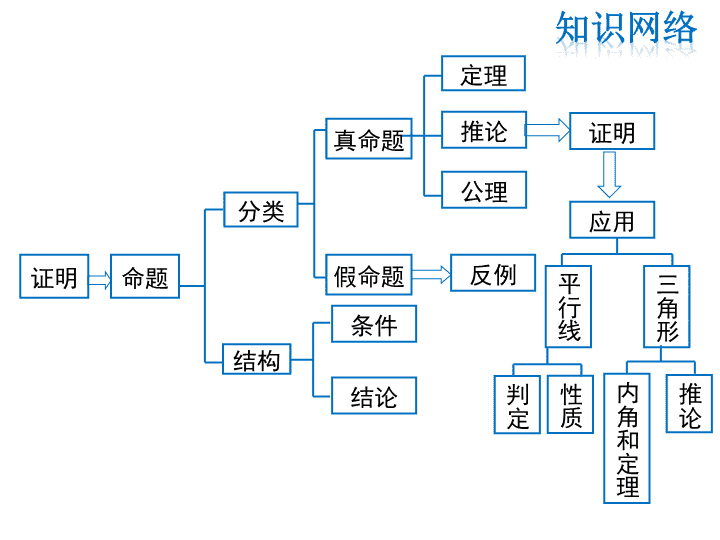
第七章 平行线的证明 复习课 证明 分类 结构 定理 推论 公理 条件 命题 真命题 假命题 结论 反例 证明 应用 平 行 线 三 角 形 判 定 性 质 内 角 和 定 理 推 论 命题 1．判断一件事情的句子叫做命题. 2. 命题有真有假，其中正确的命题叫做　 　；错 误的命题叫做　 　. 真命题 假命题 3. 要说明一个命题是假命题，只要举出一个符合命题 条件，但不符合命题结论的例子就可以，像这样的 例子称为______．反例 1 4.经过实践验证的真命题称为 .基本事实 5. 经过__________得到的重要的真命题叫做________.演绎推理 定理 平行线的判定 图形 已知 结果 结论 同 位 角 内 错 角 同 旁 内 角 21  23  )42( 18042 互补与  a//b a//b a//b 同位角相等 两直线平行 内错角相等 两直线平行 同旁内角互补 两直线平行 1 2 23 24 ） ） ） ） ） ） a b a b a b c c c 2 【公理】 两直线平行,同位角相等. ∵ a∥b, ∴∠1=∠2. 【性质定理1】 两直线平行,内错角相等. ∵ a∥b, ∴∠1=∠2. 【性质定理2】 两直线平行,同旁内角互补. ∵ a∥b, ∴ ∠1+∠2=1800 . a b c 2 1 a b c 1 2 a b c 12 平行线的性质3 三角形内角和定理 【定理】三角形的内角和等于________. 【推论1】三角形的一个外角等于和它不相邻 的两个内角的和. 【推论2】三角形的一个外角大于任何一个和 它不相邻的内角. 180° ４ 1.下列语句是命题的有（ ） （1）两点之间线段最短； （2）向雷锋同志学习； （3）对顶角相等； （4）对应角相等的两个三角形是全等三角形. (1)(3)(4) 2.下列命题，哪些是真命题？哪些是假命题？如 果是真命题，请写出条件与结论，如果是假命题， 请举出反例！ （1）同角的补角相等； （2）同位角相等，两直线平行； （3）若|a|=|b|，则a=b； 真 真 假命题，若a=-1,b=1,则|a|=|b|，但a≠b. 3. 如图，AD、BE、CF为△ABC的三条角平分 线,则： ∠1+∠2+∠3=________. 1 A B C D EF 2 3 90º 4. 如图所示，△ABC中，∠ACD=115°，∠B=55°, 则∠A= , ∠ACB=______ 5. 如图，已知 AB∥CD，若∠ABE=130°, ∠CDE=152°，则∠ BED=______. 60º 65º 78º 第4题 A B C D A B C D EF 第5题 6.如图，直线a,b被直线c所截，a∥b. 求证：∠1+∠2=180°. 证明：∵a∥b（已知）, ∴∠1+∠3=180°（两直线平行，同旁内角互补）. ∵∠3=∠2（对顶角相等）, ∴∠1+∠2=180°(等量代换). 7. 如图，已知∠1+∠2=180°， 求证：∠3=∠4. 证明：∵∠2=∠5（对顶角相等）, ∠1+∠2=180°（已知）, ∴∠1+∠5=180°（等量代换）, ∴CD∥EF（同旁内角互补，两直线平行）, ∴∠3=∠4（两直线平行，同位角相等）. 8.如图，直线AB∥ED. 求证：∠ABC+∠CDE=∠BCD. 证法一：如图，过点C作CF∥AB. A B C DE ∴∠ABC=∠BCF（两直线平行，内错角相等）. ∵AB∥ED（已知）, ∴ED∥CF（平行于同一直线的两条直线互相平行）, ∴∠EDC=∠FCD（两直线平行，内错角相等）, ∴∠BCF+∠FCD=∠EDC+∠ABC（等式性质）, 即∠BCD=∠ABC+∠CDE. F 证法二：如图，延长BC交DE于点G. A B C DE G ∵AB∥DE（已知）, ∴∠ABC=∠CGD（两直线平行，内错角相等）. ∵∠BCD是△CDG的一个外角（外角定义）, ∴∠BCD=∠CGD+∠CDE（三角形的外角定理1）, ∴∠BCD=∠ABC+∠CDE（等量代换）． 9.如图，直线AB∥ED，∠ABC 、∠CDE 、∠BCD之间有什 么数量关系？请说明理由. 如图，过点C作CF∥AB, A B C DE ∴∠ABC + ∠BCF = 180° (两直线平行，同旁内角互补). ∵AB∥ED（已知）, ∴ED∥CF（平行于同一直线的两条直线互相平行）, ∴∠EDC + ∠DCF = 180° (两直线平行，同旁内角互补), ∴∠ABC+∠CDE +∠BCD=∠ABC +∠BCF +∠CDE +∠DCF 解：∠ABC+∠CDE +∠BCD =360°，理由是： F =180°+ 180°=360°(等式性质). 即∠ABC+∠CDE +∠BCD =360°. A B C DE 10.如图，直线AB∥ED，∠ABC 、∠CDE 、∠BCD 之间有什么数量关系？请说明理由. 解：∠ABC = ∠CDE +∠BCD ，理由是： ∵AB∥DE（已知） ∴∠ABC=∠CFE（两直线平行，同位角相等） ∵∠CFE是△CDF的一个外角（外角定义） ∴∠CFE=∠CDE+∠BCD（三角形的外角定理1） ∴∠ABC=∠CDE+∠BCD（等量代换）． F