人教版八年级下册数学导学案 第二十章 数据的代表 6页

第二十章 数据的代表 第一课时 平均数、中位数、众数 1.平均数是代表一组数据平均水平的量，小数我们学习的平均数的求法，数据中每一个数据 的重要性是一样的。它等于这些数据的和除经这些数据的个数。 例如： 求这组数据的平均数，12，10，14，5，  4 40 4 4141012x 2.加权平均数，权就是对一组数据中的每一个数的权限，加权平均数的应用非常广泛，主要 用于面试、各小组数据个数不一样的情况平均数的求法。也可说小学数学中平均数的计算方 法只是权为 1：1：1：1 的特殊情况。 例如： 12，10，14，5，还是这组数据，如果权不是 1：1：1：1，改为：1：2：3：4 那这时的加权 平均数就应该为： 10 20422012 4321 45314210112  x = 这里，1，2，3，4，分别的对 12，10，14，5 数据的一个权限。就可说是一共有 10 份，计算 每一份的多少，而不是 4 份。 3 中位数是代表一组数据中间水平的一个数学量，计算出中位数就能知道，这组数据中有一 半的数是大于这个数，而有一半的数小于这个数。 4.计算中位数时，先要对这组数据排列好大小顺序，（从大到小或从小到大）然后确定数据的 个数，如果是奇数个，那就是中间这个数，如果的偶数个，那应该是中间两个数的平均数。 例如： 12，25，10，36，50，18，5 排序为： 5，10，12，18，25，36，50， 中间数为第四个数，所以中位数为 18。 12，25，10，36，50，18，5，22 排序为： 5，10，12，18，22，25，36，50， 中间数应该为第四和第五两个，那么中位数为：  2 2218 所以中位数应该为： 5.如果是一组数据的个数比较多，那中间那个数的位置应该怎样判断呢？下而介绍方法----填 空法。 数据个数为奇数时：例如 101 个从大到小排好序好的数，那中间一个数应该是第多少个呢？ 前 （中间位置 1 个） 后 减去中间那一个，还有 100 个，所以前应该有 50 个，后也应该有 50 个，所以中位数应该为第 51 个。 数据个数为偶数时：例如 200 个排序好的数，那中位数应该是中间两个数的平均数。 前 （中间位置 2 个） 后 减去中间位置 2 个，还有 188 个，那就是前 94 个 后 94 个，中间位置为第 95 和第 96 个。中位数为这两个数的平均数。 6 众数代表一组数据出现次数最多量，多数用于市场调查，例如哪种码样的鞋卖得多，这就 是计算众数，对商品的进货有很好的指导作用。 计算方法：一组数据中出现次数最多的这个数，如果一组数据中有多个数出现的次数一样， 那它们都是这个数的众数，所以中位数只能有一个而众数却可能有多个。 例如 6 12 24 6 0 5 10 15 20 25 做成7件 做成8件 做成9件 做成10件 12 ，12，14，1，15，14，17，14，19，15，18，14 众数为：14 因为它出现了 次。 一.填空题 1. 评定学生的学科期末成绩由期考分数, 作业分数, 课堂参与分数三部分组成, 并按 3:3:4 的比例确定. 已知小明的数学期考 80 分, 作业 90 分, 课堂参与 85 分, 则他的数学期 末成绩为. 2. 某校八年级⑶班在一次数学测验中,有 2 人得 100 分,4 人得 95 分,2 人得 90 分,6 人得 85 分,4 人得 80 分,6 得 75 分,5 人得 72 分,5 人得 64 分,4 人得 60 分,4 人得 55 分,2 人得 50 分,6 人得 40 分,则该班的数学成绩平均为分. 3. 数据 –2,0,2,3,4,2,5 的中位数是. 4. 数据 9,6,4,4,5,6,7,6,8,6 的众数是,中位数是,平均数是. 5. 某校八年级⑷班 47 人,身高 1.70 米的有 10 人,1.66 米的有 5 人,1.6 米的有 15 人,1.58 米的有 10 人,1.55 米的有 5 人,1.50 米的有 2 人,则该班学生的身高的平均数为,中位数为, 众数为. 6．一个射手连续射靶 20 次，其中 2 次射中 10 环，7 次射中 9 环，8 次射中 8 环，3 次射中 7 环，那么，这个射手中靶的环数的平均数是_______（保留一位小数），众数是_____，中位 数是_______． 7．某养鱼专业户，在捕捞前，随意捞出 10 尾鱼，称得这 10 尾鱼的重量如下（单位：kg）： 0.8，0.9，1.2，1.3，0.8，0.9，1.1，1.0，1.2，0.8，则这 10 尾鱼重量数的中位数是， 众数是． 8. 若数据 4,6,x,8,12 的平均数为 8,则其中位数为. 9. 若数据 5,-3,0,x,4,6 的中位数为 4,则其众数为. 10．某旅行社组甲、乙两个团，两团游客的年龄如下（单位：岁） 甲：13 13 14 15 15 15 15 16 17 17 乙：3 4 4 5 5 6 6 6 54 57 （1）甲团游客的平均年龄是岁，中位数是，众数是，其中能较好反映本团游客年龄特征的是。 （2）乙团游客的平均年龄是岁，中位数是，众数是，其中能较好反映本团游客年龄特征的是。 11．综合实践活动中，同学们做泥塑工艺制作。二黑将活动组同学的作品完成情况绘成了下 面的条形统计图．根据图表，我们可以知道平均每个学生完成作品件。这些作品的中位数是 件。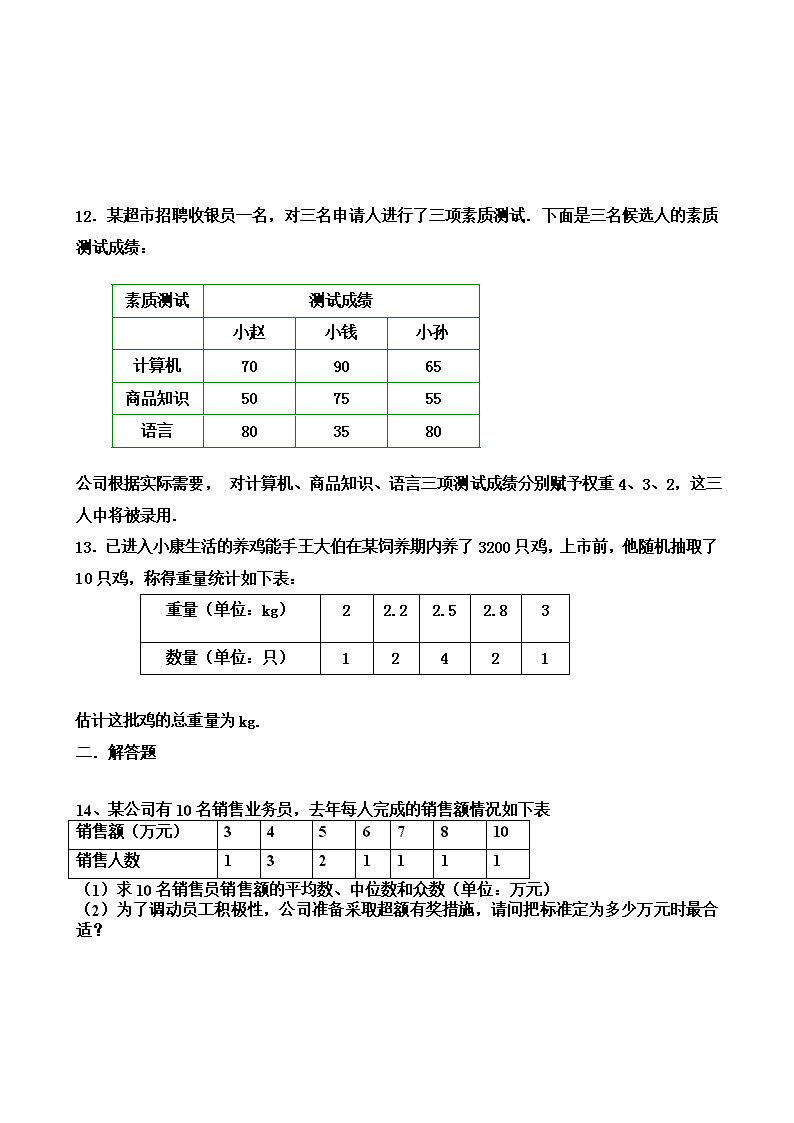 12．某超市招聘收银员一名，对三名申请人进行了三项素质测试．下面是三名候选人的素质 测试成绩： 素质测试 测试成绩 小赵 小钱 小孙 计算机 70 90 65 商品知识 50 75 55 语言 80 35 80 公司根据实际需要， 对计算机、商品知识、语言三项测试成绩分别赋予权重 4、3、2，这三 人中将被录用. 13．已进入小康生活的养鸡能手王大伯在某饲养期内养了 3200 只鸡，上市前，他随机抽取了 10 只鸡，称得重量统计如下表： 重量（单位：kg） 2 2.2 2.5 2.8 3 数量（单位：只） 1 2 4 2 1 估计这批鸡的总重量为 kg. 二．解答题 14、某公司有 10 名销售业务员，去年每人完成的销售额情况如下表 销售额（万元） 3 4 5 6 7 8 10 销售人数 1 3 2 1 1 1 1 （1）求 10 名销售员销售额的平均数、中位数和众数（单位：万元） （2）为了调动员工积极性，公司准备采取超额有奖措施，请问把标准定为多少万元时最合适？ 15、随机抽取某城市一年(365 天计算)中的 30 天的日平均气温状况统计如下表: (1) 该组数据的中位数是_________,众数是__________; (2) 该城市一年中日平均气温为 26℃的约有_________天; (3) 若日平均气温在 17℃-23℃为市民”满意温度”,则该市一年中达到市民”满意温度”的 约有_______天. 第二课时 极 差、方差 1.极差中“极”是例如地理中的南极、北极等，因此极差的故名意思为，一组数据中最大值 与最小值的差。 2.方差代表的是一组数据的波动情况，也就是每一个数据相对平均数的情况，方差越大波动 越大数据越，方差越小波动越小，数据越 ， 3.方差的计算方法： n xxxxxxs n 22 2 2 12 )(.......)()(  4.标准差 n xxxxxxss n 22 2 2 12 )(.......)()(  一、选择题（每题 5 分，共 30 分） 1.若一组数据 1，2，3，x 的极差为 6，则 x 的值是（ ） 温 度 / ℃ 10 14 18 22 26 30 32 天 数 / 天 3 5 5 7 6 2 2 A．7 B．8 C．9 D．7 或－3 2.一组数据 13，14，15，16，17 的标准差是（ ） A.0 B.10 C. 2 D.2 3 下列统计量中，能反映一名同学在 7～9 年级学段的学习成绩稳定程度的是（ ） A．平均数 B．中位数 C．众数 D．方差 4.人数相等的甲.乙两班学生参加了同一次数学测验，班级平均分和方差如下： 甲x =80， 乙x =80，s 2 甲 =240，s 2 乙 =180，则成绩较为稳定的班级为 （ ） A.甲班 B.乙班 C.两班成绩一样稳定 D.无法确定 5.在甲.乙两块试验田内，对生长的禾苗高度进行测量，分析数据得：甲试验田内禾苗高度 数据的方差比乙实验田的方差小，则（ ） A.甲试验田禾苗平均高度较高 B．甲试验田禾苗长得较整齐 C.乙试验田禾苗平均高度较高 D．乙试验田禾苗长得较整齐 6．计算一组数据：8，9，10，11，12 的方差为（ ） A．1 B．2 C．3 D．4 7．甲、乙二人在相同情况下，各射靶 10 次，两人命中环数的平均数 x 甲= x 乙=7， 方差 S 甲 2=3，S 乙 2=1.2，则射击成绩较稳定的是（ ） A．甲 B．乙 C．一样 D．不能确定 8．甲、乙两八年级学生在一学期里多次检测中，其数学成绩的平均分相等，但他们成绩的 方差不等，那么正确评价他们的数学学习情况的是（ ） A．学习水平一样 B．成绩虽然一样，但方差大的学生学习潜力大 C．虽然平均成绩一样，但方差小的学习成绩稳定 D．方差较小的学习成绩不稳定，忽高忽低 9.已知甲.乙两组数据的平均数相等，若甲组数据的方差 2s 甲 ＝0.055，乙组数据的方差 2s 乙 ＝ 0.105，则（ ） A．甲组数据比乙组数据波动大 B．乙组数据比甲组数据波动大 C．甲组数据与乙组数据的波动一样大 D．甲.乙两组数据的数据波动不能比较 10、如果将一组数据的每一个数据扩大 2 倍，那么平均数 （ ） A. 不变 B. 扩大 2 倍 C. 缩小 2 倍 D.无法确定 11、如果将一组数据的每一个数据扩大 2 倍，那么方差 （ ） A. 不变 B. 扩大 4 倍 C. 缩小 4 倍 D.无法确定 12、如果将一组数据的每一个数据扩大 2 倍，那么标准差 （ ） A. 不变 B. 扩大 2 倍 C. 缩小 2 倍 D.无法确定 13.在方差的计算公式 s 2 = 10 1 [（x 1 -20） 2 +（x 2 -20） 2 +……+（x 10 -20） 2 ]中，数字 10 和 20 分别表示的意义可以是 （ ） A.数据的个数和方差 B.平均数和数据的个数 C.数据的个数和平均数 D.数据组的方差和平均数 14.如图是甲.乙两位同学 5 次数学考试成绩的折线统计图，你认为成绩较稳定的是（ ） A.甲 B.乙 C.甲.乙的成绩一样稳定 D.无法确定 二．填空题 15.已知一个样本的方差 2 2 2 2 1 2 1 [( 6) ( 6) ( 6) ]11 nS x x x       ，则这个样本的容量是 ____________，样本的平均数是_____________. 16．（2006，长春市）5 名同学目测同一本教科书的宽度时，产生的误差如下（单位：cm）： 2，-2，-1，1，0，则这组数据的极差为______cm． 17．一组数据-8，-4，5，6，7，7，8，9的极差是______，方差是_____，标准差是______． 18.已知数据 a.b.c 的方差是 1，则 4a，4b，4c 的方差是. 三、解答题（共 28 分） 19.（8 分）某学生在一学年的 6 次测验中语文.数学成绩分别为（单位：分）： 语文：80，84，88，76，79，85 数学：80，75，90，64，88，95 试估计该学生是数学成绩稳定还是语文成绩稳定？