北师大版数学八年级下册特殊三角形 课后练习 6页

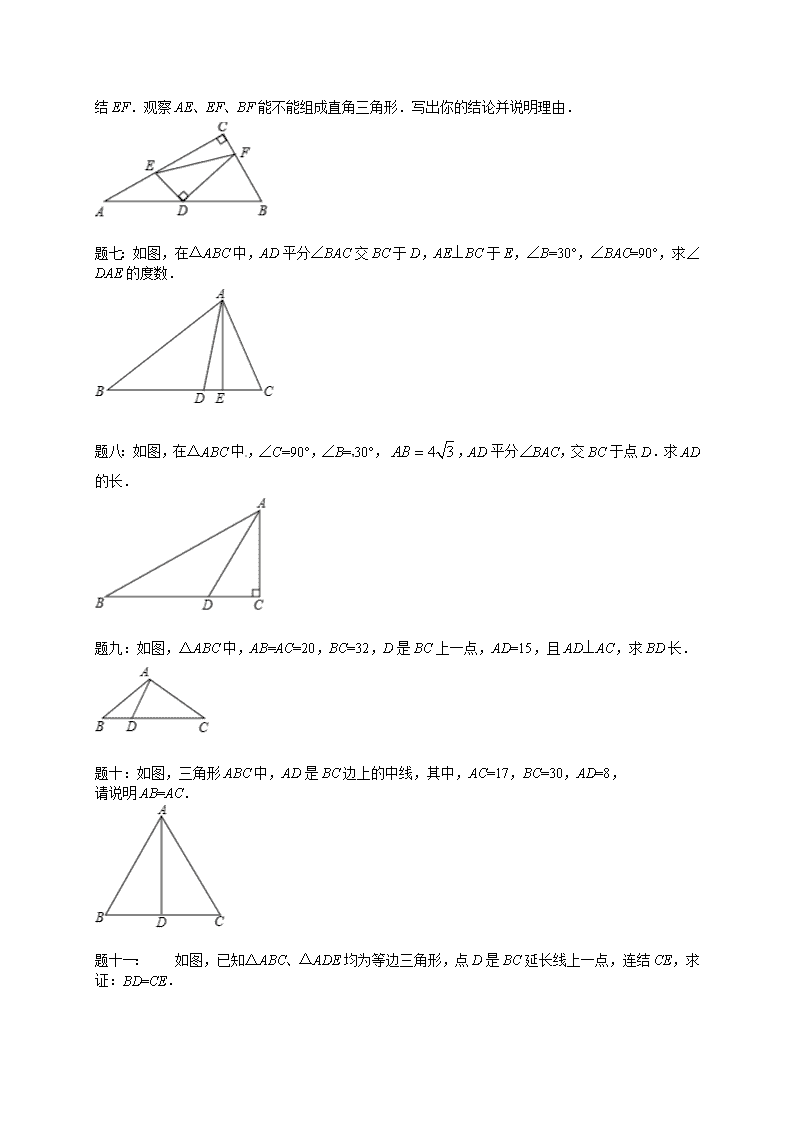
特殊三角形课后练习 主讲教师：傲德 题一：如图，已知 AB=AC，AD=AE．求证：BD=CE． 题二：如图，点 D，E 分别在 AB，AC 上，且 AD=AE，∠BDC=∠CEB．求证：BD=CE． 题三：如图，已知等边△ABC 的边长为 2，BD 是 AC 边上的中线，E 为 BC 延长线上一点，且 CD=CE， 则 DE= ． 题四：如图，已知等边△ABC 的周长为 6，BD 是 AC 边的中线，E 为 BC 延长线上一点，CD=CE， 那么△BDE 的周长是 ． 题五：如图，大小不等、形状相同的两个三角 板（等腰直角）△OAB 和△EOF 摆拼在一起，它们的 直角顶点重合，连结 AE、BF，你认为线段 AE、线段 BF 有怎样的关系？证明你的结论． 题六：如图，在直角△ABC 中，D 为斜边 AB 的中点，DE⊥DF，而 E、F 分别在 AC 和 BC 上，连 结 EF．观察 AE、EF、BF 能不能组成直角三角形．写出你的结论并说明理由． 题七：如图，在△ABC 中，AD 平分∠BAC 交 BC 于 D，AE⊥BC 于 E，∠B=30°，∠BAC=90°，求∠ DAE 的度数． 题八：如图，在△ABC 中，∠C=90°，∠B= 30°， 4 3AB  ，AD 平分∠BAC，交 BC 于点 D．求 AD 的长． 题九：如图，△ABC 中，AB=AC=20，BC=32，D 是 BC 上一点，AD=15，且 AD⊥AC，求 BD 长． 题十：如图，三角形 ABC 中，AD 是 BC 边上的中线，其中，AC=17，BC=30，AD=8， 请说明 AB=AC． 题十一：如图，已知△ABC、△ADE 均为等边三角形，点 D 是 BC 延长线上一点，连结 CE，求证： BD=CE． 题十二：已知：如图，△ABC、△CDE 都是等边三角形，AD、BE 相交于点 O，点 M、N 分别是线 段 AD、BE 的中点．（1）求证：AD=BE；（2）求证：△MNC 是等边三角形． 题十三：已知 三个实数 a、b、c 满足 a+b+c=0，abc=1，求证：a、b、c 中至少有一个大于 3 2 ． 题十四：平面上有 A、B，C、D 四点，其中任何三点都不在一直线上． 求证：在△ABC、△ABD、△ACD、△BDC 中至少有一个三角形的内角不超过 45°． 特殊三角形 课后练习参考答案 题一： 见详解． 详解：证明：作 AF⊥BC 于 F，∵AB=AC（已知），∴BF=CF（三线合一）， 又∵AD=AE（已知），∴DF=EF（三线合一），∴BFDF=CFEF，即 BD=CE（等式的性质）． [来源:www.shulihua.net] 题二： 见详解． 详解：∵∠ADC+∠BDC=180°，∠BEC+∠AEB=180°，又∵∠BDC=∠CEB， ∴∠ADC=∠AEB．在△ADC 和△AEB 中， ( ( A A AD AE ADC AEB         公共角） （已知） 已证） ，∴△ADC≌△AEB（ASA）．∴AB=AC． ∴ABAD=ACAE．即 BD=CE． 题三： 3 ． 详解：∵△ABC 是边长为 2 的等边三角形，BD 是 AC 边上的中线， ∴∠ACB=60°，BD⊥AC，BD 平分∠ABC， 01 302DBE ABC    ， ∴ 0 3sin 60 2 32BD BC     ，∵CD=CE，∴∠CDE=∠E． ∵∠ACB=60°，且∠ACB 为△CDE 的外角，∴∠CDE+∠E=60°， ∴∠CDE=∠E=30°， ∴∠DBE=∠DEB=30°，∴ 3BD DE  ，故答案为： 3 ． 题四： 3 2 3 ． 详解：△ABC 的周长为 6，∴AB=BC=AC=2，DC=CE=1， 又∵∠ACB=∠CDE+∠CED，∴∠CED=30°，△BDE 为等腰三角形， 3DE BE  ，∴ 2 3 2 1 3 2 3DE BE BD       ， 故答案为 3 2 3 ． 题五： AE=BF，AE⊥BF．[来源:数理化网] 详解：AE=BF，AE⊥BF，证明：∵△AOB 和△EOF 是等腰直角三角形， ∴OA=OB，OE=OF，∠AOB=∠EOF=90°，∴∠AOB∠EOB=∠EOF∠EOB， ∴∠AOE=∠BOF，在△AOE 和△BOF 中， AO BO AOE BOF OE OF       ， ∴△AOE≌△BOF（SAS），∴AE=BF，∠EAO=∠FBO， 延长 AE 交 OB 于 M，交 BF 于 H，∵∠AMO=∠BMH，∠EAO=∠FBO， ∴∠BHM=∠AOM=90°，∴AE⊥BF． 题 六 ： 能组成直角三角形，斜边为 EF． 详解：如图，延长 FD 到 F′，使 DF′=DF，连接 AF′、EF′，∵D 为斜边 AB 的中点， ∴AD=BD，[来源:www.shulihua.net] 在△ADF′和△BDF 中， AD BD ADF BDF DF DF       ，∴△ADF′≌△BDF（SAS）， ∴AF′=BF，∠B=∠DAF′，∵∠BAC+∠B=90°，∴∠BAC+∠DAF′=∠BAC+∠B=90°， 即∠EAF′=90°，又∵DE⊥DF，∴EF′=EF，∴△EAF′是以 EF′为斜边的直角三角形，[来源:www.shulihua.net 数理化网] 故 AE、EF、BF 能组成直角三角形，斜边为 EF． 题七： 15°． 详解：∵AD 平分∠BAC，∠BAC=90°，∴∠BAD=45°，∵AE⊥BC，∴∠AEB=90° ∵∠B=30°，∠BAE+∠B+∠AEB=180°，∴∠BAE=60°， ∴∠DAE=∠BAE∠BAD=60°45°=15°，答：∠DAE 的度数为 15°． 题八： 4． 详解：在 Rt△ABC中，∠B=30°， 4 3AB  ，∴ 1 2 32AC AB  ，∠BAC=60°， 又∵AD 平分∠BAC，∴ 01 30 , 2 32DAC BAC AC     ，∴ 3 23DC AC  ， AD=2DC=4．所以 AD 的长为 4． 题九： 7． 详解：∵AD⊥AC，AC=20，AD=15，∴ 2 220 15 25CD    ， ∴BD=BCCD=3225=7． 题十： 见详解． 详解： 1 152CD BC  ，∵CD2+AD2=225+64=2 89=AC2，∴三角形 ADC 是直角三角形，且∠ADC 是直角．∵AD 既是 BC 边中线，又是 BC 边垂线，∴三角形 ABC 是等腰三角形，且 AB=AC． 题十一： 见详解． 详解：∵△ABC、△ADE 均为等边三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=60°，∴∠BAC+∠CAD=∠DAE+∠CAD， ∴∠BAD=∠CAE，在△ABD 和△ACE 中， AB AC BAD CAE AD AE       ，∴△ABD≌△ACE（SAS），∴BD=CE． 题十二： 见详解． 详解：（1）∵△ABC、△CDE 都是等边三角形，∴AC=BC，CD=CE，∠ACB=∠DCE=60°，∵∠ACB+∠BCD=∠ACD， ∠DCE+∠BCD=∠BCE，∴∠ACD=∠BCE， 在△ACD 和△BCE 中， AC BC ACD BCE CD CE       ，∴△ACD≌△BCE（SAS），∴AD=BE； （2）∵△ACD≌△BCE，∴∠CAD=∠CBE，∵点 M、N 分别是线段 AD、BE 的中点，AD=BE，∴AM=BN，在△ACM 和△BCN 中， AC BC CAD CBE AM BN       ， ∴△ACM≌△BCN（SAS），[来源:www.shulihua.net] ∴CM=CN，∠ACM=∠BCN，∴∠MCN=∠BCM+∠BCN=∠BCM+∠ACM=∠ACB=60°，∴△MNC 是等边三角形． 题十三： 见详解 详解：∵a+b+c=0，∴a、b、c 必有一个正数，不妨设 c＞0，a+b=c， 1ab c  ． 这样 a、b 可看作方程 2 1 0x cx c    的两实根． 2 14 0c c      ，即 3 327 27 34 ,8 8 2c c     ．所以 a、b、c 中至少有一 个大于 3 2 ． 题十四： 见详解 详解：假设 A、B，C、D 四点，任选三点构成的三角形的三个内角都大于 45°， 当 ABCD 构成凸四边形时，可得各角和大于 360°，与四边形内角和等于 360°矛盾； 当 ABCD 构成凹四边形时，可得三角形内角和大于 180°，与三角形内角和等于 180°矛盾． 故在△ABC、△ABD、△ACD、△BDC 中至少有一个三角形的内角不超过 45°．