【同步作业】人教版 八年级下册数学第十八章 平行四边形 复习1（含答案） 6页

第 1 页 共 6 页 《平行四边形》复习 一、选择题： 1、下列给出的条件中，能判断四边形 ABCD 是平行四边形的是( ) A.AB∥CD，AD = BC； B.∠B = ∠C；∠A = ∠D， C.AB =CD，CB = AD； D.AB = AD，CD = BC 2、矩形具有而菱形不具有的性质是（ ） A.两组对边分别平行 B.对角线相等 C.对角线互相平分 D.两组对角分别相等 3、如图,下列四组条件中，能判定□ABCD 是正方形的有( ) ①AB=BC，∠A=90°；②AC⊥BD，AC=BD；③OA=OD，BC=CD；④∠BOC=90°，∠ABD=∠DCA. A．1 个 B．2 个 C．3 个 D．4 个 4、如图，在▱ ABCD 中，CE⊥AB，且 E 为垂足．如果∠D=75°，则∠BCE=（ ） A.105° B.15° C.30° D.25° 第 4 题图 第 5 题图 第 6 题图 5、如图，▱ ABCD 的对角线 AC 与 BD 相交于点 O，AB⊥AC，若 AB=4，AC=6，则 BD 的长是 （ ） A．8 B．9 C．10 D．11 6、如图，Rt△ABC 中，∠C=90°，CD⊥AB 于 D，E 是 AC 的中点，则下列结论中一定正确的 是( ) A．∠4=∠5 B．∠1=∠2 C．∠4=∠3 D．∠B=∠2 7、如图，已知 AC、BD 是菱形 ABCD 的对角线，那么下列结论一定正确的是（ ） A.△ABD 与△ABC 的周长相等 B.△ABD 与△ABC 的面积相等 C.菱形的周长等于两条对角线之和的两倍 D.菱形的面积等于两条对角线之积的两倍 第 2 页 共 6 页 第 7 题图 第 8 题图 第 9 题图 8、如图,在△ABC 中,∠ACB=90°,∠ABC=60°,BD 平分∠ABC,P 点是 BD 中点,若 AD=6,则 CP 长为（ ） A.3 B.3.5 C.4 D.4.5 9、如图，在矩形 ABCD 中，AB=2，BC=4，对角线 AC 的垂直平分线分别交 AD、AC 于点 E、O， 连接 CE，则 CE 的长为（ ） A．3 B．3.5 C．2.5 D．2.8 10、如图，在菱形 ABCD 中，对角线 AC=6，BD=8，点 E、F 分别是边 AB、BC 的中点，点 P 在 AC 上运动，在运动过程中，存在 PE+PF 的最小值，则这个最小值是（ ） A．3 B．4 C．5 D．6 第 10 题图 第 11 题图 第 12 题图 11、如图,在菱形 ABCD 中,菱形 ABCD 面积为 12 3 ，∠B=60°，则以 AC 为边长正方形 ACEF 边长为（ ） A.2 3 B.2 2 C.2 6 D.6 12、如图，在正方形 ABCD 中，边长为 2 的等边三角形 AEF 的顶点 E、F 分别在 BC 和 CD 上．下 列结论：①CE=CF；②∠AEB=75°；③BE+DF=EF；④S 正方形 ABCD=2+ ．其中正确的个数为 （ ） A．1 B．2 C．3 D．4 二、填空题: 13、如图，四边形 ABCD 是矩形，则只须补充条件 （用字母表示只 添加一个条件）就可以判定四边形 ABCD 是正方形. 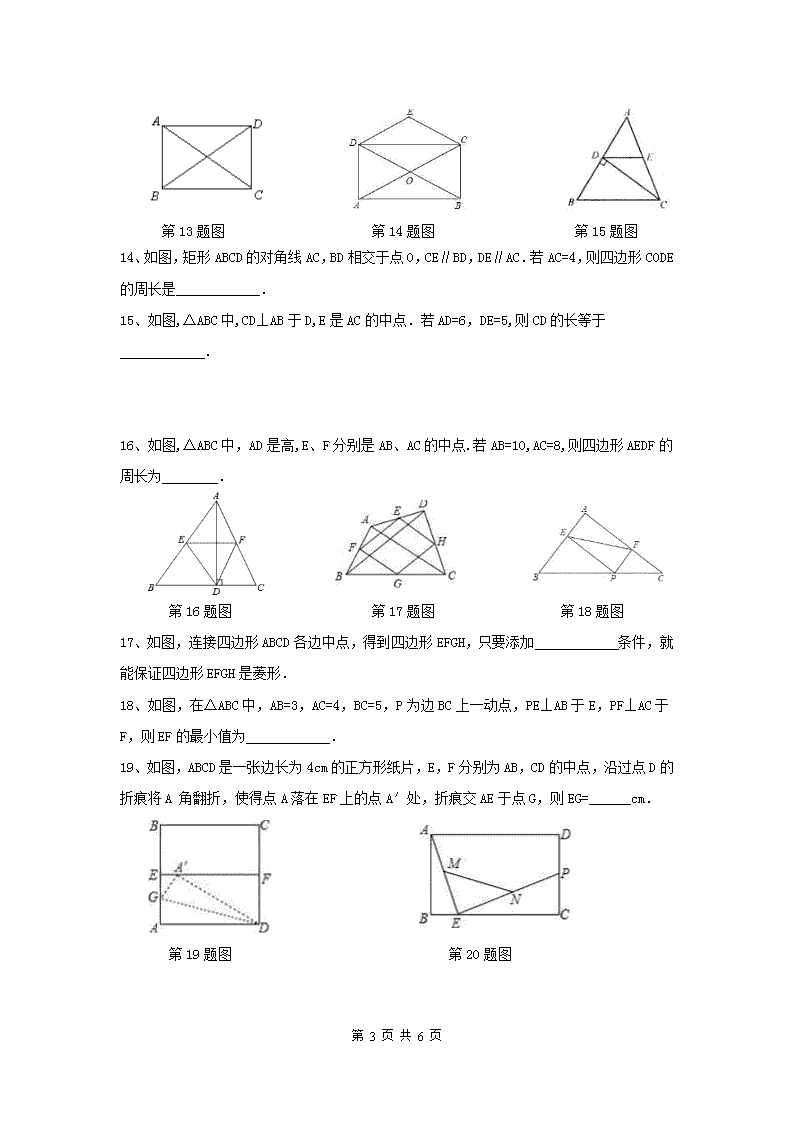第 3 页 共 6 页 第 13 题图 第 14 题图 第 15 题图 14、如图，矩形 ABCD 的对角线 AC，BD 相交于点 O，CE∥BD，DE∥AC．若 AC=4，则四边形 CODE 的周长是 ． 15、如图,△ABC 中,CD⊥AB 于 D,E 是 AC 的中点．若 AD=6，DE=5,则 CD 的长等于 ． 16、如图,△ABC 中，AD 是高,E、F 分别是 AB、AC 的中点.若 AB=10,AC=8,则四边形 AEDF 的 周长为 ． 第 16 题图 第 17 题图 第 18 题图 17、如图，连接四边形 ABCD 各边中点，得到四边形 EFGH，只要添加 条件，就 能保证四边形 EFGH 是菱形． 18、如图，在△ABC 中，AB=3，AC=4，BC=5，P 为边 BC 上一动点，PE⊥AB 于 E，PF⊥AC 于 F， 则 EF 的最小值为 ． 19、如图，ABCD 是一张边长为 4cm 的正方形纸片，E，F 分别为 AB，CD 的中点，沿过点 D 的折痕将 A 角翻折，使得点 A 落在 EF 上的点 A′处，折痕交 AE 于点 G，则 EG=______cm． 第 19 题图 第 20 题图 20、如图，矩形 ABCD 中，AB=6，BC=8，E 是 BC 边上的一定点，P 是 CD 边上的一动点（不与 点 C、D 重合），M，N 分别是 AE、PE 的中点，记 MN 的长度为 a，在点 P 运动过程中，a 不 断变化，则 a 的取值范围是 ． 第 4 页 共 6 页 三、简答题: 21、如图，已知 E，F 是▱ ABCD 的对角线 AC 上的两点，BE∥DF，求证：AF=CE． 22、如图，点 E、F 为线段 BD 的两个三等分点，四边形 AECF 是菱形． （1）试判断四边形 ABCD 的形状，并加以证明； （2）若菱形 AECF 的周长为 20，BD 为 24，试求四边形 ABCD 的面积． 23、如图，在△ABC 中，CF⊥AB，BE⊥AC，M、N 分别是 BC、EF 的中点，试说明 MN⊥EF． 第 5 页 共 6 页 24、如图，四边形 ABCD 为矩形（对边相等，四个角是直角），过点 D 作对角线 BD 的垂线， 交 BC 的延长线于点 E，在 BE 上取一点 F，使 DF=EF=4．设 AB=x，AD=y，求代数式 的值． 参考答案 第 6 页 共 6 页 1、C 2、B． 3、D 4、B． 5、C． 6、A． 7、B 8、A 9、C． 10、C． 11、D． 12、 C． 13、略 14、答案为：8． 15、答案为：8；16、答案为：18．17、答案为：AC=BD． 18、答案为：2.4．19、答案为：4 ﹣6．20、答案为：4＜a＜5 ． 21、【解答】证明：在平行四边形 ABCD 中，∵AD∥BC，AD=BC，∴∠ACB=∠CAD． 又∵BE∥DF，∴∠BEC=∠DFA，在△BEC 与△DFA 中， ，∴△BEC≌△DFA，∴ AF=CE． 22、【解答】解：（1）四边形 ABCD 为菱形．理由如下：如图，连接 AC 交 BD 于点 O， ∵四边形 AECF 是菱形，∴AC⊥BD，AO=OC，EO=OF， 又∵点 E、F 为线段 BD 的两个三等分点，∴BE=FD，∴BO=OD， ∵AO=OC，∴四边形 ABCD 为平行四边形，∵AC⊥BD，∴四边形 ABCD 为菱形； （2）∵四边形 AECF 为菱形，且周长为 20，∴AE=5，∵BD=24，∴EF=8，OE= EF= ×8=4， 由勾股定理得，AO= = =3，∴AC=2AO=2×3=6，∴S 四边形 ABCD= BD•AC= × 24×6=72． 23、【解答】证明：连接 MF、ME， ∵CF⊥AB，在 Rt△BFC 中，M 是 BC 的中点，∴MF= BC（斜边中线等于斜边一半）， 同理 ME= BC，∴ME=MF，∵N 是 EF 的中点，∴MN⊥EF． 24、【解答】解：由题意知：AB=CD=x，AD=BC=y，CD⊥BE， ∵BD⊥DE，∴∠BDF+∠FDE=90°∠DBF+∠E=90°， ∵DF=EF，∴∠E=∠FDE，∴∠BDF=∠DBF，∴DF=BF=4，∴CF=4﹣x， 在 Rt△CDF 中 ，∴ = ．