北师大版数学初中八年级上册课件-第3章-3平面直角坐标系 27页

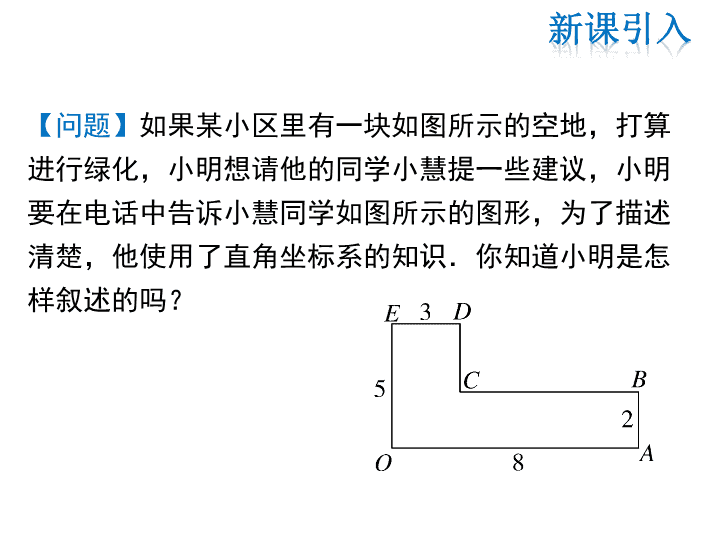
第三章 位置与坐标 3.2 平面直角坐标系 第2课时 建立平面直角坐标系确定点的坐标 学习目标 1.了解、掌握点的坐标及特殊位置上点的坐标特 征；（重点） 2.能建立直角坐标系求点的坐标.（难点） 【问题】如果某小区里有一块如图所示的空地，打算 进行绿化，小明想请他的同学小慧提一些建议，小明 要在电话中告诉小慧同学如图所示的图形，为了描述 清楚，他使用了直角坐标系的知识．你知道小明是怎 样叙述的吗？ 描点及坐标的特点 【问题】我们上节课已经学习过了平面直角坐标系的 定义．根据定义想一想你会在坐标轴上描点吗？ 找点的方法： 先分别找出该点的横坐标、纵坐标在两 条数轴上的点，再分别作对应坐标轴的垂 线，交点即为所要找的点的位置． 1 【例1】在直角坐标系中描出下列各点，并将 各组内的点用线段依次连接起来. ① (-6,5),(-10,3),(-9,3),(-3,3),(-2,3); ② (-9,3),(-9,0),(-3,0),(-3,3); ③ (3.5,9),(2,7),(3,7),(4,7),(5,7); ④ (3,7),(1,5),(2,5),(5,5),(6,5); ⑤ (2,5),(0,3),(3,3),(3,0),(4,0),(4,3),(7,3),(5,5). 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 x y o ●● ● ● ●●● ●●● ● ●● ● ● ● ● ● ● ● ● ● 观察所得图形，你觉得它像什么？ 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 x y o ●● ● ● ●●● ●●● ● ●● ● ● ● ● ● ● ● ● ● 2.线段EC与x轴有 什么位置关系？ 点E和点C的坐标 有什么特点？线 段EC上其它点的 坐标呢？ D F E CB G A 1.图形中哪些点 在坐标轴上，它 们的坐标有什么 特点？ 3.点F和点G的横坐标有什么共同特点？ 线段FG与y轴有怎样的位置关系？ 点的位置 横坐标的 符号 纵坐标的 符号 在x轴的 正半轴上 在x轴的 负半轴上 在y轴的 正半轴上 在y轴的 负半轴上 0 + + - - 0 0 0 A y O x-1-2-3 -1 -2 -3 -4 1 2 3 4 1 2 3 4 5 -4 B C E 与坐标轴平行的直线上的点的坐标特征： (1)与x轴平行的直线上各点的_______坐标都相同； (2)与y轴平行的直线上各点的_______坐标都相同． 纵 横 A y O x-1-2-3 -1 -2 -3 -4 1 2 3 4 1 2 3 4 5 -4 B C 【画一画】你能在直角坐标系里描出点A(-4,-5),B(-2,0), C(4,0)吗？并连线． O x y -5 -4 -3 -2 -1 1 2 3 4 5 4 3 2 1 -1 -2 -3 -4 -5 A B C ● ● ● O x y -5 -4 -3 -2 -1 1 2 3 4 5 4 3 2 1 -1 -2 -3 -4 -5 A B C ● ● ● 【问题】你能求出△ABC的面积吗？ D 解：过点A作AD⊥x轴于点D. ∵A(-4,-5)，∴D(-4,0) . 由点的坐标可得 AD=5 ，BC=6， ∴ S△ABC = ·BC·AD = ×6×5=15. 1 2 1 2 【例2】如图，已知点A(2，－1)，B(4，3)，C(1，2)， 求△ABC的面积． 解：如图，过点A作x轴的平行线，过点C 作y轴的平行线，两条平行线交于点E，过 点B分别作x轴、y轴的平行线，分别交EC 的延长线于点D，交EA的延长线于点F. ∵A(2，－1)，B(4，3)，C(1，2)， ∴BD＝3，CD＝1，CE＝3，AE＝1，AF＝2，BF＝4， ∴S△ABC＝S长方形BDEF－S△BDC－S△CEA－S△BFA ＝BD·DE－ DC·DB－ CE·AE－ AF·BF ＝12－1.5－1.5－4＝5. 1 2 1 2 1 2 本题主要考查如何利用简单方法求坐标系中图形的面积． 已知三角形三个顶点坐标，求三角形面积通常有三种方法： 方法一：直接法，计算三角形一边的长，并求出该边上的高； 方法二：补形法，将三角形面积转化成若干个特殊的四边形和 三角形的面积的和与差； 方法三：分割法，选择一条恰当的直线，将三角形分割成两个 便于计算面积的三角形． 建立坐标系求图形中点的坐标 【问题】正方形ABCD的边长为4，请建立一个平面直 角坐标系，并写出正方形的四个顶点A,B,C,D在这个平 面直角坐标系中的坐标. A B CD 2 4 4 y x （A） B CD 解：如图，以顶点A为原点， AB所在直线为x轴，AD所在直 线为y轴建立平面直角坐标系． 此时，正方形四个顶点A,B,C,D 的坐标分别为： A(0，0), B(4，0), C(4，4), D(0，4). O A B CD A(0，-4), B(4，-4),C(4，0), D(0，0). y xO 【想一想】还可以建立其他平 面直角坐标系，表示正方形的 四个顶点A,B,C,D的坐标吗？ A(-4，0), B(0，0),C(0，4), D(-4，4). A(-4，-4), B(0，-4),C(0，0), D(-4，0). A(-2，-2), B(2，-2),C(2，2), D(-2，2). 【追问】由上得知，建立的平面直角坐标系不同， 则各点的坐标也不同．你认为怎样建立直角坐标系 才比较适当？ 总结：平面直角坐标系建立得适当，可以容易确定图 形上的点，例如以正方形的两条边所在的直线为坐标 轴，建立平面直角坐标系．又如以正方形的中心为原 点建立平面直角坐标系．建立不同的平面直角坐标系， 同一个点就会有不同的坐标，但正方形的形状和性质 不会改变． 【例3】长方形的两条边长分别为4，6，建立适当的 直角坐标系，使它的一个顶点的坐标为(－2，－ 3)．请你写出另外三个顶点的坐标． 解：如图建立直角坐标系， ∵长方形的一个顶点的坐标为A(-2，-3)， ∴长方形的另外三个顶点的坐标分别为 B(2，－3)，C(2，3)，D(－2，3)． 由已知条件正确确定坐标轴的位置是解决本题的 关键，当建立的直角坐标系不同，其点的坐标也就不 同，但要注意，一旦直角坐标系确定以后，点的坐标 也就确定了． 【问题】 右图是一个围棋棋盘(局部)，把这个围 棋棋盘放置在一个平面直角坐标系中，白棋①的 坐标是(－2，－1)，白棋③的坐标是(－1，－3)， 则黑棋❷的坐标是________． 解析：由已知白棋①的坐标是(－2，－1)，白 棋③的坐标是(－1，－3)，可知y轴应在从左往 右数的第四条格线上，且向上为正方向，x轴 在从上往下数第二条格线上，且向右为正方向， 这两条直线的交点为坐标原点，由此可得黑棋 ②的坐标是(1，－2)． (1，－2) 1 2 3 4 1 O 3 2 –2 –1 –1 –2 –3 –4 –3-4 yA B C x 【例4】对于边长为4的正三角形△ABC，建立适当 的直角坐标系，写出各个顶点的坐标. 解:A(0,2 ), B(-2,0) ,C(2,0).3 【练一练】在一次“寻宝”游戏中，寻宝人已经找到了 坐标为（3，2）和（3，-2）的两个标志点，并且知道 藏宝地点的坐标为（4，4），如何确定直角坐标系找到 “宝藏”？ · 1 2 3 4 5-4 -3 -2 -1 3 1 4 2 5 -2 -1 -3 y ·O （3，-2） x （3，2）· ·（4，4） 解：如图所示 x y A B C １．已知A(1,4), B(-4,0),C(2,0). △ABC的面积是＿＿＿． 2.若BC的坐标不变, △ABC的面积为6,点A 的横坐标为-1,那么 点A的坐标为 ． 12 O (1,4) (-4,0) (2,0) C x y A B(-4,0) (2,0) (-1,2)或(-1,-2) O 3. 在平面直角坐标系xOy中，已知点P（2，2），点 Q在y轴上，△PQO是等腰三角形，则满足条件的点 Q共有( ) A．5个 B．4个 C．3个 D．2个 【解析】如图所示，当以OP为腰时， 分别以O、P为圆心OP为半径画弧，与y轴 有三个交点Q2，Q4，Q3，当以OP为底时， OP的垂直平分线与y轴有一个交点Q1. B 4.写出平行四边形ABCD各个顶点的坐标. A CB D O-1-2-3-4 54321 6 1 2 3 4 -1 -2 (-3,3) (-5,-2) (4,-2) (6,3) -5-6 x y A B C D E 5.下图是某植物园的平面示意图，A是大门，B、C、 D、E分别表示梅、兰、菊、竹四个花圃. 请建立平面直角坐标系，写出各花圃的坐标. hm hm 解：以A点为原点，以水平方向 为坐标轴建立直角坐标系，则 B（2，3），C（5，10）， D（8，8），E（11，9）. 建立直角坐 标系 坐标的特征 建立适当的 直角坐标系