人教版八年级数学上册第十四章整式的乘法与因式分解平方差公式教学课件 24页

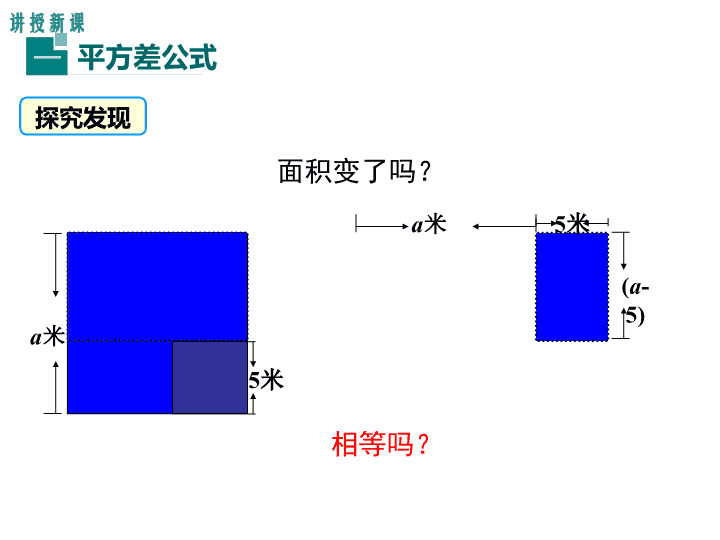
第十四章 整式的乘法与因式分解 人教版 八年级数学上册 14.2.1 平方差公式 导入新课 复习引入 多项式与多项式是如何相乘的？ （x ＋ 3)( x＋5） =x2＋5x ＋3x ＋15 =x2 ＋8x ＋15. (a+b)(m+n) =am +an +bm +bn 讲授新课 平方差公式一 探究发现 面积变了吗？ a米 5米 5米a米 (a-5) 相等吗？ ①（x ＋ 1)( x－1）； ②（m ＋ 2)( m－2）； ③（2m＋ 1)(2m－1）； ④（5y ＋ z)(5y－z）. 计算下列多项式的积，你能发现什么规律？ 算一算：看谁算得又快又准. ②（m＋ 2)( m－2）=m2 －22 ③（2m＋ 1)( 2m－1)=4m2 － 12 ④（5y ＋ z)(5y－z)= 25y2 － z2 ①（x ＋1)( x－1）=x2 － 1， 想一想：这些计算结果有什么特点？ x2 － 12 m2－22 (2m)2 － 12 (5y)2 － z2 两数和与这两数差的积,等于这两数的平方差. u公式变形: 1.（a – b ) ( a + b) = a2 - b2 2.（b + a )( -b + a ) = a2 - b2 知识要点 平方差公式 平方差公式 (a+b)(a-b)=(a)2-(b)2 相同为a 相反为b，-b 适当交换 合理加括号 (1+x)(1-x) (-3+a)(-3-a) (0.3x-1)(1+0.3x) (1+a)(-1+a) a b a2-b2 1 x -3 a 12-x2 (-3)2-a2 a 1 a2-12 0.3x 1 ( 0.3x)2-12 a2-b2 a2-b2 b2-a2 b2-a2 典例精析 例1 计算：(1) (3x＋2 )( 3x－2 ) ； (2)（-x+2y)(-x-2y). (2) 原式＝ (-x)2 - (2y)2 ＝x2 - 4y2. 解：（1）原式=(3x)2－22 =9x2－4； 方法总结：应用平方差公式计算时，应注意以下几 个问题：(1)左边是两个二项式相乘，并且这两个二 项式中有一项完全相同，另一项互为相反数；(2)右 边是相同项的平方减去相反项的平方；(3)公式中的a 和b可以是具体数，也可以是单项式或多项式． 利用平方差公式计算： (1)(3x－5)(3x＋5)； (2)(－2a－b)(b－2a)； (3)(－7m＋8n)(－8n－7m)． 针对训练 解：(1)原式=(3x)2－52＝9x2－25； (2)原式=(－2a)2－b2＝4a2－b2； (3)原式=(－7m)2－(8n)2＝49m2－64n2； 例2 计算: (1) 102×98; (2) (y+2) (y-2) – (y-1) (y+5) . 解: (1) 102×98 （2）(y+2)(y-2)- (y-1)(y+5) = 1002-22 =10000 – 4 =（100＋2）(100－2) =9996； = y2-22-(y2+4y-5) = y2-4-y2-4y+5 = - 4y + 1. 通过合理变形，利 用平方差公式，可 以简化运算. 不符合平方差公式运 算条件的乘法，按乘 法法则进行运算. 针对训练 计算: (1) 51×49; (2)(3x+4)(3x-4)-(2x+3)(3x-2) . 解: (1) 原式=（50＋1）(50－1) = 502-12 =2500 – 1 =2499； (2) 原式=(3x)2-42-(6x2+5x-6) = 9x2-16-6x2-5x+6 = 3x2-5x-10. 例3 先化简，再求值：(2x－y)(y＋2x)－(2y＋x)(2y －x)，其中x＝1，y＝2. 原式＝5×12－5×22＝－15. 解：原式＝4x2－y2－(4y2－x2) ＝4x2－y2－4y2＋x2 ＝5x2－5y2. 当x＝1，y＝2时， 例4 对于任意的正整数n，整式(3n＋1)(3n－1)－ (3－n)(3＋n)的值一定是10的整数倍吗？ 即(3n＋1)(3n－1)－(3－n)(3＋n)的值是10的倍数． 解：原式＝9n2－1－(9－n2) ＝10n2－10. ∵(10n2－10)÷10=n2-1. n为正整数， ∴n2-1为整数 方法总结：对于平方差中的a和b可以是具体的数， 也可以是单项式或多项式，在探究整除性或倍数 问题时，一般先将代数式化为最简，然后根据结 果的特征，判断其是否具有整除性或倍数关系． 例5 王大伯家把一块边长为a米的正方形土地租给 了邻居李大妈．今年王大伯对李大妈说：“我把 这块地一边减少4米，另外一边增加4米，继续租 给你，你看如何？”李大妈一听，就答应了．你 认为李大妈吃亏了吗？为什么？ ∵a2＞a2－16， 解：李大妈吃亏了． 理由：原正方形的面积为a2， 改变边长后面积为(a＋4)(a－4)＝a2－16， ∴李大妈吃亏了． 方法总结：解决实际问题的关键是根据题意列出 算式，然后根据公式化简算式，解决问题． 1.下列运算中，可用平方差公式计算的是(　　) A．(x＋y)(x＋y) B．(－x＋y)(x－y) C．(－x－y)(y－x) D．(x＋y)(－x－y) 当堂练习 C 2.计算（2x+1）（2x-1）等于（　　） A．4x2-1 B．2x2-1 C．4x-1 D．4x2+1 A 3.两个正方形的边长之和为5，边长之差为2，那 么用较大的正方形的面积减去较小的正方形的面 积，差是________．10 （1）(a+3b)(a- 3b)； =4a2－9； =4x4－y2. 原式=(2a+3)(2a-3) =a2－9b2 ； =(2a)2－32 原式=(-2x2 )2－y2 原式=(a)2－(3b)2 （2）(3+2a)(－3+2a)； （3）(－2x2－y)(－2x2+y). 4.利用平方差公式计算： 5.计算： 20152 － 2014×2016. 解： 20152 － 2014×2016 = 20152 － (2015－1)(2015+1) = 20152－ （20152－12 ) = 20152 － 20152+12 =1 （1）（a-2)(a+2)(a2 + 4) 解:原式=(a2-4)(a2+4) =a4-16. (2) (x-y)(x+y)(x2+y2)(x4+y4). 解：原式=（x2-y2)(x2+y2)(x4+y4) =（x4-y4)(x4+y4) =x8-y8. 7.先化简，再求值：(x＋1)(x－1)＋x2(1－x)＋x3， 其中x＝2. 解：原式=x2－1＋x2－x3＋x3 =2x2－1. 将x＝2代入上式， 原式=2×22-1=7.