八年级下数学课件《平行四边形》 (5)_苏科版 14页

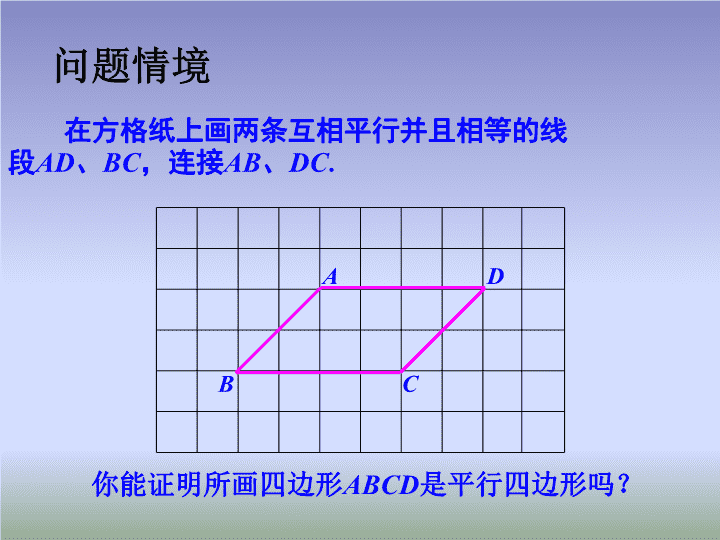
9.3　 平行四边形（2） 1.探索并掌握平行四边形的判定条件； 2.能利用平行四边形的判定方法解决有关问题． 重点与难点： 利用平行四边形的判定方法解决有关问题． 在方格纸上画两条互相平行并且相等的线 段AD、BC，连接AB、DC. 问题情境 你能证明所画四边形ABCD是平行四边形吗？ A D B C 已知：如图，在四边形ABCD中，AD//BC，AD＝ BC. 求证：四边形ABCD是平行四边形. B 　 A D C 证明：连接AC. ∵AD∥BC， ∴∠BCA=∠DAC. 在ΔBCA和ΔDAC中， CB=AD， ∠BCA=∠DAC， CA=AC， ∴ ΔBCA≌ ΔDAC ∴ ∠BAC= ∠DCA. ∴ AB∥CD. ∴四边形ABCD是平行四边形（两组对边分别平行的 四边形是平行四边形）. 定理：一组对边平行且相等的四边形是平行四边形． 几何语言： ∵AD//BC，AD＝BC， ∴四边形ABCD是平行四边形． B 　 A D C 1.一组对边平行，另一组对边相等的四边形是平行 四边形吗？ A CB E D 2.如图，AC∥ED，点B在AC上，且AB=ED=BC 。 找出图中的平行四边形. 练一练 不一定是. 比如等腰梯形 四边形ABDE、BCDE为平行四边形 探索活动 在四边形ABCD中，AB＝CD，AD＝BC.四边形ABCD是平行四 边形吗？证明你的结论. B 　 A D C 证明： 连结AC 在△ABC和△CDA中 AB=CD（已知） AD=CB （已知） AC=CA （公共边） ∴△ABC≌ △CDA（SSS） ∴∠1=∠2，∠3=∠4（全等三角形的对应角相等） ∴ AB∥CD，AD∥BC （内错角相等，两直线平行） ∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平 行四边形) 定理：两组对边分别相等的四边形是平行四边形． 几何语言： ∵AB＝DC，AD＝BC， ∴四边形ABCD是平行四边形． B 　 A D C 3.两组对边分别相等的四边形是平行四边形. 1.两组对边分别平行的四边形是平行四边形. 2. 一组对边平行且相等的四边形是平行四边形. 1. 对于四边形ABCD，如果从条件①AB∥CD ②AD∥BC③AB=CD④BC=AD中选出2个, 那么能说明四边形ABCD是平行四边形的有 _______（填序号，填出符合条件的一种情 况即可） B 　 A D C 练一练 2.判断 (1)一组对边平行且另一组对边相等的四边形是 平行四边形; ( ) (2)两组对角都相等的四边形是平行四边形 ( ) (3)一组对边平行且一组对角相等的四边形是平行 边形; ( ) (4)一组对边平行,一组邻角互补的四边形是平行 四边形; ( ) (5)两组邻角互补的四边形是平行四边形. ( ) × √ √ × × 练一练 新知应用 已知：如图，在□ABCD中，点E、F分别在AD、BC上， 且AE＝CF. 求证：四边形BFDE是平行四边形. 证明：∵四边形ABCD是平行四边形， ∴AD=BC，AD∥BC（平行四边形的 对边平行且相等）. ∵AE=CF， ∴AD-AE=BC-CF， 即 DE=BF. ∴四边形BFDE是平行四边形（一组对边平行且相等 的四边形是平行四边形）. 拓展延伸 如图，在□ABCD中，AE⊥BD，CF⊥BD，垂足分 别是E、F，求证：四边形AECF是平行四边形. F A D CB E 如图，在□ABCD中，点E、F分别在AD、BC 上，且AE=CF，AE、BE相交于点G，CE、DF 相交于点H. 求证：EF与GH互相平分。