八年级数学上册第十四章整式的乘法与因式分解14-3因式分解14-3-2第1课时运用平方差公式因式分解教学课件新版 人教版 22页

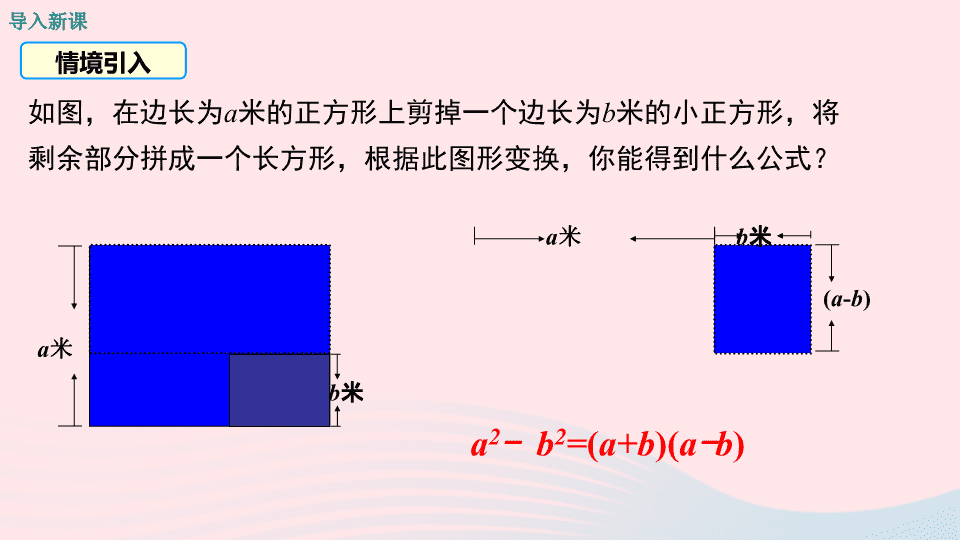
14.3.2 公式法 第十四章 整式的乘法与因式分解 第 1 课时 运用平方差公式因式分解 学习目标 1. 探索并运用平方差公式进行因式分解，体会转化思想 ．（重点） 2. 能 会综合运用提公因式法和平方差公式对多项式进行因式分解． （难点） 导入新课 a 米 b 米 b 米 a 米 ( a - b ) 情境引入 如图，在边长为 a 米的正方形上剪掉一个边长为 b 米的小正方形，将剩余部分拼成一个长方形，根据此图形变换，你能得到什么公式？ a 2 - b 2 = ( a+b )( a - b ) 讲授新课 用平方差公式进行因式分解 一 想一想： 多项式 a 2 - b 2 有什么特点？你能将它分解因式吗？ 是 a,b 两数的平方差的形式 ) )( ( b a b a - + = 2 2 b a - ) )( ( 2 2 b a b a b a - + = - 整式乘法 因式分解 两个数的 平方差 ，等于这两个数的 和 与这两个数的 差 的 乘积 . 平方差公式： √ √ × × 辨一辨： 下列多项式能否用平方差公式来分解因式，为什么？ √ √ ★ 符合平方差的形式的多项式才能用平方差公式进行因式分解，即能写成 : ( ) 2 -( ) 2 的形式 . 两数是平方， 减号在中央． （ 1 ） x 2 + y 2 （ 2 ） x 2 - y 2 （ 3 ） - x 2 - y 2 -( x 2 + y 2 ) y 2 - x 2 （ 4 ） - x 2 + y 2 （ 5 ） x 2 -25 y 2 ( x +5 y )( x -5 y ) （ 6 ） m 2 -1 ( m +1)( m -1) 例 1 分解因式： a a b b ( + ) ( - ) a 2 - b 2 = 解 :(1) 原式 = 2 x 3 2 x 2 x 3 3 (2) 原式 = [ ( x +p)+(x+q) ] [( x+p)-(x+q) ] a b 典例精析 方法总结： 公式中的 a 、 b 无论表示 数、单项式、 还是 多项式 ，只要被分解的多项式能 转化 成 平方差 的形式，就能用平方差公式因式分解 . 分解因式： (1)( a ＋ b ) 2 － 4 a 2 ； (2)9( m ＋ n ) 2 － ( m － n ) 2 . 针对训练 ＝ (4 m ＋ 2 n )(2 m ＋ 4 n ) 解： (1) 原式＝ ( a ＋ b ＋ 2 a )( a ＋ b － 2 a ) ＝ (3 a ＋ b ) ( b － a ) ； (2) 原式＝ (3 m ＋ 3 n ＋ m － n )(3 m ＋ 3 n － m ＋ n ) ＝ 4(2 m ＋ n )( m ＋ 2 n ) 若用平方差公式分解后的结果中有公因式，一定要再用提公因式法继续分解 . 当场编题，考考你！ ) )( ( 2 2 b a b a b a - + = - 20 15 2 － 20 14 2 = （ 2mn ） 2 - ( 3xy) 2 = ( x + z ) 2 - ( y + p ) 2 = 例 2 分解因式： 解： (1) 原式＝ ( x 2 ) 2 - ( y 2 ) 2 ＝ ( x 2 +y 2 )( x 2 - y 2 ) 分解因式后，一定要检查是否还有能继续分解的因式，若有，则需继续分解 . ＝ ( x 2 +y 2 )( x+y )( x - y ); (2) 原式＝ ab ( a 2 - 1) 分解因式时，一般先用提公因式法进行分解，然后再用公式法 . 最后进行检查 . ＝ ab ( a+ 1)( a - 1). 方法总结： 分解因式前应先分析多项式的特点，一般先提公因式，再套用公式．注意分解因式必须进行到每一个多项式都不能再分解因式为止． 分解因式： (1) 5 m 2 a 4 －5 m 2 b 4 ； (2) a 2 －4 b 2 － a －2 b . 针对训练 ＝ ( a ＋ 2b )( a － 2b － 1 ). ＝ 5m 2 ( a 2 ＋ b 2 )( a ＋ b )( a － b ) ； 解： (1) 原式＝ 5m 2 ( a 4 － b 4 ) ＝ 5m 2 ( a 2 ＋ b 2 ) ( a 2 － b 2 ) (2) 原式＝ ( a 2 － 4b 2 ) － ( a ＋ 2b ) ＝ ( a ＋ 2b )( a － 2b ) － ( a ＋ 2b ) 例 3 已知 x 2 － y 2 ＝－ 2 ， x ＋ y ＝ 1 ，求 x - y ， x ， y 的值． ∴ x － y ＝－ 2②. 解： ∵ x 2 － y 2 ＝ ( x ＋ y )( x － y ) ＝－ 2 ， x ＋ y ＝ 1① ， 联立 ① ② 组成二元一次方程组， 解得 方法总结： 在与 x 2 － y 2 ， x ± y 有关的求代数式或未知数的值的问题中，通常需先因式分解，然后 整体代入 或 联立方程组 求值 . 例 4 计算下列各题： (1)101 2 － 99 2 ； (2)53.5 2 × 4-46.5 2 × 4. 解： (1) 原式＝ (101 ＋ 99)(101 － 99) ＝ 400 ； (2) 原式＝ 4 (53.5 2 － 46.5 2 ) =4( 53.5 ＋ 46.5 )( 53.5 － 46.5 ) ＝ 4 × 100 × 7=2800. 方法总结： 较为复杂的有理数运算，可以运用因式分解对其进行变形，使运算得以简化 . 例 5 求证：当 n 为整数时，多项式 ( 2 n +1 ) 2 - ( 2 n -1 ) 2 一定能被8整除． 即多项式 ( 2 n +1 ) 2 - ( 2 n -1 ) 2 一定能被8整除． 证明：原式= ( 2 n +1+2 n -1 )( 2 n +1-2 n +1 ) =4 n •2=8 n ， ∵ n 为整数， ∴8 n 被8整除， 方法总结： 解决整除的基本思路就是将代数式化为整式乘积的形式，然后分析能被哪些数或式子整除． 1. 下列多项式中能用平方差公式分解因式的是 ( 　　 ) A ． a 2 ＋ ( － b ) 2 B ． 5 m 2 － 20 mn C ．－ x 2 － y 2 D ．－ x 2 ＋ 9 当堂练习 D 2. 分解因式 ( 2 x +3 ) 2 - x 2 的结果是（　　） A．3 ( x 2 +4 x +3 ) B．3 ( x 2 +2 x +3 ) C． ( 3 x +3 ) ( x +3 ) D．3 ( x +1 )( x +3 ) D 3. 若 a + b =3 ， a - b =7 ，则 b 2 - a 2 的值为（　　） A ． -21 B ． 21 C ． -10 D ． 10 A 4. 把下列各式分解因式： (1) 16 a 2 -9 b 2 =_________________; (2) ( a + b ) 2 -( a - b ) 2 =_________________; (3) 9 xy 3 -36 x 3 y =_________________; (4) - a 4 +16 =_________________. (4 a +3 b )(4 a -3 b ) 4 ab 9 xy ( y +2 x )( y -2 x ) (4+ a 2 )(2+ a )(2- a ) 5. 若将 ( 2 x ) n -81分解成 ( 4 x 2 +9 )( 2 x +3 )( 2 x -3 ) ，则 n 的值是 _____________. 4 6. 已知4 m + n =40，2 m - 3 n =5．求 ( m +2 n ) 2 - ( 3 m - n ) 2 的值． 原式= - 40×5= - 200． 解：原式= ( m +2 n +3 m - n )( m +2 n - 3m+ n ) = ( 4 m +n )( 3 n - 2 m ) = - ( 4 m + n ) （2 m - 3 n ) ， 当4 m + n =40，2 m - 3 n =5时， 7. 如图，在边长为 6.8 cm 正方形钢板上，挖去 4 个边长为 1.6 cm 的小正方形，求剩余部分的面积． 解：根据题意，得 6.8 2 －4×1.6 2 ＝ 6.8 2 － (2×1.6) 2 ＝ 6.8 2 －3.2 2 ＝ (6.8 ＋ 3.2)(6.8 － 3.2) ＝ 10×3.6 ＝ 36 (cm 2 ) 答：剩余部分的面积为 36 cm 2 . 8. (1)99 2 -1 能否被 100 整除吗？ 解： (1) 因为 99 2 -1=(99+1)(99-1)=100×98 ， 所以， (2 n +1) 2 -25 能被 4 整除 . (2) n 为整数 , （ 2 n +1) 2 -25 能否被 4 整除？ 所以 99 2 -1 能否被 100 整除 . (2) 原式 = ( 2 n +1+5 ) (2 n +1-5) =(2 n +6)(2 n -4) =2( n +3) ×2( n -2)=4( n +3)( n -2). 课堂小结 平方差公式分解因式 公式 a 2 - b 2 =( a+b )( a-b ) 步骤 一提：公因式； 二套：公式； 三查：多项式的因式分解有没有分解到不能再分解为止 .