数学华东师大版八年级上册课件13-5 逆命题与逆定理 第3课时 18页

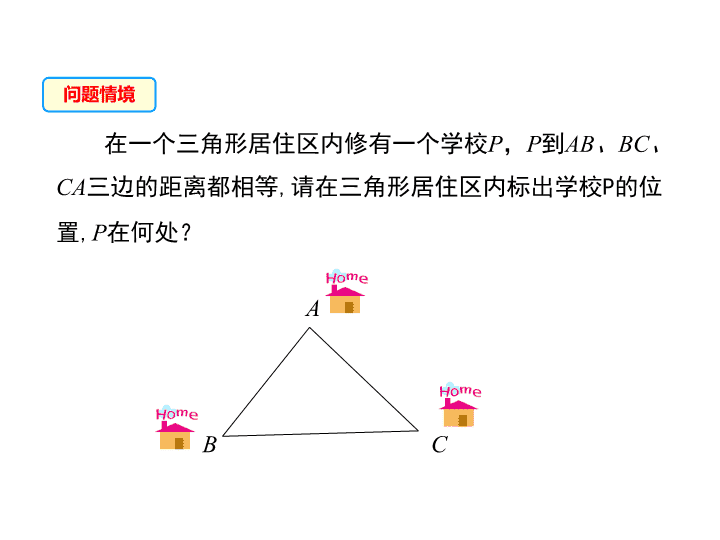
第13章 全等三角形 13.5 逆命题与逆定理 第3课时 1.会叙述角平分线的性质及判定；（重点） 2.能利用三角形全等，证明角平分线的性质定理，理解和 掌握角平分线性质定理和它的逆定理．能应用这两个性 质解决一些简单的实际问题；（难点） 3.经历探索、猜想、证明的过程，进一步发展学生的推理 证明意识和能力． 学习目标 在一个三角形居住区内修有一个学校P，P到AB、BC、 CA三边的距离都相等,请在三角形居住区内标出学校P的位 置,P在何处？ A B C 问题情境 角平分线的性质定理一 如图，点P是∠AOB的角平分线OC上的任意一点，且 PD⊥OA于点D，PE⊥OB于点E，将∠AOB沿OC对折，你 发现了什么？如何表达，并简述你的证明过程. 对折后PD、PE能够完全重合，PD=PE. 角是轴对称图形吗？它的对称轴是什么？ D P A C BEO 证明:∵ OC平分∠AOB, P是OC上一点， ∴∠DOP=∠BOP. ∵PD⊥OA,PE⊥OB ， ∴∠ODP=∠OEP=90°. 在△OPD和△OPE 中， ∠DOP=∠EOP ,∠ODP=∠OEP ,OP=OP, ∴ △OPD≌△OPE (A.A.S.). ∴PD＝PE（全等三角形的对应边相等）. 下面我们来证明刚才得到的结论. D P A C BEO 已知:OC平分∠AOB，P是OC上任意一点，PD⊥OA， PE⊥OB .求证:PD=PE. 由上面证明，我们得到角平分线的性质定理: 角平分线上的点到角两边的距离相等． 几何语言描述：∵ OC平分∠AOB， 且PD⊥OA， PE⊥OB. ∴ PD= PE. 应用所具备的条件： （1）角的平分线； （2）点在该平分线上； （3）垂直距离. 定理的作用： 证明线段相等. 这一定理描述了角平分线的性质，那么反过来会有什 么结果呢？ 写出性质定理及其逆命题的条件和结论，你有什么发现？ t条 件 结 论 性质定理 逆命题 一个点在角的平 分线上 这个点到这个角 两边的距离相等 一个点到角两边 的距离相等 这个点在这个角 的平分线上 想想看，这个逆命题是否是一个真命题？你能证明吗？ 角平分线性质定理的逆定理二 逆命题 如果一个点到角两边的距离相等，那么这 个点在这个角的平分线上. 分析：为了证明点P在∠AOB 的平分线上，可以先作射线OP， 然后证明Rt△PDO≌Rt△PEO， 从而得到∠AOP=∠BOP. 已知：如图，PD⊥OA，PE⊥OB，垂足分别是D、E，PD=PE. 求证：点P在∠AOB的角平分线上. B AD O P E 证明： 作射线OP， 在Rt△PDO和Rt△PEO 中， （全等三角形的对应角相等）. OP=OP（公共边）， PD= PE（已知）， ∵PD⊥OA,PE⊥OB， ∴∠PDO=∠PEO=90°， ∴Rt△PDO≌Rt△PEO（ H.L.）. ∴∠AOP=∠BOP B AD O P E ∴点P在∠AOB的平分线上. 判定定理： 角的内部到角两边距离相等的点在角的平分线上. 应用所具备的条件： （1）位置关系：点在角的内部； （2）数量关系：该点到角两边距离相等. 定理的作用：判断点在角平分线上. 应用格式： ∵ PD⊥OA,PE⊥OB，PD=PE， ∴点P 在∠AOB的平分线上. D P A C BEO 角平分线的判定定理与性质定理互为逆定理. 利用尺规作三角形的三条角平分线，你发现了什么？ 发现：三角形的三条角平分线交于一点． 做一做 怎样证明这个结论呢? A B C P N M 点拨：要证明三角形的三条角平分线 相交于一点，只要证明其中两条角平 分线的交点一定在第三条角平分线上 即可.思路可表示如下： 试试看，你会写出证明过程吗？ AP是∠BAC 的平分线 BP是∠ABC 的平分线   PI=PH PG=PI PH=PG  点P在∠BCA 的平分线上 A B C P F H D E I G A B C P 例 如图，△ABC的角平分线BM，CN相交于点P. 求证：点P也在∠A的平分线上. N M 典例精析 证明：过点P作PD⊥AB，PE⊥BC， PF⊥AC, 垂足分别为D、E、F. ∵BM是△ABC的角平分线，点P在BM上（已知）, ∴PD=PE（角平分线上的点到角两边的距离相等）. 同理 PE=PF. ∴ PD=PF（等量代换）. ∴ 点P在∠A的平分线上, 即点P到AB、BC、CA三边的 距离相等. A B C P E D F M N 当堂练习 1.如图， DE⊥AB， DF⊥BC， 垂足分别是E， F， DE =DF，∠EDB= 60°， 则 ∠EBF= ，BE= ．60° BF A B C D E F 2.如图，△ABC中，∠C=90°，DE⊥AB， ∠CBE=∠ABE，且AC=6cm，那么线段BE是 ∠ABC的　 ，AE+DE= . C A B E D 角平分线 6cm 　3.已知：如图，△ABC中，∠C=90°，AD是△ABC的角平 分线，DE⊥AB于E，F在AC上,BD=DF. 　求证：CF=EB. 证明：∵AD平分∠CAB, 　　DE⊥AB，∠C＝90°（已知）, ∴　CD＝DE (角平分线的性质). 在Rt△CDF和Rt△EDB中, 　　 CD=ED（已证）, DF=DB （已知）, ∴ Rt△CDF≌Rt△EDB (H.L.). ∴ CF=EB（全等三角形的对应边相等）. C F A E D B 角平分线 的性质及 判定 性质定理：角平分线上的点 到角两边的距离相等. 判定定理：角的内部到角两 边距离相等的点在角的平分 线上. 课堂小结