八年级上册青岛版数学教案2-6等腰三角形（第1课时） 3页

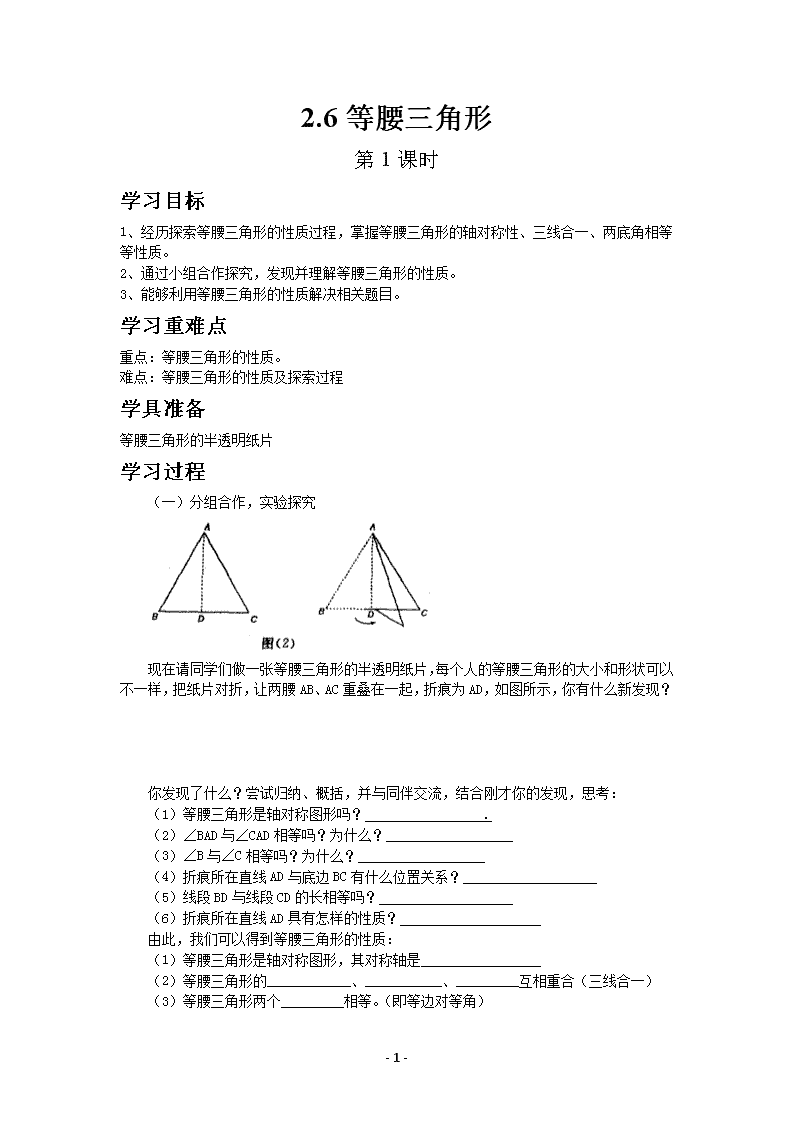
- 1 - 2.6 等腰三角形 第 1 课时 学习目标 1、经历探索等腰三角形的性质过程，掌握等腰三角形的轴对称性、三线合一、两底角相等 等性质。 2、通过小组合作探究，发现并理解等腰三角形的性质。 3、能够利用等腰三角形的性质解决相关题目。 学习重难点 重点：等腰三角形的性质。 难点：等腰三角形的性质及探索过程 学具准备 等腰三角形的半透明纸片 学习过程 （一）分组合作，实验探究 现在请同学们做一张等腰三角形的半透明纸片，每个人的等腰三角形的大小和形状可以 不一样，把纸片对折，让两腰 AB、AC 重叠在一起，折痕为 AD，如图所示，你有什么新发现？ 你发现了什么？尝试归纳、概括，并与同伴交流，结合刚才你的发现，思考： （1）等腰三角形是轴对称图形吗？ . （2）∠BAD 与∠CAD 相等吗？为什么？ （3）∠B 与∠C 相等吗？为什么？ （4）折痕所在直线 AD 与底边 BC 有什么位置关系？ （5）线段 BD 与线段 CD 的长相等吗？ （6）折痕所在直线 AD 具有怎样的性质？ 由此，我们可以得到等腰三角形的性质： （1）等腰三角形是轴对称图形，其对称轴是 （2）等腰三角形的____________、___________、_________互相重合（三线合一） （3）等腰三角形两个_________相等。（即等边对等角） - 2 - h a （二）知识应用 （1）在△ABC 中，AB=AC，D 在 BC 上， 如果 AD⊥BC，那么∠BAD=∠ ，BD= 如果∠BAD=∠CAD，那么 AD⊥ ，BD= 如果 BD=CD，那么∠BAD=∠ ，AD⊥ （2）已知一个等腰三角形一腰上的高与另一腰的夹角是 40°，求顶角的度数。 （三）例题探究 如图所示，屋椽 AB 和 AC 的长相等，∠A=120 度，求∠B 的度数。 自主解决： （四）分组合作，实验探究 根据等腰三角形的性质作图： 已知底边及底边上的高作等腰三角形。 已知：底边 a、及底边上的高 h。（画出两条线段 a、h） 求作：△ABC，使得一底边为 a、底边上的高为 h。 小组交流： 问题 1：要完成这个作图，先作出 ， 再 ，最后 。 问题 2：为什么这样画出的三角形是等腰三角形？ 请你写出作法，并独立完成作图。 （五）反思提高 通过这节课的学习，你有哪些收获？ （六）课堂测试 1、若等腰三角形的顶角为 80°，则它的底角度数为（ ） A．80° B．50° C．40° D．20° 2、一个等腰三角形两边的长分别为 4 和 9，那么这个三角形的周长是（ ） A．13 B．17 C．22 D．17 或 22 3、 如图，在△ABC 中，AB=AC，∠A=40°，BD 为∠ABC 的平分线，则∠BDC= - 3 - 4、 如图所示，已知等腰三角形 ABC，AB 边的垂直平分线交 AC 于 D，AB=AC=8，BC=6，求 △BDC 周长． 参考答案： 1、B 2、C 3、75° 4、解：由等腰三角形的性质及题意得 △BDC 周长=BC+CD+BD= BC+CD+AD= BC+AC=14