- 248.35 KB
- 2021-10-27 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
14.3 实数
导入新课 讲授新课 当堂练习 课堂小结
第1课时 无理数及实数的概念
1.理解无理数的概念.(难点)
2.理解实数的概念.(重点)
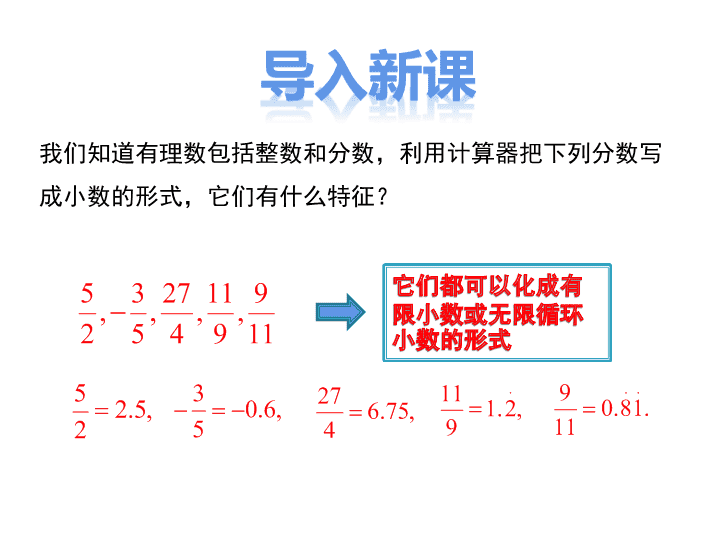
我们知道有理数包括整数和分数,利用计算器把下列分数写
成小数的形式,它们有什么特征?
5 3 27 11 9, , , ,2 5 4 9 11
5 2.5,2
3 0.6,5
27 6.75,4
.11 1.2,9
. .9 0.81.11
无理数及实数的概念
问题1 是一个有理数吗?
解:
2
∵ 12=1, 22=4,
∴ 1 < < 2.
∵ 1.42=1.96, 1.52=2.25,
∴ 1.4 < < 1.5.
∵ 1.412=1.9881, 1.422=2.0164,
∴ 1.41 < < 1.42.
∵ 1.4142=1.9881, 1.4152=2.002225,
∴ 1.414 < < 1.415.
=1.414213562373…
2
2
2
2
2
问题2 含π的一些数是无理数吗?
π 3.141 592 65...
u无理数的概念
我们把这种无限且不循环的小数叫做无理数.
不循环的无限小数都是无理数.
u无理数的常见形式
(1)含π的一些数;
(2)开不尽方的数;
(3)有规律但不循环的数,如1.010 010 001 000 01…
例 判断下列数哪些是有理数?哪些是无理数?
判断一个数是不是无理数,就看这个数是否含π、含开
不尽方的数、含有规律但不循环的数即可.
36 ,7
22 ,32.1 ,2 ,6
解:有理数:
无理数:
221.23, , 36.7
6, .2
u实数
有理数和无理数统称为实数.
想一想 无理数与实数有什么区别?
无理数与实数的区别:(1)有理数是有限循环小数或无限循
环小数,而无理数是无限不循环小数;
(2)有理数是正数或者分数,任何一个有理数都可以写成分
数的形式,无理数都不能写成整式或分数的形式.
A.不存在最小是实数
1.下列说法中正确的是 ( )
B.有理数、是有限小数
C.无限小数都是无理数
D.带根号的数都是无理数
A
2.把下列各数分别填入相应的集合内:
,4
1
,23 ,7 , ,2
5 ,2
,3
20 ,5 ,83,9
4 ,0
3737737773.0 (相邻两个3之间的7的个数逐次加1)
有理数集合 无理数集合
,83,4
1 ,2
5
,9
4 ,0
,23 ,7 , ,2 ,3
20
,5 3737737773.0
3.已知长方体的体积是1 620,它的长、宽、高的比是
5∶ 4∶ 3,问该长方体的长、宽、高是无理数吗?为什么?
解: 该长方体的长、宽、高不是无理数.理由如下:
设长方体的长、宽、高分别是5k、4k、3k.
根据题意得5k·4k·3k=1 620,k3=27,k=3.
所以5k=15,4k=12,3k=9.
所以该长方体的长、宽、高均为有理数,不是无理数.
u无理数的概念
我们把这种无限且不循环的小数叫做无理数.
不循环的无限小数都是无理数.
u无理数的常见形式
(1)含π的一些数;
(2)开不尽方的数;
(3)有规律但不循环的数,如1.010 010 001 000 01…
u实数
有理数和无理数统称为实数.
相关文档
- 2019秋人教部编版八年级语文上册教2021-10-2729页
- 部编版八年级上册-《道德与法治》2021-10-2726页
- 八年级数学上册第三章中心对称图形2021-10-2719页
- 八年级上语文课件雪 (12)_鲁教版2021-10-278页
- 八年级下册语文课件《壶口瀑布》 2021-10-2731页
- 24 大道之行也精品课件一2021-10-2733页
- 2019秋八年级数学上册第5章二次根2021-10-2719页
- 华东师大版数学八年级上册《13.2.52021-10-275页
- 八年级下数学课件课外练习_图形的2021-10-271页
- 八年级上数学课件- 11-2-2 三角形2021-10-2716页