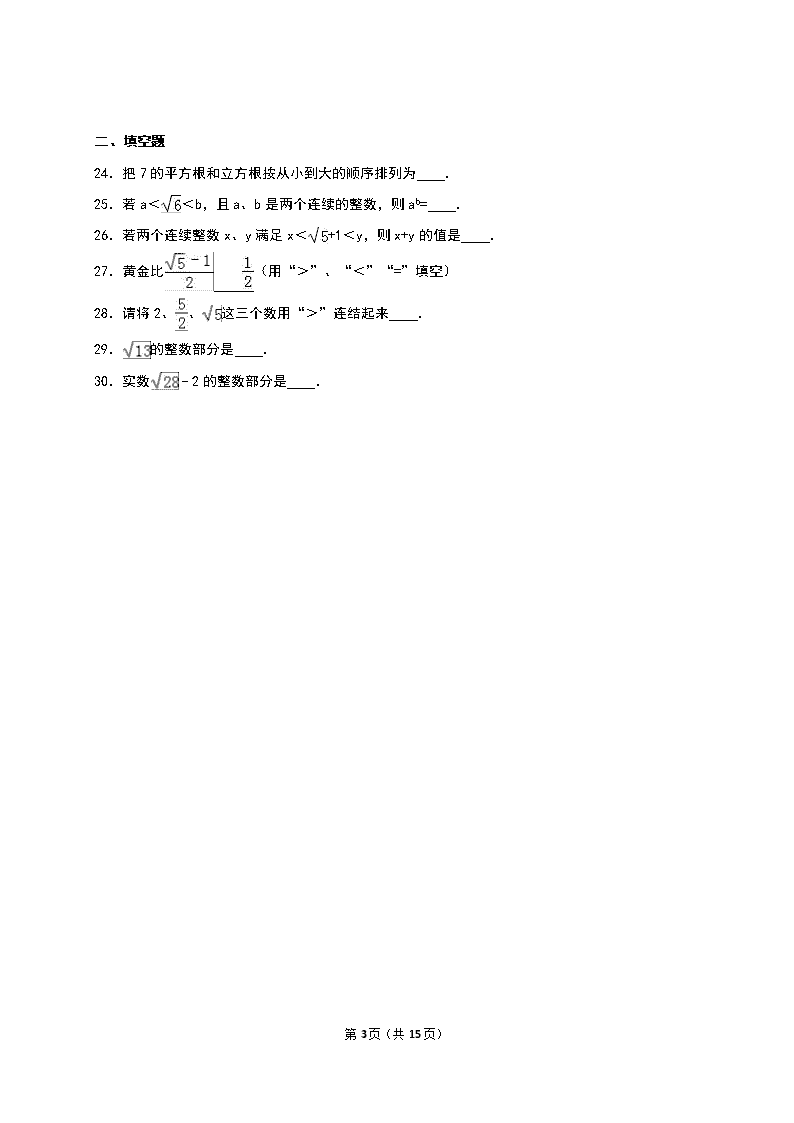华东师大版八年级上册第11章 数的开方单元试卷及答案 15页

第 1页（共 15页） 第 11 章 数的开方 一、选择题 1．在﹣3，0，4， 这四个数中，最大的数是（ ） A．﹣3 B．0 C．4 D． 2．下列实数中，最小的数是（ ） A．﹣3 B．3 C． D．0 3．在实数 1、0、﹣1、﹣2 中，最小的实数是（ ） A．﹣2 B．﹣1 C．1 D．0 4．实数 1，﹣1，﹣ ，0，四个数中，最小的数是（ ） A．0 B．1 C．﹣1 D．﹣ 5．在实数﹣2，0，2，3 中，最小的实数是（ ） A．﹣2 B．0 C．2 D．3 6．a，b 是两个连续整数，若 a＜ ＜b，则 a，b 分别是（ ） A．2，3 B．3，2 C．3，4 D．6，8 7．估算 ﹣2 的值（ ） A．在 1 到 2 之间 B．在 2 到 3 之间 C．在 3 到 4 之间 D．在 4 到 5 之间 8．在已知实数：﹣1，0， ，﹣2 中，最小的一个实数是（ ） A．﹣1 B．0 C． D．﹣2 9．下列四个实数中，绝对值最小的数是（ ） A．﹣5 B． C．1 D．4 10．在﹣2，0，3， 这四个数中，最大的数是（ ） A．﹣2 B．0 C．3 D． 11．在 1，﹣2，4， 这四个数中，比 0 小的数是（ ） A．﹣2 B．1 C． D．4 12．四个实数﹣2，0，﹣ ，1 中，最大的实数是（ ） A．﹣2 B．0 C．﹣ D．1 13．与无理数 最接近的整数是（ ） 第 2页（共 15页） A．4 B．5 C．6 D．7 14．如图，已知数轴上的点 A、B、C、D 分别表示数﹣2、1、2、3，则表示数 3﹣ 的点 P 应落在线 段（ ） A．AO 上 B．OB 上 C．BC 上 D．CD 上 15．估计 介于（ ） A．0.4 与 0.5 之间 B．0.5 与 0.6 之间 C．0.6 与 0.7 之间 D．0.7 与 0.8 之间 16．若 m= ×（﹣2），则有（ ） A．0＜m＜1 B．﹣1＜m＜0 C．﹣2＜m＜﹣1 D．﹣3＜m＜﹣2 17．如图，表示 的点在数轴上表示时，所在哪两个字母之间（ ） A．C 与 D B．A 与 B C．A 与 C D．B 与 C 18．与 1+ 最接近的整数是（ ） A．4 B．3 C．2 D．1 19．在数轴上标注了四段范围，如图，则表示 的点落在（ ） A．段① B．段② C．段③ D．段④ 20．若 a=（﹣3）13﹣（﹣3）14，b=（﹣0.6）12﹣（﹣0.6）14，c=（﹣1.5）11﹣（﹣1.5）13，则下列 有关 a、b、c 的大 小关系，何者正确？（ ） A．a＞b＞c B．a＞c＞b C．b＞c＞a D．c＞b＞a 21．若 k＜ ＜k+1（k 是整数），则 k=（ ） A．6 B．7 C．8 D．9 22．估计 × + 的运算结果应在哪两个连续自然数之间（ ） A．5 和 6 B．6 和 7 C．7 和 8 D．8 和 9 23．估计 的值在（ ） A．在 1 和 2 之间 B．在 2 和 3 之间 C．在 3 和 4 之间 D．在 4 和 5 之间 第 3页（共 15页） 二、填空题 24．把 7 的平方根和立方根按从小到大的顺序排列为 ． 25．若 a＜ ＜b，且 a、b 是两个连续的整数，则 ab= ． 26．若两个连续整数 x、y 满足 x＜ +1＜y，则 x+y 的值是 ． 27．黄金比 （用“＞”、“＜”“=”填空） 28．请将 2、 、 这三个数用“＞”连结起来 ． 29． 的整数部分是 ． 30．实数 ﹣2 的整数部分是 ． 第 4页（共 15页） 第 11 章 数的开方 参考答案与试题解析 一、选择题 1．在﹣3，0，4， 这四个数中，最大的数是（ ） A．﹣3 B．0 C．4 D． 【考点】实数大小比较． 【分析】根据有理数大小比较的法则进行判断即可． 【解答】解：在﹣3，0，4， 这四个数中，﹣3＜0＜ ＜4， 最大的数是 4． 故选 C． 【点评】本题考查了有理数大小比较的法则，解题的关键是牢记法则，正数都大于 0；负数都小于 0； 正数大于一切负数；两个负数，绝对值大的其值反而小是本题的关键． 2．下列实数中，最小的数是（ ） A．﹣3 B．3 C． D．0 【考点】实数大小比较． 【分析】在数轴上表示出各数，再根据数轴的特点即可得出结论． 【解答】解：如图所示： 故选 A． 【点评】本题考查的是实数的大小比较，利用数形结合求解是解答此题的关键． 3．在实数 1、0、﹣1、﹣2 中，最小的实数是（ ） A．﹣2 B．﹣1 C．1 D．0 【考点】实数大小比较． 【分析】先在数轴上表示出各数，再根据数轴的特点进行解答即可． 第 5页（共 15页） 【解答】解：如图所示： ∵由数轴上各点的位置可知，﹣2 在数轴的最左侧， ∴四个数中﹣2 最小． 故选 A． 【点评】本题考查的是实数的大小比较，熟知数轴上的任意两个数，右边的数总比左边的数大是解 答此题的关键． 4．实数 1，﹣1，﹣ ，0，四个数中，最小的数是（ ） A．0 B．1 C．﹣1 D．﹣ 【考点】实数大小比较． 【专题】常规题型． 【分析】根据正数＞0＞负数，几个负数比较大小时，绝对值越大的负数越小解答即可． 【解答】解：根据正数＞0＞负数，几个负数比较大小时，绝对值越大的负数越小， 可得 1＞0＞﹣ ＞﹣1， 所以在 1，﹣1，﹣ ，0 中，最小的数是﹣1． 故选：C． 【点评】此题主要考查了正、负数、0 和负数间的大小比较．几个负数比较大小时，绝对值越大的 负数越小， 5．在实数﹣2，0，2，3 中，最小的实数是（ ） A．﹣2 B．0 C．2 D．3 【考点】实数大小比较． 【专题】常规题型． 【分析】根据正数大于 0，0 大于负数，可得答案． 【解答】解：﹣2＜0＜2＜3，最小的实数是﹣2， 故选：A． 【点评】本题考查了实数比较大小，正数大于 0，0 大于负数是解题关键． 第 6页（共 15页） 6． a，b 是两个连续整数，若 a＜ ＜b，则 a，b 分别是（ ） A．2，3 B．3，2 C．3，4 D．6，8 【考点】估算无理数的大小． 【分析】根据 ，可得答案． 【解答】解：根据题意，可知 ，可得 a=2，b=3． 故选：A． 【点评】本题考查了估算无理数的大小， 是解题关键． 7．估算 ﹣2 的值（ ） A．在 1 到 2 之间 B．在 2 到 3 之间 C．在 3 到 4 之间 D．在 4 到 5 之间 【考点】估算无理数的大小． 【分析】先估计 的整数部分，然后即可判断 ﹣2 的近似值． 【解答】解：∵5＜ ＜6， ∴3＜ ﹣2＜4． 故选 C． 【点评】此题主要考查了无理数的估算能力，现实生活中经常需要估算，估算应是我们具备的数学 能力，“夹逼法”是估算的一般方法，也是常用方法． 8．在已知实数：﹣1，0， ，﹣2 中，最小的一个实数是（ ） A．﹣1 B．0 C． D．﹣2 【考点】实数大小比较． 【专题】常规题型． 【分析】正实数都大于 0，负实数都小于 0，正实数大于一切负实数，两个负实数绝对值大的反而小， 由此可得出答案． 【解答】解：﹣2、﹣1、0、1 中，最小的实数是﹣2． 故选：D． 【点评】本题考查了实数的大小比较，属于基础题，掌握实数的大小比较法则是关键． 第 7页（共 15页） 9．下列四个实数中，绝对值最小的数是（ ） A．﹣5 B． C．1 D．4 【考点】实数大小比较． 【分析】计算出各选项的绝对值，然后再比较大小即可． 【解答】解：|﹣5|=5；|﹣ |= ，|1|=1，|4|=4， 绝对值最小的是 1． 故选 C． 【点评】本题考查了实数的大小比较，属于基础题，注意先运算出各项的绝对值． 10．在﹣2，0，3， 这四个数中，最大的数是（ ） A．﹣2 B．0 C．3 D． 【考点】实数大小比较． 【专题】常规题型． 【分析】根据正数大于 0，0 大于负数，可得答案． 【解答】解：﹣2＜0＜ ＜3， 故选：C． 【点评】本题考查了实数比较大小， 是解题关键． 11．在 1，﹣2，4， 这四个数中，比 0 小的数是（ ） A．﹣2 B．1 C． D．4 【考点】实数大小比较． 【专题】常规题型． 【分析】根据有理数比较大小的法则：负数都小于 0 即可选出答案． 【解答】解：﹣2、1、4、 这四个数中比 0 小的数是﹣2， 故选：A． 【点评】此题主要考查了有理数的比较大小，关键是熟练掌握有理数大小比较的法则： ①正数都大于 0； ②负数都小于 0； ③正数大于一切负数； ④两个负数，绝对值大的其值反而小． 第 8页（共 15页） 12．四个实数﹣2，0，﹣ ，1 中，最大的实数是（ ） A．﹣2 B．0 C．﹣ D．1 【考点】实数大小比较． 【分析】根据正数大于 0，0 大于负数，正数大于负数，比较即可． 【解答】解：∵﹣2＜﹣ ＜0＜1， ∴四个实数中，最大的实数是 1． 故选：D． 【点评】本题考查了实数大小比较，关键要熟记：正实数都大于 0，负实数都小于 0，正实数大于一 切负实数，两个负实数绝对值大的反而小． 13．与无理数 最接近的整数是（ ） A．4 B．5 C．6 D．7 【考点】估算无理数的大小． 【分析】根据无理数的意义和二次根式的性质得出 ＜ ＜ ，即可求出答案． 【解答】解：∵ ＜ ＜ ， ∴ 最接近的整数是 ， =6， 故选：C． 【点评】本题考查了二次根式的性质和估计无理数的大小等知识点，主要考查学生能否知道 在 5 和 6 之间，题目比较典型． 14．如图，已知数轴上的点 A、B、C、D 分别表示数﹣2、1、2、3，则表示数 3﹣ 的点 P 应落在线 段（ ） A．AO 上 B．OB 上 C．BC 上 D．CD 上 【考点】估算无理数的大小；实数与数轴． 【分析】根据估计无理数的方法得出 0＜3﹣ ＜1，进而得出答案． 【解答】解：∵2＜ ＜3， 第 9页（共 15页） ∴0＜3﹣ ＜1， 故表示数 3﹣ 的点 P 应落在线段 OB 上． 故选：B． 【点评】此题主要考查了估算无理数的大小，得出 的取值范围是解题关键． 15．估计 介于（ ） A．0.4 与 0.5 之间 B．0.5 与 0.6 之间 C．0.6 与 0.7 之间 D．0.7 与 0.8 之间 【考点】估算无理数的大小． 【分析】先估算 的范围，再进一步估算 ，即可解答． 【解答】解：∵2.22=4.84，2.32=5.29， ∴2.2＜ ＜2.3， ∵ =0.6， =0.65， ∴0.6＜ ＜0.65． 所以 介于 0.6 与 0.7 之间． 故选：C． 【点评】本题考查了估算有理数的大小，解决本题的关键是估算 的大小． 16．若 m= ×（﹣2），则有（ ） A．0＜m＜1 B．﹣1＜m＜0 C．﹣2＜m＜﹣1 D．﹣3＜m＜﹣2 【考点】估算无理数的大小． 【分析】先把 m 化简，再估算 大小，即可解答． 【解答】解；m= ×（﹣2）= ， ∵ ， ∴ ， 故选：C． 【点评】本题考查了公式无理数的大小，解决本题的关键是估算 的大小． 第 10页（共 15页） 17．如图，表示 的点在数轴上表示时，所在哪两个字母之间（ ） A．C 与 D B．A 与 B C．A 与 C D．B 与 C 【考点】估算无理数的大小；实数与数轴． 【专题】计算题． 【分析】确定出 7 的范围，利用算术平方根求出 的范围，即可得到结果． 【解答】解：∵6.25＜7＜9， ∴2.5＜ ＜3， 则表示 的点在数轴上表示时，所在 C 和 D 两个字母之间． 故选 A 【点评】此题考查了估算无理数的大小，以及实数与数轴，解题关键是确定无理数的整数部分即可 解决问题． 18．与 1+ 最接近的整数是（ ） A．4 B．3 C．2 D．1 【考点】估算无理数的大小． 【分析】由于 4＜5＜9，由此根据算术平方根的概念可以找到 5 接近的两个完全平方数，再估算与 1+ 最接近的整数即可求解． 【解答】解：∵4＜5＜9， ∴2＜ ＜3． 又 5 和 4 比较接近， ∴ 最接近的整数是 2， ∴与 1+ 最接近的整数是 3， 故选：B． 【点评】此题主要考查了无理数的估算能力，估算无理数的时候，“夹逼法”是估算的一般方法， 也是常用方法． 19．在数轴上标注了四段范围，如图，则表示 的点落在（ ） 第 11页（共 15页） A．段① B．段② C．段③ D．段④ 【考点】估算无理数的大小；实数与数轴． 【分析】根据数的平方，即可解答． 【解答】解：2.62=6.76，2.72=7.29，2.82=7.84，2.92=8.41，32=9， ∵7.84＜8＜8.41， ∴ ， ∴ 的点落在段③， 故选：C． 【点评】本题考查了估算无理数的大小，解决本题的关键是计算出各数的平方． 20．若 a=（﹣3）13﹣（﹣3）14，b=（﹣0.6）12﹣（﹣0.6）14，c=（﹣1.5）11﹣（﹣1.5）13，则下列 有关 a、b、c 的大 小关系，何者正确？（ ） A．a＞b＞c B．a＞c＞b C．b＞c＞a D．c＞b＞a 【考点】实数大小比较． 【分析】分别判断出 a﹣b 与 c﹣b 的符号，即可得出答案． 【解答】解：∵a﹣b=（﹣3）13﹣（﹣3）14﹣（﹣0.6）12+（﹣0.6）14=﹣313﹣314﹣ 12+ 14＜0， ∴a＜b， ∵c﹣b=（﹣1.5）11﹣（﹣1.5）13﹣（﹣0.6）12+（﹣0.6）14=（﹣1.5）11+1.513﹣0.612+0.614＞0， ∴c＞b， ∴c＞b＞a． 故选 D． 【点评】此题考查了实数的大小比较，关键是通过判断两数的差，得出两数的大小． 21．若 k＜ ＜k+1（k 是整数），则 k=（ ） A．6 B．7 C．8 D．9 【考点】估算无理数的大小． 第 12页（共 15页） 【分析】根据 =9， =10，可知 9＜ ＜10，依此即可得到 k 的值． 【解答】解：∵k＜ ＜k+1（k 是整数），9＜ ＜10， ∴k=9． 故选：D． 【点评】本题考查了估算无理数的大小，解题关键是估算 的取值范围，从而解决问题． 22．估计 × + 的运算结果应在哪两个连续自然数之间（ ） A．5 和 6 B．6 和 7 C．7 和 8 D．8 和 9 【考点】估算无理数的大小；二次根式的乘除法． 【分析】先把各二次根式化为最简二次根式，再进行计算． 【解答】解： × + =2 × +3 =2+3 ， ∵6＜2+3 ＜7， ∴ × + 的运算结果在 6 和 7 两个连续自然数之间， 故选：B． 【点评】本题考查的是二次根式的混合运算，在进行此类运算时一般先把二次根式化为最简二次根 式的形式后再运算．最后估计无理数的大小． 23．估计 的值在（ ） A．在 1 和 2 之间 B．在 2 和 3 之间 C．在 3 和 4 之间 D．在 4 和 5 之间 【考点】估算无理数的大小． 【专题】计算题． 【分析】由于 9＜11＜16，于是 ＜ ＜ ，从而有 3＜ ＜4． 【解答】解：∵9＜11＜16， ∴ ＜ ＜ ， ∴3＜ ＜4． 故选 C． 【点评】本题考查了无理数的估算，解题关键是确定无理数的整数部分即可解决问题． 二、填空题 第 13页（共 15页） 24．把 7 的平方根和立方根按从小到大的顺序排列为 ． 【考点】实数大小比较． 【专题】计算题． 【分析】先分别得到 7 的平方根和立方根，然后比较大小． 【解答】解：7 的平方根为﹣ ， ；7 的立方根为 ， 所以 7 的平方根和立方根按从小到大的顺序排列为﹣ ＜ ＜ ． 故答案为：﹣ ＜ ＜ ． 【点评】本题考查了实数大小比较：正数大于 0，负数小于 0；负数的绝对值越大，这个数越小． 25．若 a＜ ＜b，且 a、b 是两个连续的整数，则 ab= 8 ． 【考点】估算无理数的大小． 【分析】先估算出 的范围，即可得出 a、b 的值，代入求出即可． 【解答】解：∵2＜ ＜3， ∴a=2，b=3， ∴ab=8． 故答案为：8． 【点评】本题考查了估算无理数的大小的应用，解此题的关键是求出 的范围． 26．若两个连续整数 x、y 满足 x＜ +1＜y，则 x+y 的值是 7 ． 【考点】估算无理数的大小． 【分析】先估算 的范围，再估算 +1，即可解答． 【解答】解：∵ ， ∴ ， ∵x＜ +1＜y， ∴x=3，y=4， ∴x+y=3+4=7． 故答案为：7． 【点评】本题考查了估算无理数的大小，解决本题的关键是估算 的范围． 第 14页（共 15页） 27．黄金比 ＞ （用“＞”、“＜”“=”填空） 【考点】实数大小比较． 【分析】根据分母相同，比较分子的大小即可，因为 2＜ ＜3，从而得出 ﹣1＞1，即可比较大 小． 【解答】解：∵2＜ ＜3， ∴1＜ ﹣1＜2， ∴ ＞ ， 故答案为：＞． 【点评】本题考查了实数的大小比较，解题的关键是熟练掌握 在哪两个整数之间，再比较大小． 28．请将 2、 、 这三个数用“＞”连结起来 ＞ ＞2 ． 【考点】实数大小比较． 【专题】存在型． 【分析】先估算出 的值，再比较出其大小即可． 【解答】解：∵ ≈2.236， =2.5， ∴ ＞ ＞2． 故答案为： ＞ ＞2． 【点评】本题考查的是实数的大小比较，熟记 ≈2.236 是解答此题的关键． 29． 的整数部分是 3 ． 【考点】估算无理数的大小． 【分析】根据平方根的意义确定 的范围，则整数部分即可求得． 【解答】解：∵9＜13＜16， ∴3＜ ＜4， ∴ 的整数部分是 3． 故答案是：3． 【点评】本题主要考查了无理数的估算，解题关键是确定无理数的整数部分即可解决问题． 第 15页（共 15页） 30．实数 ﹣2 的整数部分是 3 ． 【考点】估算无理数的大小． 【分析】首先得出 的取值范围，进而得出 ﹣2 的整数部分． 【解答】解：∵5＜ ＜6， ∴ ﹣2 的整数部分是：3． 故答案为：3． 【点评】此题主要考查了估计无理数大小，得出 的取值范围是解题关键．