北师大版数学八年级下册角度计算综合 课后练习一及详解 5页

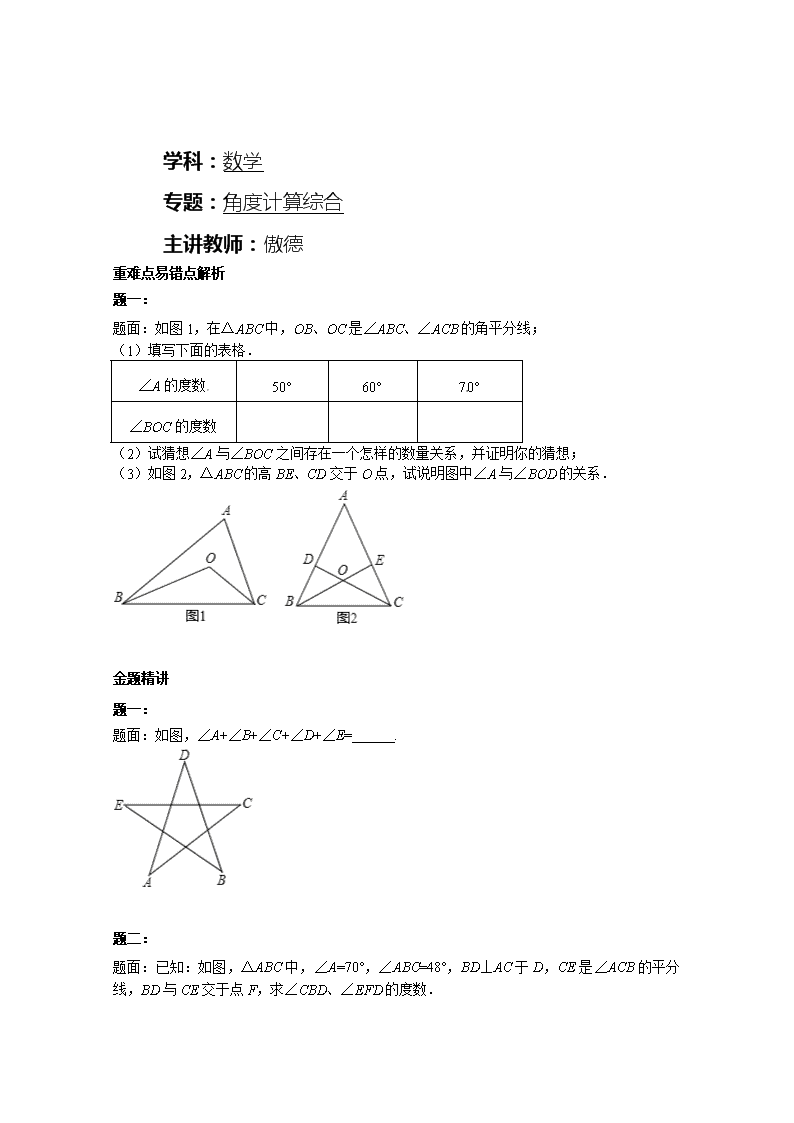
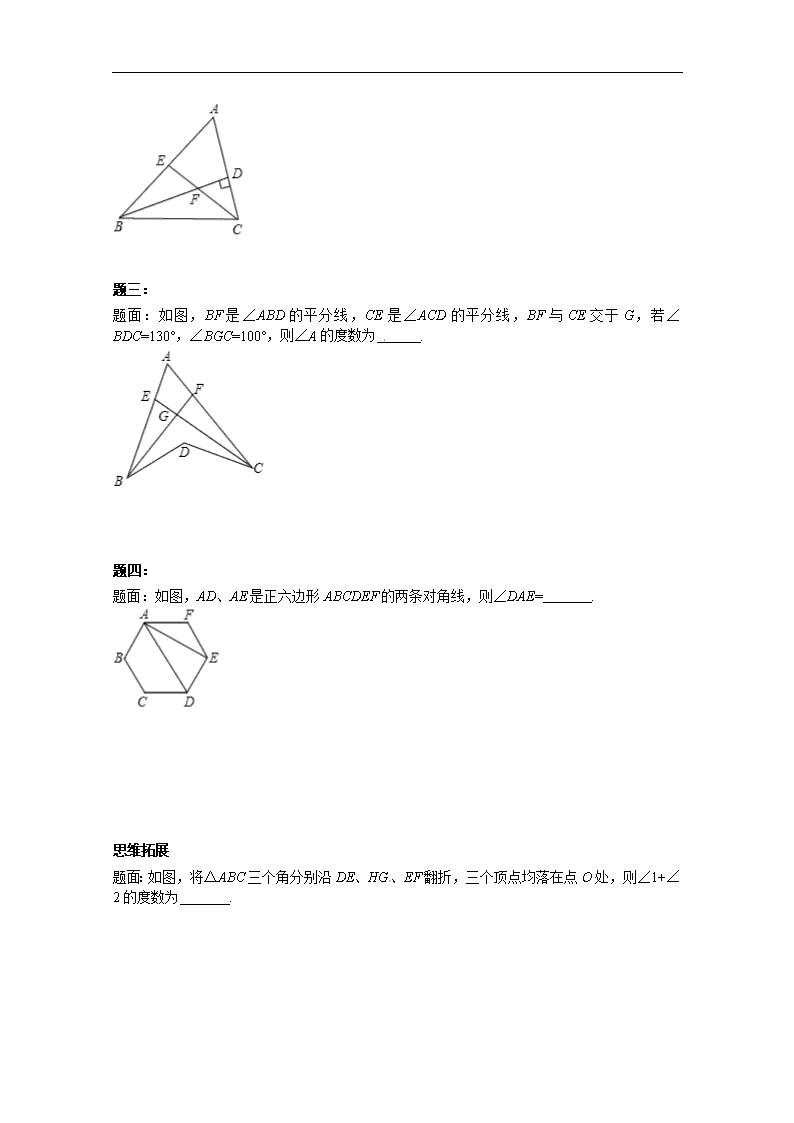
学科：数学 专题：角度计算综合 主讲教师：傲德 重难点易错点解析 题一： 题面：如图 1，在△ABC 中，OB、OC 是∠ABC、∠ACB 的角平分线； （1）填写下面的表格． ∠A 的度数 50° 60° 70° ∠BOC 的度数 （2）试猜想∠A 与∠BOC 之间存在一个怎样的数量关系，并证明你的猜想； （3）如图 2，△ABC 的高 BE、CD 交于 O 点，试说明图中∠A 与∠BOD 的关系． 金题精讲 题一： 题面：如图，∠A+∠B+∠C+∠D+∠E= . 题二： 题面：已知：如图，△ABC 中，∠A=70°，∠ABC=48°，BD⊥AC 于 D，CE 是∠ACB 的平分 线，BD 与 CE 交于点 F，求∠CBD、∠EFD 的度数． 题三： 题面：如图，BF 是∠ABD 的平分线，CE 是∠ACD 的平分线，BF 与 CE 交于 G，若∠BDC=130°， ∠BGC=100°，则∠A 的度数为 . 题四： 题面：如图，AD、AE 是正六边形 ABCDEF 的两条对角线，则∠DAE= . 思维拓展 题面：如图，将△ABC 三个角分别沿 DE、HG 、EF 翻折，三个顶点均落在点 O 处，则∠1+ ∠2 的度数为 .[来源:www.shulihua.net] 课后练习详解 重难点易错点解析 题一： 答案：（1） ∠A 的度数 50° 60° 70° ∠BOC 的度数 115° 120° 125° （2）猜想：∠BOC=90°+ 1 2 ∠A． （3）∠A =∠BOD． [来源:www.shulihua.net] 详解：：（1） ∠A 的度数 50° 60°[来源:www.shulihua.net] 70° ∠BOC 的度数[来源:www.shulihua.net] 115° 120° 125° （2）猜想：∠BOC=90°+ 1 2 ∠A． 理由：∵在△ABC 中，OB、OC 是∠ABC、∠ACB 的角平分线； ∴∠OBC= 1 2 ∠ABC，∠OCB= 1 2 ∠ACB， ∵∠ABC+∠ACB=180°∠A， ∴∠OBC+∠OCB= 1 2 （∠ABC+∠ACB）= 1 2 （180°∠A）=90° 1 2 ∠A， ∴∠BOC=180°（∠OBC+∠OCB）=180°（90° 1 2 ∠A）=90°+ 1 2 ∠A． （3）证明：∵△ABC 的高 BE、CD 交于 O 点， ∴∠BDC=∠BEA=90°， ∴∠ABE+∠BOD=90°，∠ABE+∠A=90°， ∴∠A=∠BOD． 金题精讲 题一： 答案：180°． 详解：如图所示： ∵∠DGE 是△EGB 的外角，∴∠DGF=∠B+∠E， ∵∠DFG 是△AFC 的外角，∴∠DFG=∠A+∠C， ∵∠DFG+∠DGF+∠D=180°， ∴∠A+∠B+∠C+∠D+∠E=180°． 题二： 答案：28°，121° 详解：∵∠A+∠ABC+∠ACB=180°， ∴∠ACB=180°∠A∠ABC=180°70°48°=62°． ∵BD⊥AC， ∴∠BDC=90°． ∴∠CBD=90°∠ACB=90°62°=28°； ∵CE 是∠ACB 的平分线， ∴∠ACE= 1 2 ∠ACB= 1 2 ×62°=31°． ∴∠EFD=∠ACE+∠BDC=31°+90°=121°． 故答案为：∠CBD、∠EFD 的度数分别为 28°，121° 题三： 答案：70°． 详解：连接 BC． ∵∠BDC=130°， ∴∠DBC+∠DCB=180°130°=50°， ∵∠BGC=100°， ∴∠GBC+∠GCB=180°100°=80°， ∵BF 是∠ABD 的平分线，CE 是∠ACD 的平分线， ∴∠GBD+∠GCD= 1 2 ∠ABD+ 1 2 ∠ACD=30°， ∴∠ABC+∠ACB=110°， ∴∠A=180°110°=70°． 题四： 答案：30°． 详解：如图，设正六边形 ABCDEF 的中心为 O，作出正六边形 ABCDEF 的外接圆⊙O，连接 OE，则∠DOE= 1 6 ×360°=60°， ∴∠DAE= 1 2 ∠DAE=30°． 思维拓展 答案：180° 详解：∵将△ABC 三个角分别沿 DE、HG、E F 翻折，三个顶点均落在点 O 处， ∴∠B=∠HOG，∠A=∠DOE，∠C=∠EOF，∠1+∠2+∠HOG+∠EOF+∠DOE=360°， ∵∠HOG+∠EOF+∠DOE=∠A+∠B+∠C=180°， ∴∠1+∠2=360°180°=180°