数学华东师大版八年级上册教案14-1 第3课时 一定是直角三角形吗 5页

- 1 - 1.2 一定是直角三角形吗 教学目标 【知识与能力】 1．理解勾股定理逆定理的具体内容及勾股数的概念； 2．能根据所给三角形三边的条件判断三角形是否是直角三角形. 【过程与方法】 经历一般规律的探索过程，发展学生的抽象思维能力、归纳能力. 【情感态度价值观】 体验生活中的数学的应用价值，感受数学与人类生活的密切联系，激发学生学数学、用数学 的兴趣. 教学重难点 【教学重点】 理解勾股定理逆定理的具体内容. 【教学难点】 理解勾股定理逆定理的具体内容. 教学过程 第一环节：情境引入 内容： 情境：1．直角三角形中，三边长度之间满足什么样的关系？ 2．如果一个三角形中有两边的平方和等于第三边的平方，那么这个三角形是否 就是直角三角形呢？ 意图：通过情境的创设引入新课，激发学生探究热情. 效果：从勾股定理逆向思维这一情景引入，提出问题，激发了学生的求知欲，为下一环 节奠定了良好的基础. 第二环节：合作探究 内容 1：探究 下面有三组数，分别是一个三角形的三边长 cba ,, ，①5，12，13；②7，24，25；③8， 15，17；并回答这样两个问题： 1．这三组数都满足 2 2 2a b c  吗？ 2．分别以每组数为三边作出三角形，用量角器量一量，它们都是直角三角形吗？学生 分为４人活动小组，每个小组可以任选其中的一组数. 意图：通过学生的合作探究，得出“若一个三角形的三边长 cba ,, ，满足 2 2 2a b c  ， 则这个三角形是直角三角形”这一结论；在活动中体验出数学结论的发现总是要经历观察、 归纳、猜想和验证的过程，同时遵循由“特殊→一般→特殊”的发展规律. 效果：经过学生充分讨论后，汇总各小组实验结果发现：①5，12，13 满足 2 2 2a b c  ， 可以构成直角三角形；②7，24，25 满足 222 cba  ，可以构成直角三角形；③8，15，17 满足 222 cba  ，可以构成直角三角形. - 2 - 从上面的分组实验很容易得出如下结论： 如果一个三角形的三边长 cba ,, ，满足 2 2 2a b c  ，那么这个三角形是直角三角形 内容 2：说理 提问：有同学认为测量结果可能有误差，不同意这个发现.你认为这个发现正确吗？你 能给出一个更有说服力的理由吗？ 意图：让学生明确，仅仅基于测量结果得到的结论未必可靠，需要进一步通过说理等方 式使学生确信结论的可靠性，同时明晰结论： 如果一个三角形的三边长 cba ,, ，满足 2 2 2a b c  ，那么这个三角形是直角三角形. 满足 2 2 2a b c  的三个正整数，称为勾股数. 注意事项：为了让学生确认该结论，需要进行说理，有条件的班级，还可利用几何画板 动画演示，让同学有一个直观的认识. 活动 3：反思总结 提问： 1．同学们还能找出哪些勾股数呢？ 2．今天的结论与前面学习勾股定理有哪些异同呢？ 3．到今天为止,你能用哪些方法判断一个三角形是直角三角形呢? 4．通过今天同学们合作探究，你能体验出一个数学结论的发现要经历哪些过程呢？ 意图：进一步让学生认识该定理与勾股定理之间的关系 第三环节：小试牛刀 内容： 1．下列哪几组数据能作为直角三角形的三边长？请说明理由. ①9，12，15； ②15，36，39； ③12，35，36； ④12，18，22 解答：①② 2．一个三角形的三边长分别是 cmcmcm 25,20,15 ，则这个三角形的面积是（ ） A 250 2cm B 150 2cm C 200 2cm D 不能确定 解答：B 3．如图，在 ABC 中， BCAD  于 D ， 20,12,9  ACADBD ，则 ABC 是（ ） A 等腰三角形 B 锐角三角形 C 直角三角形 D 钝角三角形 解答：C 4．将直角三角形的三边扩大相同的倍数后，得到的三角形是（ ） A 直角三角形 B 锐角三角形 C 钝角三角形 D 不能确定 解答：A 意图：通过练习，加强对勾股定理及勾股定理逆定理认识及应用 效果：每题都要求学生独立完成（5 分钟），并指出各题分别用了哪些知识. 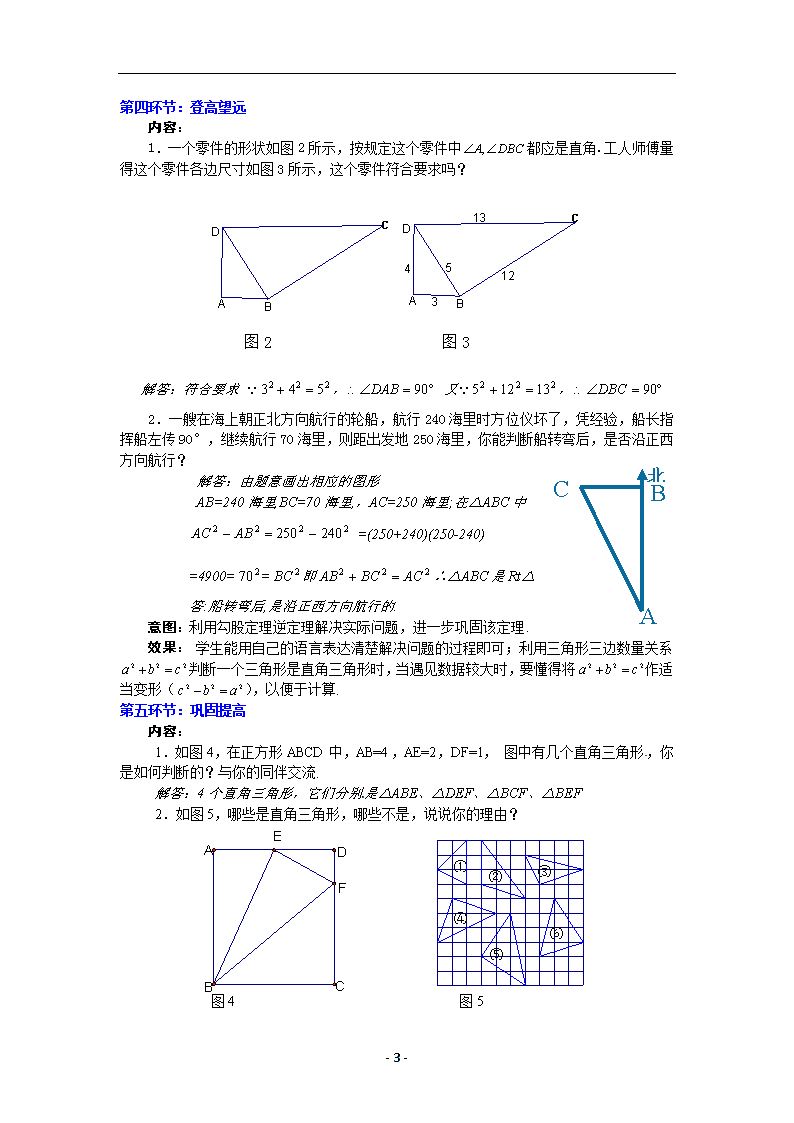D A B C - 3 - F DA B C E A B 北C 第四环节：登高望远 内容： 1．一个零件的形状如图 2 所示，按规定这个零件中 DBCA  , 都应是直角.工人师傅量 得这个零件各边尺寸如图 3 所示，这个零件符合要求吗？ 解答：符合要求  222 543  ，  90DAB 又 222 13125  ，  90DBC 2．一艘在海上朝正北方向航行的轮船，航行 240 海里时方位仪坏了，凭经验，船长指 挥船左传 90°，继续航行 70 海里，则距出发地 250 海里，你能判断船转弯后，是否沿正西 方向航行？ 解答：由题意画出相应的图形 AB=240 海里,BC=70 海里,，AC=250 海里;在△ABC 中 2222 240250  ABAC =(250+240)(250-240) =4900= 270 = 2BC 即 222 ACBCAB  ∴△ABC 是 Rt△ 答:船转弯后,是沿正西方向航行的. 意图：利用勾股定理逆定理解决实际问题，进一步巩固该定理. 效果： 学生能用自己的语言表达清楚解决问题的过程即可；利用三角形三边数量关系 222 cba  判断一个三角形是直角三角形时，当遇见数据较大时，要懂得将 222 cba  作适 当变形（ 222 abc  ），以便于计算. 第五环节：巩固提高 内容： 1．如图 4，在正方形 ABCD 中，AB=4，AE=2，DF=1， 图中有几个直角三角形，你 是如何判断的？与你的同伴交流. 解答：4 个直角三角形，它们分别是△ABE、△DEF、△BCF、△BEF 2．如图 5，哪些是直角三角形，哪些不是，说说你的理由？ 图 4 图 5 图 3图 2 C C 13 12 5 3 4 D A B B A D ① ② ③ ⑥ ⑤ ④ - 4 - 解答：④⑤是直角三角形，①②③⑥不是直角三角形 意图： 第一题考查学 生充分利用所学知识解决问题时，考虑问题要全面，不要漏解；第二题 在于考查学生如何利用网格进行计算，从而解决问题. 效果： 学生在对所学知识有一定的熟悉度后，能够快速做答并能简要说明理由即可.注意防漏 解及网格的应用. 第六环节：交流小结 内容： 师生相互交流总结出： 1．今天所学内容①会利用三角形三边数量关系 222 cba  判断一个三角形是直角三角 形；②满足 222 cba  的三个正整数，称为勾股数； 2．从今天所学内容及所作练习中总结出的经验与方法：①数学是源于生活又服务于生 活的；②数学结论的发现总是要经历观察、归纳、猜想和验证的过程，同时遵循由“特殊→ 一般→特殊”的发展规律；③利用三角形三边数量关系 222 cba  判断一个三角形是直角三 角形时，当遇见数据较大时，要懂得将 222 cba  作适当变形， 222 abc  便于计算. 意图： 鼓励学生结合本节课的学习谈自己的收获和感想，体会到勾股定理及其逆定理的广泛应 用及它们的悠久历史；敢于面 对数学学习中的困难，并有独立克服困难和运用知识解决问 题的成功经验，进一步体会数学的应用价值，发展运用数学的信心和能力，初步形成积极参 与数学活动的意识. 效果： 学生畅所欲言自己的切身感受与实际收获，总结出利用三角形三边数量关系 222 cba  判断一个三角形是直角三角形从古至今在实际生活中的广泛应用. 第七环节：布置作业 课本习题 1．3 第 1，2，4 题. 教学反思： 1．充分尊重教材，以勾股定理的逆向思维模式引入“如果一个三角形的三边长 cba ,, ， 满足 2 2 2a b c  ，是否能得到这个三角形是直角三角形”的问题；充分引用教材中出现的 例题和练习. 2．注重引导学生积极参与实验活动，从中体验任何一个数学结论的发现总是要经历观 察、归纳、猜想和验证的过程，同时遵循由“特殊→一般→特殊”的发展规律. 3．在利用今天所学知识解决实际问题时，引导学生善于对公式变形，便于简便计算. 4．注重对学习新知理解应用偏困难的学生的进一步关注. 5．对于勾股定理的逆定理的论证可根据学生的实际情况做适当调整，不做要求. 由于本班学生整体水平较高，因而本设计教学容量相对较大，教学中，应注意根据自 己班级学生的状况进行适当的删减或调整. - 5 - 附：板书设计 能得到直角三角形吗 情景引入———— 小试牛刀： 登高望远————— 合作探究———— １．—————— １． —————— ２．—————— ２．—————— ３．—————— 课后作业：