- 1.37 MB
- 2021-11-01 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
1
一、平行四边形的性质
平行四边形的边:平行四边形的对边平行且对边相等.
平行四边形的角:平行四边形的对角相等,邻角互补.
平行四边形的对角线:平行四边形的对角线互相平分.
平行四边形的对称性:平行四边形是中心对称图形.
平行四边形的周长:一组邻边之和的 2 倍.
平行四边形的面积:底乘以高.
二、平行四边形的判定
两组对边分别平行的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
两条对角线互相平分的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形.
例题精讲
一、平行四边形的性质
【例 1】 如图所示,已知四边形 ABCD ,从⑴ AB DC∥ ;⑵ AB DC ;⑶ AD BC∥ ;⑷ AD BC ;⑸
A C ;⑹ B D 中取两个条件加以组合,能推出四边形 ABCD 是平行四边形的有哪几种
情形?请写出具体组合。
�
A
�
D
�
B
�
C
【解析】 本题 6 个条件中任取 2 个,共有 15 种组合情形,其中能证明是平行四边形的有 9 种情况:
① ⑴,⑶;② ⑵,⑷;③ ⑸,⑹;④ ⑴,⑵;
⑤ ⑶,⑷;⑥ ⑴,⑸;⑦ ⑴,⑹;⑧ ⑶,⑸;⑨ ⑶,⑹.
【答案】① ⑴,⑶;② ⑵,⑷;③ ⑸,⑹;④ ⑴,⑵;
⑤ ⑶,⑷;⑥ ⑴,⑸;⑦ ⑴,⑹;⑧ ⑶,⑸;⑨ ⑶,⑹.
【例 2】 如图,在平行四边形 ABCD 中, EF BC GH AB EF∥ , ∥ , 与 GH 相交于点O ,图中共有 个
平行四边形
内容 基本要求 略高要求 较高要求
平行四边形 会识别平行四边形
掌握平行四边形的概念、判定和性质,
会用平行四边形的性质及判定解决简
单问题
会运用平行四边形
的性质及判定解决
有关问题
平行四边形
2
【解析】省略
【答案】 9 个
【例 3】 以三角形的三个顶点作平行四边形,最多可以作( )
A.2 个 B.3 个 C.4 个 D.5 个
【解析】省略
【答案】B
【例 4】 如图,在平行四边 ABCD 中, AC 、 BD 为对角线, 6BC , BC 边上的高为 4 ,则阴影部分的
面积为( ).
A.3 B.6 C.12 D.24
【解析】利用平行线的性质及割补法可得 C.
【答案】C
【例 5】 如图,在平行四边 ABCD 中,已知 8cmAD , 6cmAB , DE 平分 ADC
交 BC 边于点 E ,则 BE 等于 cm .
【解析】过E 作EF AB∥ 交 AD 于点F,由于DE 平分 ADC ,有 ADE EDC CED FED
即, 6EF FD EC AB ,即 2BE AF AD AF
【答案】见解析
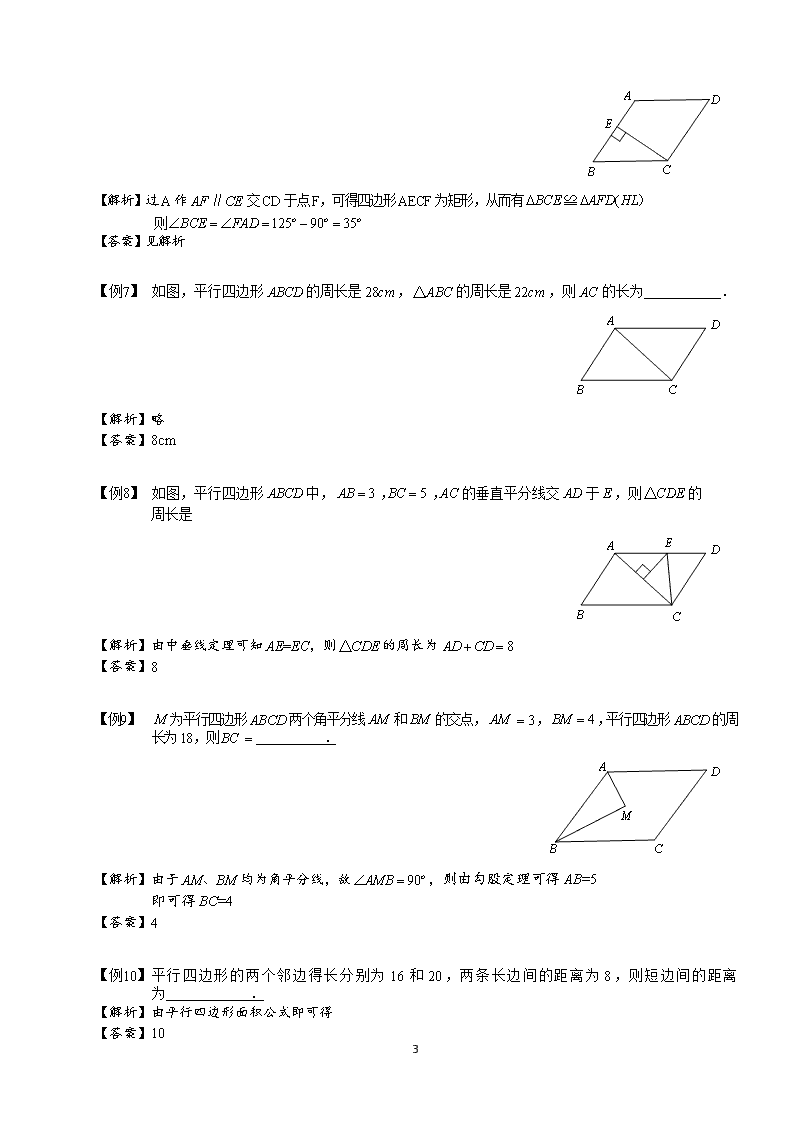
【例 6】 如图,在平形四边形 ABCD 中, CE AB , E 为垂足.如果 125A ,则 BCE .
3
【解析】过A 作 AF CE∥ 交CD 于点F,可得四边形AECF 为矩形,从而有 (BCE AFD HL ≌ )
则 125 90 35o o oBCE FAD
【答案】见解析
【例 7】 如图,平行四边形 ABCD 的周长是 28cm , ABC△ 的周长是 22cm ,则 AC 的长为 .
【解析】略
【答案】8cm
【例 8】 如图,平行四边形 ABCD 中, 3 5AB BC AC , , 的垂直平分线交 AD 于 E ,则 CDE△ 的
周长是
【解析】由中垂线定理可知 AE=EC,则 CDE△ 的周长为 8AD CD
【答案】8
【例9】 M 为平行四边形 ABCD 两个角平分线 AM 和BM 的交点,AM 3 , 4BM ,平行四边形 ABCD 的周
长为18,则BC .
【解析】由于 AM、BM 均为角平分线,故 90oAMB ,则由勾股定理可得 AB=5
即可得 BC=4
【答案】4
【例 10】 平行四边形的两个邻边得长分别为 16 和 20,两条长边间的距离为 8,则短边间的距离
为 .
【解析】由平行四边形面积公式即可得
【答案】10
4
【例 11】 如图,在平行四边形 ABCD 中, AE BC 于 E , AF CD 于 F ,若 4, 6AE AF ,平行四
边形的周长为 40,则平行四边形 ABCD 的面积为 。
【解析】连接 AC,将平行四边形面积分为两个面积相等的三角形的面积和
可设 BC x ,则 20CD x ,有 4 6(20 )x x ,可得 12BC , 8CD
则平行四边形的面积为:(12 4) / 2 (8 6) / 2 48
【答案】48
【例 12】 如图,平行四边形 ABCD 中,BE CD 于 E ,BF AD 于点 F , 2, 1, 60 ,CE DF EBF
则平行四边形 ABCD 的面积为 。
【解析】由于 60EBF 且 BE CD ,则 30ABF , 60A , 30EBC
又有 2CE ,可得 4CB 。又由 1DF ,可得 3 3BF
则平行四边形的面积为: 4 3 3 12 3
【答案】12 3
【例 13】 如图,点 E F, 是平行四边形 ABCD 对角线上的两点,且 BE DF ,那么 AF 和CE 相等吗?
请说明理由
【解析】因为 ABCD 是平行四边形
所以 AD BC AD BC , ∥
所以 1 2 ,又因为 1 180ADF , 2 180EBC
所以 ADF EBC
又因为 BE DF ,
所以 ADF CBE ≌ ,所以 AF CE
【答案】 AF CE
【例 14】 已知如图:平行四边形 ABCD 中, CN AM , AE CF ,求证:四边形 MENF 是平行四边
5
形.
【解析】 AME△ CFN≌△ ,得到 ,NF EM EF EM ∥ ,即四边形 MENF 是平行四边形
【答案】略
【例 15】 已知如图: BAD DAC , BE MN∥ , BN EM∥ ,求证: AM BN .
【解析】 BE MN∥ ,BN EM∥ ,四边形 BNME 为平行四边形,平行加角平分线得出 AME△ 为等腰三角
形,然后根据 NB ME ,故 AM BN
【答案】略
【例 16】 如图, ,E F 是平行四边形 ABCD 的对角线 AC 上的两点, AE CF .
求证:(1) ADF ≌ CBE ;
(2) EB DF∥ .
�
A
�
F
�
E
�
D
�
C
�
B
【解析】(1)∵ AE CF ,
∴ AE EF CF FE ,即 AF CE .
又∵ ABCD 是平行四边形,
∴ ,AD CB AD BC ∥ .
∴ DAF BCE .
∴ ADF ≌ CBE
(2)∵ ADF ≌ CBE
∴ DFA BEC .
∴DF EB∥ .
【答案】(1)∵ AE CF ,
∴ AE EF CF FE ,即 AF CE .
又∵ ABCD 是平行四边形,
∴ ,AD CB AD BC ∥ .
∴ DAF BCE .
∴ ADF ≌ CBE
(2)∵ ADF ≌ CBE
∴ DFA BEC .
6
∴DF EB∥ .
【例 17】 如图,已知:在平行四边形 ABCD 中, BCD 的平分线CE 交边 AD 于 E , ABC 的平分线 BG
交 CE 于 F ,交 AD 于G .求证: AE DG .
�
F
�
G
�
E
�
D
�
C
�
B
�
A
【解析】⑴ ①(答案不惟一)
⑵ ∵四边形 ABCD 是平行四边形(已知)
∴ AD BC∥ , AB CD (平行四边形的对边平行且相等)
∴ GBC BGA , BCE CED (两直线平行,内错角相等)
又∵ BG 平分 ABC ,CE 平分 BCD (已知)
∴ ABG GBC , BCE ECD (角平分线定义)
∴ ABG AGB , ECD CED .
∴ AB AG , CE DE (在同一个三角形中,等角对等边)
∴ AG DE
∴ AG EG DE EG ,即 AE DG
【答案】⑴ ①(答案不惟一)
⑵ ∵四边形 ABCD 是平行四边形(已知)
∴ AD BC∥ , AB CD (平行四边形的对边平行且相等)
∴ GBC BGA , BCE CED (两直线平行,内错角相等)
又∵ BG 平分 ABC ,CE 平分 BCD (已知)
∴ ABG GBC , BCE ECD (角平分线定义)
∴ ABG AGB , ECD CED .
∴ AB AG , CE DE (在同一个三角形中,等角对等边)
∴ AG DE
∴ AG EG DE EG ,即 AE DG
课后作业
【习题 1】如图,四边形 ABCD 为平行四边形,即 AB CD∥ , AD BC∥ .通过证明三角形全等来说明:
⑴ AB CD , AD BC .(对边相等)
⑵ AO CO , BO DO .(对角线互相平分)
�
O
�
D
�
C
�
B
�
A
【解析】省略
【答案】⑴ ∵ AB CD∥ , AD BC∥
∴ ABD CDB , ADB CBD
在 ABD 和 CDB 中,
ABD CDB
BD DB
ADB CBD
7
∴ ABD CDB ≌
∴ AB CD , AD BC .
⑵ 在 ABO 和 CDO 中,
ABO CDO
AOB COD
AB CD
∴ AO CO , BO DO .
【习题 2】在平行四边形 ABCD 中,点 1A 、 2A 、 3A 、 4A 和 1C 、 2C 、 3C 、 4C 分别为 AB 和 CD 的五等分点,
点 1B 、 2B 和 1D 、 2D 分别是 BC 和 DA 的三等分点,已知四边形 4 2 4 2A B C D 的面积为1,则平行四
边形 ABCD 面积为( )
A.2 B. 3
5 C. 5
3 D.15
【解析】利用对称性、平行线的性质及割补法可得 C.
【答案】C
【习题 3】如图,已知: AD 是 ABC 的角平分线, DE AB∥ ,在 AB 上截取 BF AE ,连接 DE EF, ,求
证:四边形 BDEF 是平行四边形
【解析】省略
【答案】因为 AD 平分 BAC
所以 BAD CAD
因为 DE AB∥ ,所以 BAD ADE
所以 EAD ADE DE AE ,
因为 BF AE ,所以 DE BF
因为 DE BF∥ ,所以 BDEF 是平行四边形
【习题 4】如图, ABC 中, D 是 AB 的中点, E 是 AC 上任意一点, EF ∥ AB , DF ∥ BE .求证: DF
与 AE 互相平分.
8
【解析】省略
【答案】连结 AF 、 DE .
∵ EF ∥ AB , DF ∥ BE ,∴四边形 BDFE 是平行四边形
∴ EF BD
∵ AD BD ,∴ AD EF
∵ AD ∥ EF ,∴四边形 ADEF 是平行四边形
∴ DF 与 AE 互相平分
相关文档
- 2020年八年级语文上册 第二单元 82021-11-012页
- 2019八年级数学下册11.2反比例函数2021-11-015页
- 2019八年级语文上册 第六单元 20愚2021-11-013页
- 2019年八年级道德与法治上册第2单2021-11-016页
- 2020八年级物理上册探究光的折射规2021-11-014页
- 2020年八年级语文上册 第五单元 第2021-11-011页
- 部编版八年级语文上册第6单元主题2021-11-0130页
- 2020八年级道德与法治上册第二单元2021-11-014页
- 2020年八年级道德与法治上册 第四2021-11-013页
- 部编版八年级下册语文《庄子》二则2021-11-014页