- 79.50 KB
- 2021-11-01 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
微专题:矩形中的典型模型问题
模型一 面积问题
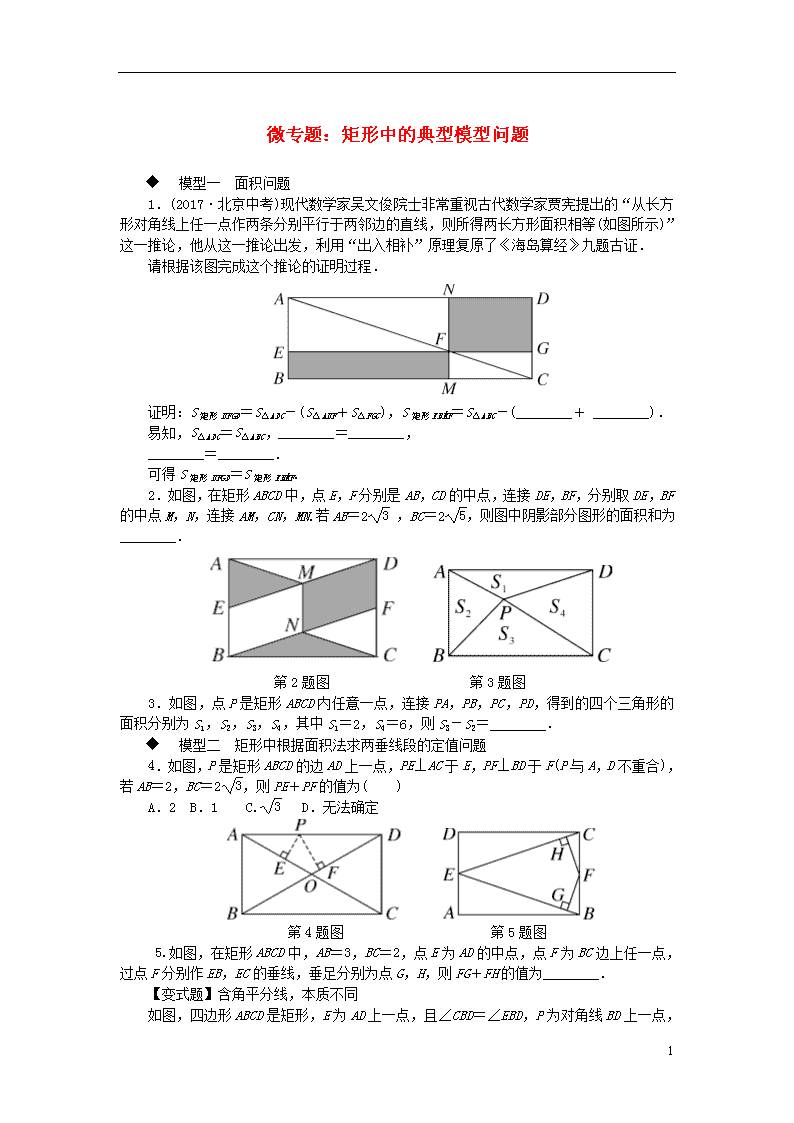
1.(2017·北京中考)现代数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所得两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.
请根据该图完成这个推论的证明过程.
证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC),S矩形EBMF=S△ABC-(________+ ________).
易知,S△ADC=S△ABC,________=________,
________=________.
可得S矩形NFGD=S矩形EBMF.
2.如图,在矩形ABCD中,点E,F分别是AB,CD的中点,连接DE,BF,分别取DE,BF的中点M,N,连接AM,CN,MN.若AB=2 ,BC=2,则图中阴影部分图形的面积和为________.
第2题图 第3题图
3.如图,点P是矩形ABCD内任意一点,连接PA,PB,PC,PD,得到的四个三角形的面积分别为S1,S2,S3,S4,其中S1=2,S4=6,则S3-S2=________.
模型二 矩形中根据面积法求两垂线段的定值问题
4.如图,P是矩形ABCD的边AD上一点,PE⊥AC于E,PF⊥BD于F(P与A,D不重合),若AB=2,BC=2,则PE+PF的值为( )
A.2 B.1 C. D.无法确定
第4题图 第5题图
5.如图,在矩形ABCD中,AB=3,BC=2,点E为AD的中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH的值为________.
【变式题】含角平分线,本质不同
如图,四边形ABCD是矩形,E为AD上一点,且∠CBD=∠EBD,P为对角线BD上一点,
3
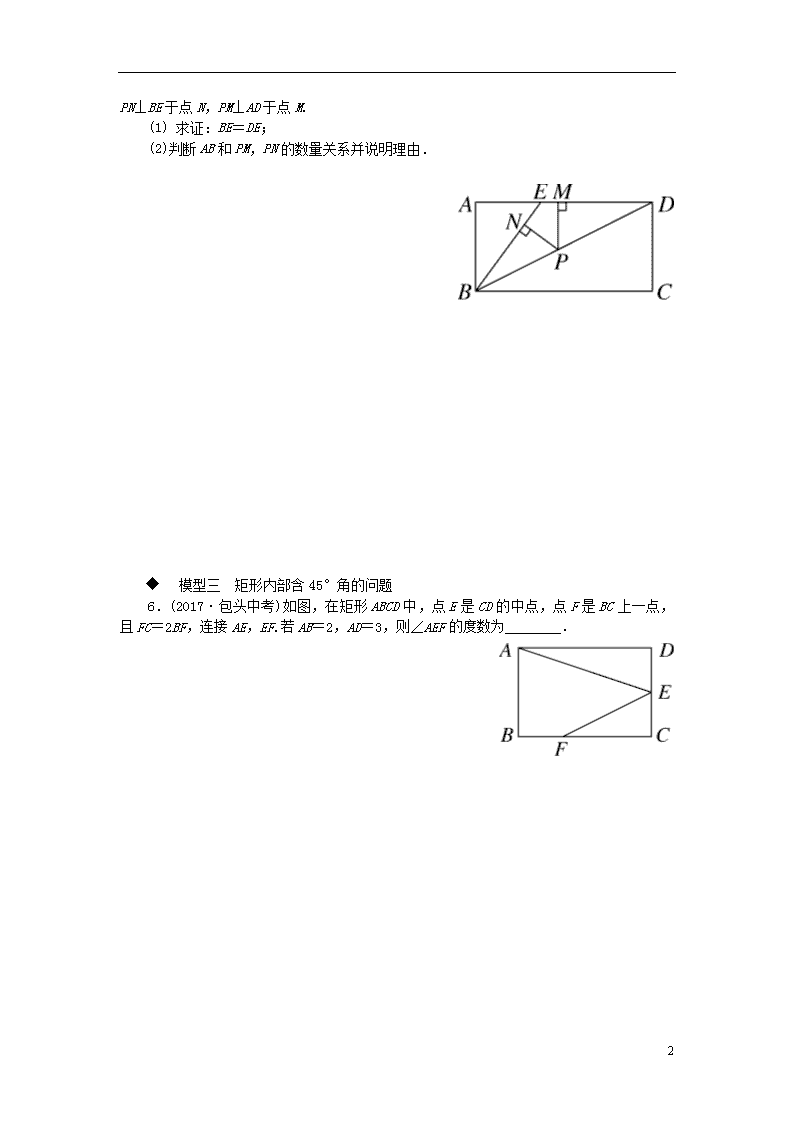
PN⊥BE于点N,PM⊥AD于点M.
(1) 求证:BE=DE;
(2)判断AB和PM,PN的数量关系并说明理由.
模型三 矩形内部含45°角的问题
6. (2017·包头中考)如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则∠AEF的度数为________.
3
参考答案与解析
1.S△AEF S△FCM S△ANF S△AEF S△FGC S△FMC
2.2
3.4 解析:∵四边形ABCD是矩形,∴AB=CD,AD=BC.设点P到AD,AB,BC,CD的距离分别为h1,h2,h3,h4,则S1=AD·h1,S2=AB·h2,S3=BC·h3,S4=CD·h4.∵AD·h1+BC·h3=BC·CD,AB·h2+CD·h4=AB·BC,∴AD·h1+BC·h3=AB·h2+CD·h4,即∴S2+S4=S1+S3,∴S3-S2=S4-S1=6-2=4.
4.C
5. 解析:连接EF.∵四边形ABCD是矩形,∴CD=AB=3,AD=BC=2,∠A=∠D=90°.∵点E为AD的中点,∴AE=DE=1.在Rt△ABE中,BE===,在Rt△DCE中,CE===,∴BE=CE=.∵S△BCE=S△BEF+S△CEF,∴BC·AB=BE·FG+CE·FH,即BE(FG+FH)=BC·AB,∴(FG+FH)=2×3,解得FG+FH=.
【变式题】
(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠ADB=∠CBD,∵∠CBD=∠EBD,∴∠ADB=∠EBD,∴BE=DE.
(2) 解:AB=PM+PN.理由如下:如图,延长MP交BC于Q.∵AD∥BC,PM⊥AD,∴PQ⊥BC.∵∠CBD=∠EBD,PN⊥BE,∴PQ=PN,∴AB=MQ=PM+PQ=PM+PN.
6.45° 解析:连接AF.∵四边形ABCD是矩形,∴∠B=∠C=90°,CD=AB=2,BC=AD=3.∵FC=2BF,∴BF=1,FC=2,∴AB=FC.∵E是CD的中点,∴CE=CD=1,∴BF=CE.在△ABF和△FCE中,∴△ABF≌△FCE(SAS),∴∠BAF=∠CFE,AF=FE.∵∠BAF+∠AFB=90°,∴∠CFE+∠AFB=90°,∴∠AFE=180°-90°=90°,∴△AEF是等腰直角三角形,∴∠AEF=45°.
3
相关文档
- 初中数学8年级教案:第12讲 特殊的平2021-11-0110页
- 重庆市巴蜀中学初中部数学教研组整2021-11-0127页
- 重庆市巴蜀中学初中部数学教研组整2021-11-0134页
- 人教版初中语文8年级上册:第6单元 2021-11-0119页
- 初中数学8年级教案:第10讲 平行四边2021-11-018页
- 人教版初中语文8年级上册:第2单元 2021-11-0118页
- 初中8年级语文教案:第8讲 期中考试2021-11-0111页
- 沪科版初中物理知识点汇总2021-11-0172页
- 北师大版数学初中八年级上册课件-2021-11-0120页
- 初中8年级物理教案:第09讲 功率2021-11-0111页