沪科版八年级数学上册第15章测试题（含答案） 10页

沪科版八年级数学上册第15章测试题（含答案）‎ ‎(考试时间：120分钟　　　满分：150分)‎ 分数：__________‎ 一、选择题(本大题共10小题，每小题4分，满分40分)‎ 每小题都给出A、B、C、D四个选项，其中只有一个是正确的．‎ ‎1．下列交通标志中，是轴对称图形的是(　C　)‎ ‎ ‎ A　 B　 C　 D ‎2．等腰三角形的两边长分别为5 cm和10 cm，则此三角形的周长是(　C　)‎ A．15 cm B．20 cm C．25 cm D．20 cm或25 cm ‎3．△ABC中，AB＝AC，D为BC边的中点，∠BAD＝35°，则∠C的度数为(　B　)‎ A．70° B．55° C．65° D．35°‎ ‎4．如图，△ABC中，∠B＝60°，AB＝AC，BC＝3，则△ABC的周长为(　A　)‎ A．9 B．8 C．6 D．12‎ ‎ ‎ 第4题图　　 第6题图 ‎5．若有三点A，B，C不在同一条直线上，点P满足PA＝PB＝PC，则平面内这样的点P有(　A　)‎ A．1个 B．2个 C．1个或2个 D．无法确定 ‎6．如图，在△ABC中，∠C＝90°，∠ABC＝60°，BD平分∠ABC，若AD＝6，则CD等于(　A　)‎ 10‎ 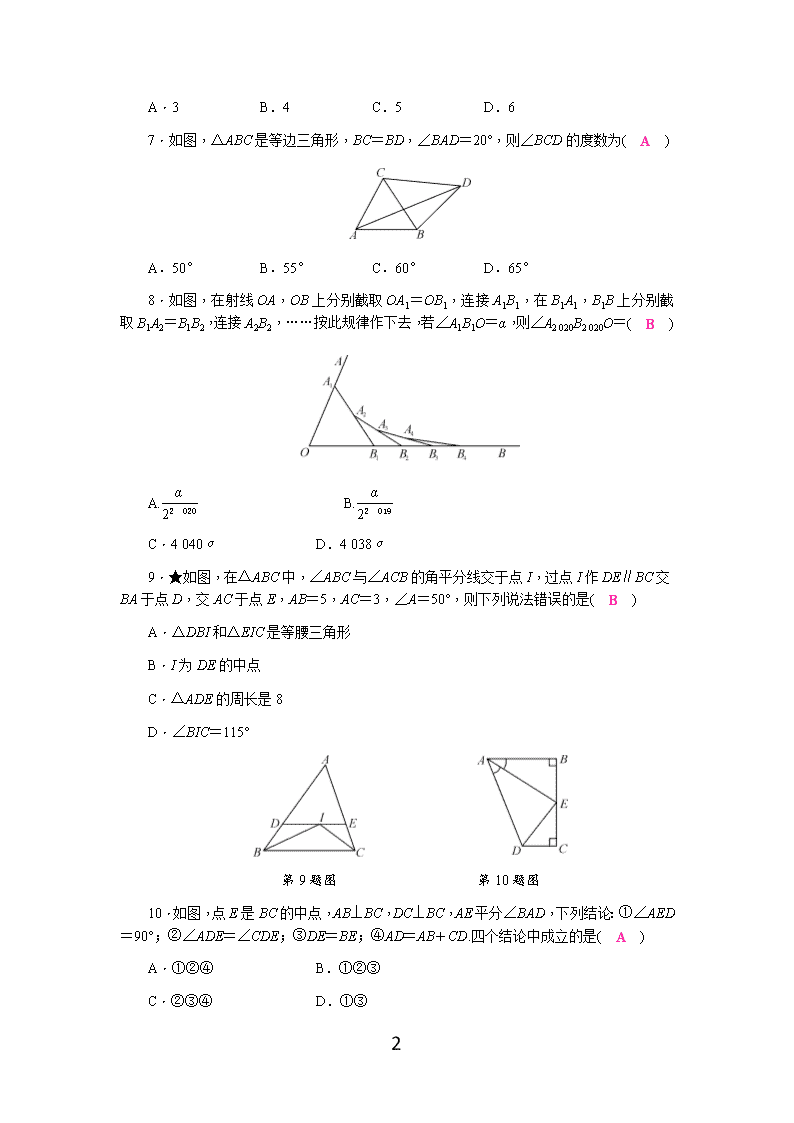A．3 B．4 C．5 D．6‎ ‎7．如图，△ABC是等边三角形，BC＝BD，∠BAD＝20°，则∠BCD的度数为(　A　)‎ A．50° B．55° C．60° D．65°‎ ‎8．如图，在射线OA，OB上分别截取OA1＝OB1，连接A1B1，在B1A1，B1B上分别截取B1A2＝B1B2，连接A2B2，……按此规律作下去，若∠A1B1O＝α，则∠A2 020B2 020O＝(　B　)‎ A. B. C．4 040α D．4 038α ‎9．★如图，在△ABC中，∠ABC与∠ACB的角平分线交于点I，过点I作DE∥BC交BA于点D，交AC于点E，AB＝5，AC＝3，∠A＝50°，则下列说法错误的是(　B　)‎ A．△DBI和△EIC是等腰三角形 B．I为DE的中点 C．△ADE的周长是8‎ D．∠BIC＝115°‎ ‎ ‎ 第9题图　　　 第10题图 ‎10．如图，点E是BC的中点，AB⊥BC，DC⊥BC，AE平分∠BAD，下列结论：①∠AED＝90°；②∠ADE＝∠CDE；③DE＝BE；④AD＝AB＋CD.四个结论中成立的是(　A　)‎ A．①②④ B．①②③‎ C．②③④ D．①③‎ 10‎ 二、填空题(本大题共4小题，每小题5分，满分20分)‎ ‎11．点P(5，－3)关于x轴的对称点P′的坐标是 (5，3) ．‎ ‎12．如图，在△ABC中，分别以点A和点B为圆心，大于AB的长为半径画弧，两弧相交于M，N，作直线MN，交BC于点D，连接AD.如果BC＝5，CD＝2，那么AD＝ 3 .‎ ‎ ‎ 第12题图　　　 第14题图 ‎13．如图，在三角形纸片ABC中，∠C＝90°，∠B＝30°，点D(不与B，C重合)是BC上任意一点，将此三角形纸片按下列方式折叠，若EF的长度为5 cm，则△DEF的周长为 15cm .‎ ‎14．★(蚌埠期末)如图，等腰三角形底边BC的长为6，面积是24，腰AB的垂直平分线EF交AC于点F，D为BC边上的中点，M为线段EF上一动点，则△BDM的周长最短为 11 .‎ 选择、填空题答题卡 一、选择题(每小题4分，共40分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 得分 答案 C C B A A 题号 ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 A A B B A 二、填空题(每小题5分，共20分)得分：______‎ ‎11．__(5，3)__　　12. 3 ‎ ‎13． 15cm 　 14. 11 ‎ 三、(本大题共2小题，每小题8分，满分16分)‎ 10‎ ‎15．(合肥包河区期末)如图，已知△ABC.‎ ‎(1)画出△ABC的高AD；‎ ‎(2)用尺规作出△ABC的角平分线BE(要求保留作图痕迹，不用证明)．‎ 解：(1)如图，AD即为△ABC的高．‎ ‎(2)如图，BE即为△ABC的角平分线．‎ ‎16．如图，在正方形网格上有一个△ABC.‎ ‎(1)作△ABC关于直线MN的对称图形(不写作法)；‎ ‎(2)若网格上的最小正方形的边长为1，求△ABC的面积．‎ 解：(1)分别作A，B，C关于MN的对称点，顺次连接，如图所示．‎ ‎(2)此三角形面积为 S△ABC＝S矩形DECF－S△ABD－S△ACF－S△BEC ‎＝2×3－2×－×1×3‎ ‎＝6－2－ 10‎ ‎＝.‎ 四、(本大题共2小题，每小题8分，满分16分)‎ ‎17．如图，△ABC中，AD为角平分线，DE⊥AB于E，DF⊥AC于F，AB＝10 cm，AC＝8 cm，△ABC的面积为54 cm2，求DE的长．‎ 解：∵AD为角平分线，DE⊥AB于E，DF⊥AC于F，‎ ‎∴DE＝DF.‎ ‎∵△ABC的面积为54 cm2，‎ ‎∴AB·DE＋AC·DF＝54.‎ ‎∵AB＝10 cm，AC＝8 cm，‎ ‎∴×10×DE＋×8×DE＝54，‎ 解得DE＝6 cm.‎ ‎∴DE的长为6 cm.‎ ‎18．如图，已知AB＝AC＝AD，且AD∥BC，求证：∠C＝2∠D.‎ 证明：∵AB＝AC＝AD，‎ ‎∴∠C＝∠ABC，‎ ‎∠D＝∠ABD，‎ 10‎ ‎∴∠ABC＝∠CBD＋∠D.‎ ‎∵AD∥BC，‎ ‎∴∠CBD＝∠D，‎ ‎∴∠ABC＝∠D＋∠D＝2∠D.‎ ‎∵∠C＝∠ABC，‎ ‎∴∠C＝2∠D.‎ 五、(本大题共2小题，每小题10分，满分20分)‎ ‎19．(潜山期末)在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．试作出图形，写出已知、求证，并给出证明．‎ 解：已知：如图，‎ Rt△ABC中，∠A＝30°，∠ACB＝90°，‎ 求证：BC＝AB.‎ 证明：延长BC到D，使CD＝BC，连接AD， ‎∴Rt△ACB≌Rt△ACD，(SAS)‎ ‎∴AD＝AB，∠BAD＝60°.‎ ‎∴△ABD为等边三角形，‎ ‎∴AB＝BD，‎ ‎∴BC＝CD＝AB，即BC＝AB.‎ ‎20．(杭州中考)在△ABC中，AC＜AB＜BC.‎ 10‎ ‎(1)如图①，已知线段AB的垂直平分线与BC边交于点P，连接AP，求证：∠APC＝2∠B；‎ ‎(2)如图②，以点B为圆心，线段AB的长为半径画弧，与BC边交于点Q，连接AQ.若∠AQC＝3∠B，求∠B的度数．‎ ‎　　　 ①　　　　　　　　　　②‎ ‎(1)证明：∵线段AB的垂直平分线与BC边交于点P，‎ ‎∴PA＝PB，‎ ‎∴∠B＝∠BAP.‎ ‎∵∠APC＝∠B＋∠BAP，‎ ‎∴∠APC＝2∠B.‎ ‎(2)解：根据题意可知BA＝BQ，‎ ‎∴∠BAQ＝∠BQA.‎ ‎∵∠AQC＝3∠B，∠AQC＝∠B＋∠BAQ，‎ ‎∴∠BAQ＝∠BQA＝2∠B.‎ ‎∵∠BAQ＋∠BQA＋∠B＝180°，‎ ‎∴5∠B＝180°，∴∠B＝36°.‎ 六、(本题满分12分)‎ ‎21．如图，在5×5正方形网格中，有线段AB和直线MN.‎ ‎(1)在MN上找一点C，使△ABC的周长最小；‎ ‎(2)在网格中作出点P，使△ABP是以AB为腰的等腰三角形，且点P要在格点上，则这样的点P有多少个？‎ ‎ ‎ 10‎ 题图 答图① 答图②‎ 解：(1)如答图①，过点B作B关于直线MN的对称点D，连接AD交MN于C，‎ 则此时△ABC的周长最小．‎ ‎(2)如答图②所示．‎ 当BA＝BP时，符合条件的点有：Q，Z，E，L，F，W共6个，‎ 当AB＝AP时，符合条件的点有：T，G，H共3个．‎ 答：这样的点P有9个．‎ 七、(本题满分12分)‎ ‎22．已知：点O到△ABC的两边AB，AC所在直线的距离相等，且OB＝OC.‎ ‎(1)如图①，若点O在边BC上，求证：AB＝AC；‎ ‎(2)如图②，若点O在△ABC的内部，求证：AB＝AC；‎ ‎(3)若点O在△ABC的外部，AB＝AC成立吗？请画出图表示．‎ ‎(1)证明：过点O分别作OE⊥AB于E，OF⊥AC于F，‎ 由题意知，‎ 在Rt△OEB和Rt△OFC中，‎ ‎∴Rt△OEB≌Rt△OFC，(HL)‎ ‎∴∠ABC＝∠ACB，‎ ‎∴AB＝AC.‎ ‎(2)证明：过点O分别作OE⊥AB于E，OF⊥AC于F，‎ 由题意知，OE＝OF.∠BEO＝∠CFO＝90°，‎ 在Rt△OEB和Rt△OFC中，‎ 10‎ ‎∴Rt△OEB≌Rt△OFC，(HL)‎ ‎∴∠OBE＝∠OCF.‎ 又∵OB＝OC，‎ ‎∴∠OBC＝∠OCB，‎ ‎∴∠ABC＝∠ACB，‎ ‎∴AB＝AC.‎ ‎(3)解：不一定成立，当∠A的平分线所在直线与边BC的垂直平分线重合时AB＝AC，否则AB≠AC.(如示例图)‎ 八、(本题满分14分)‎ ‎23．如图，△ABC是边长为6的等边三角形，P是AC边上一动点，由A向C运动(与A，C不重合)，Q是CB延长线上一动点，与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合)，过P作PE⊥AB于E，连接PQ交AB于D.‎ ‎(1)若AE＝1时，求AP的长；‎ ‎(2)当∠BQD＝30°时，求AP的长；‎ ‎(3)在运动过程中线段ED的长是否发生变化？如果不变，求出线段ED的长；如果发生变化，请说明理由．‎ 解：(1)∵△ABC是等边三角形，‎ ‎∴∠A＝60°.‎ 10‎ ‎∵PE⊥AB，‎ ‎∴∠APE＝30°.‎ ‎∵AE＝1，∠APE＝30°，PE⊥AB，‎ ‎∴AP＝2AE＝2.‎ ‎(2)过点P作PF∥QC，‎ 则△AFP是等边三角形．‎ ‎∵P，Q同时出发，速度相同，即BQ＝AP，‎ ‎∴BQ＝PF.‎ 在△DBQ和△DFP中，‎ ‎∴△DBQ≌△DFP，(AAS)‎ ‎∴BD＝DF.‎ ‎∵∠BQD＝∠BDQ＝∠FDP＝∠FPD＝30°，‎ ‎∴BD＝DF＝FA＝AB＝2，‎ ‎∴AP＝2.‎ ‎(3)线段ED的长不发生变化，理由：‎ 由(2)知BD＝DF，‎ ‎∵△AFP是等边三角形，PE⊥AB，‎ ‎∴AE＝EF，‎ ‎∴DE＝DF＋EF＝BF＋FA＝AB＝3为定值，即ED的长不变．‎ 10‎