2019四川省遂宁市中考数学试卷（Word版，含答案） 26页

2019 年四川省遂宁市中考数学试卷 一、选择题（本大题共 10 个小题，每小题 4 分，共 40 分，在每个小题给出的四个选项中，只有一个符合题目要求.） 1．（4 分）﹣|﹣ |的值为（ ） A． B．﹣ C．± D．2 2．（4 分）下列等式成立的是（ ） A．2+ ＝2 B．（a2b3）2＝a4b6 C．（2a2+a）÷a＝2a D．5x2y﹣2x2y＝3 3．（4 分）如图为正方体的一种平面展开图，各面都标有数字，则数字为﹣2 的面与其对面上的数字 之积是（ ） A．﹣12 B．0 C．﹣8 D．﹣10 4．（4 分）某校为了了解家长对“禁止学生带手机进入校园”这一规定的意见，随机对全校 100 名学生家长进行调查， 这一问题中样本是（ ） A．100 B．被抽取的 100 名学生家长 C．被抽取的 100 名学生家长的意见 D．全校学生家长的意见 5．（4 分）已知关于 x 的一元二次方程（a﹣1）x2﹣2x+a2﹣1＝0 有一个根为 x＝0，则 a 的值为（ ） A．0 B．±1 C．1 D．﹣1 6．（4 分）如图，△ABC 内接于 ⊙ O，若∠A＝45°， ⊙ O 的半径 r＝4，则阴影部分的面积为（ ） A．4 π ﹣8 B．2 π C．4 π D．8 π ﹣8 7．（4 分）如图，▱ ABCD 中，对角线 AC、BD 相交于点 O，OE⊥BD 交 AD 于点 E，连接 BE， 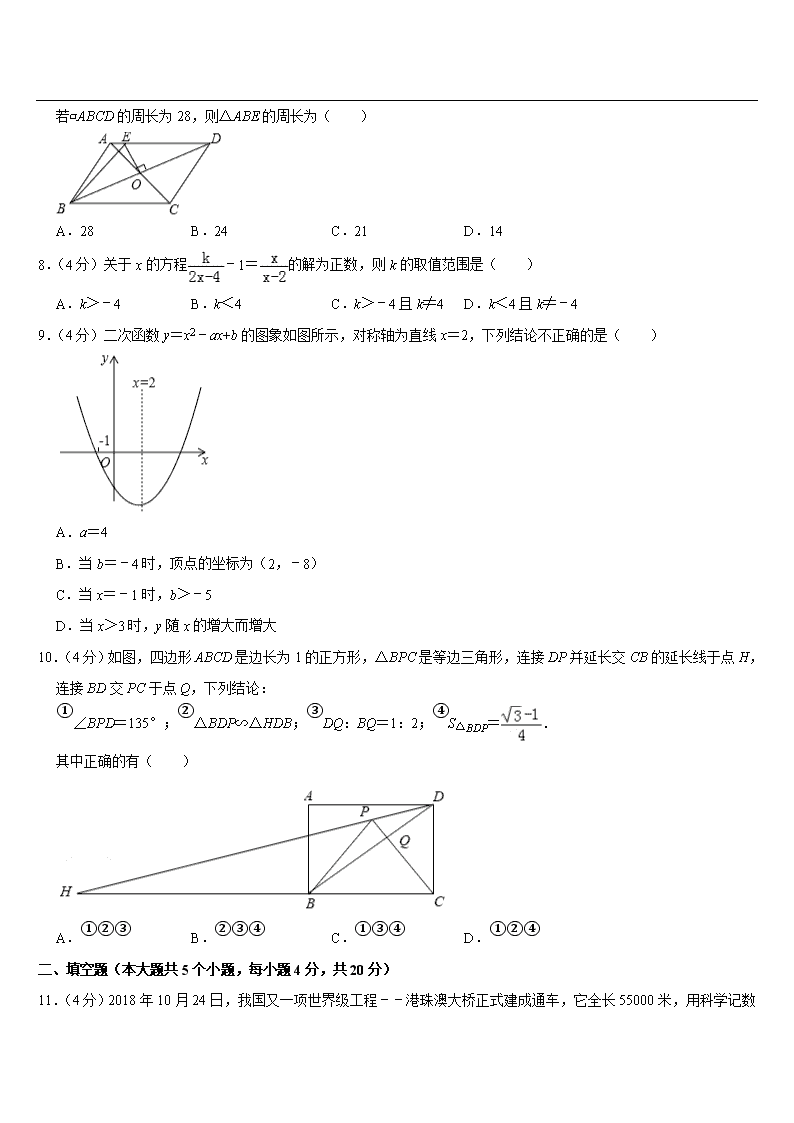若▱ ABCD 的周长为 28，则△ABE 的周长为（ ） A．28 B．24 C．21 D．14 8．（4 分）关于 x 的方程 ﹣1＝ 的解为正数，则 k 的取值范围是（ ） A．k＞﹣4 B．k＜4 C．k＞﹣4 且 k≠4 D．k＜4 且 k≠﹣4 9．（4 分）二次函数 y＝x2﹣ax+b 的图象如图所示，对称轴为直线 x＝2，下列结论不正确的是（ ） A．a＝4 B．当 b＝﹣4 时，顶点的坐标为（2，﹣8） C．当 x＝﹣1 时，b＞﹣5 D．当 x＞3 时，y 随 x 的增大而增大 10．（4 分）如图，四边形 ABCD 是边长为 1 的正方形，△BPC 是等边三角形，连接 DP 并延长交 CB 的延长线于点 H， 连接 BD 交 PC 于点 Q，下列结论： ① ∠BPD＝135°； ② △BDP∽△HDB； ③ DQ：BQ＝1：2； ④ S△BDP＝ ． 其中正确的有（ ） A． ①②③ B． ②③④ C． ①③④ D． ①②④二、填空题（本大题共 5 个小题，每小题 4 分，共 20 分） 11．（4 分）2018 年 10 月 24 日，我国又一项世界级工程﹣﹣港珠澳大桥正式建成通车，它全长 55000 米，用科学记数 法表示为 米． 12．（4 分）若关于 x 的方程 x2﹣2x+k＝0 有两个不相等的实数根，则 k 的取值范围为 ． 13．（4 分）某校拟招聘一批优秀教师，其中某位教师笔试、试讲、面试三轮测试得分分别为 92 分、85 分、90 分，综 合成绩笔试占 40%，试讲占 40%，面试占 20%，则该名教师的综合成绩为 分． 14．（4 分）阅读材料：定义：如果一个数的平方等于﹣1，记为 i2＝﹣1，这个数 i 叫做虚数单位，把形如 a+bi（a，b 为实数）的数叫做复数，其中 a 叫这个复数的实部，b 叫这个复数的虚部．它的加、减、乘法运算与整式的加、减、 乘法运算类似． 例如计算：（4+i）+（6﹣2i）＝（4+6）+（1﹣2）i＝10﹣i； （2﹣i）（3+i）＝6﹣3i+2i﹣i2＝6﹣i﹣（﹣1）＝7﹣i； （4+i）（4﹣i）＝16﹣i2＝16﹣（﹣1）＝17； （2+i）2＝4+4i+i2＝4+4i﹣1＝3+4i 根据以上信息，完成下面计算： （1+2i）（2﹣i）+（2﹣i）2＝ ． 15．（4 分）如图，在平面直角坐标系中，矩形 OABC 的顶点 O 落在坐标原点，点 A、点 C 分别位于 x 轴，y 轴的正半 轴，G 为线段 OA 上一点，将△OCG 沿 CG 翻折，O 点恰好落在对角线 AC 上的点 P 处，反比例函数 y＝ 经过点 B．二次函数 y＝ax2+bx+c（a≠0）的图象经过 C（0，3）、G、A 三点，则该二次函数的解析式为 ．（填一般 式） 三、计算或解答题（本大题共 10 小题，满分 90 分） 16．（7 分）计算：（﹣1）2019+（﹣2）﹣2+（3.14﹣ π ）0﹣4cos30°+|2﹣ | 17．（7 分）解不等式组： ，把它的解集在数轴上表示出来，并写出其整数解． 18．（7 分）先化简，再求值： ÷ ﹣ ，其中 a，b 满足（a﹣2）2+ ＝0． 19．（9 分）如图，在四边形 ABCD 中，AD∥BC，延长 BC 到 E，使 CE＝BC，连接 AE 交 CD 于点 F，点 F 是 CD 的 中点．求证： （1）△ADF≌△ECF． （2）四边形 ABCD 是平行四边形． 20．（9 分）汛期即将来临，为保证市民的生命和财产安全，市政府决定对一段长 200 米且横断面为梯形的大坝用土石 进行加固．如图，加固前大坝背水坡坡面从 A 至 B 共有 30 级阶梯，平均每级阶梯高 30cm，斜坡 AB 的坡度 i＝1：1； 加固后，坝顶宽度增加 2 米，斜坡 EF 的坡度 i＝1： ，问工程完工后，共需土石多少立方米？（计算土石方时忽 略阶梯，结果保留根号） 21．（9 分）仙桃是遂宁市某地的特色时令水果．仙桃一上市，水果店的老板用 2400 元购进一批仙桃，很快售完；老板 又用 3700 元购进第二批仙桃，所购件数是第一批的 倍，但进价比第一批每件多了 5 元． （1）第一批仙桃每件进价是多少元？ （2）老板以每件 225 元的价格销售第二批仙桃，售出 80%后，为了尽快售完，剩下的决定打折促销．要使得第二 批仙桃的销售利润不少于 440 元，剩余的仙桃每件售价至少打几折？（利润＝售价﹣进价） 22．（10 分）我市某校为了让学生的课余生活丰富多彩，开展了以下课外活动： 代号 活动类型 A 经典诵读与写作 B 数学兴趣与培优 C 英语阅读与写作 D 艺体类 E 其他 为了解学生的选择情况，现从该校随机抽取了部分学生进行问卷调查（参与问卷调查的每名学生只能选择其中一 项），并根据调查得到的数据绘制了如图所示的两幅不完整的统计图．请根据统计图提供的信息回答下列问题（要 求写出简要的解答过程）． （1）此次共调查了 名学生． （2）将条形统计图补充完整． （3）“数学兴趣与培优”所在扇形的圆心角的度数为 ． （4）若该校共有 2000 名学生，请估计该校喜欢 A、B、C 三类活动的学生共有多少人？ （5）学校将从喜欢“A”类活动的学生中选取 4 位同学（其中女生 2名，男生 2 名）参加校园“金话筒”朗诵初赛， 并最终确定两名同学参加决赛，请用列表或画树状图的方法，求出刚好一男一女参加决赛的概率． 23．（10 分）如图，一次函数 y＝x﹣3 的图象与反比例函数 y═ （k≠0）的图象交于点 A 与点 B（a，﹣4）． （1）求反比例函数的表达式； （2）若动点 P 是第一象限内双曲线上的点（不与点 A 重合），连接 OP，且过点 P 作 y 轴的平行线交直线 AB 于点 C， 连接 OC，若△POC 的面积为 3，求出点 P 的坐标． 24．（10 分）如图，△ABC 内接于 ⊙ O，直径 AD 交 BC 于点 E，延长 AD 至点 F，使 DF＝2OD，连接 FC 并延长交过 点 A 的切线于点 G，且满足 AG∥BC，连接 OC，若 cos∠BAC＝ ，BC＝6． （1）求证：∠COD＝∠BAC； （2）求 ⊙ O 的半径 OC； （3）求证：CF 是 ⊙ O 的切线． 25．（12分）如图，顶点为 P（3，3）的二次函数图象与 x 轴交于点 A（6，0），点 B 在该图象上，OB 交其对称轴 l 于 点 M，点 M、N 关于点 P 对称，连接 BN、ON． （1）求该二次函数的关系式． （2）若 点 B 在对称轴 l 右侧的二次函数图象上运动，请解答下列问题： ① 连接 OP，当 OP＝ MN 时，请判断△NOB 的形状，并求出此时点 B 的坐标． ② 求证：∠BNM＝∠ONM． 2019 年四川省遂宁市中考数学试卷 参考答案与试题解析 一、选择题（本大题共 10 个小题，每小题 4 分，共 40 分，在每个小题给出的四个选项中，只有一个符合题目要求.） 1．（4 分）﹣|﹣ |的值为（ ） A． B．﹣ C．± D．2 【分析】根据实数的绝对值的意义解答即可． 【解答】解：﹣|﹣ |＝﹣ ． 故选：B． 【点评】此题主要考查绝对值和二次根式，掌握实数的绝对值的意义是解题的关键． 2．（4 分）下列等式成立的是（ ） A．2+ ＝2 B．（a2b3）2＝a4b6 C．（2a2+a）÷a＝2a D．5x2y﹣2x2y＝3 【分析】直接利用整式的除法运算法则以及积的乘方运算法则、合并同类项法则、二次根式的加减运算法则分别化 简得出答案． 【解答】解：A、2+ ，无法计算，故此选项错误； B、（a2b3）2＝a4b6，正确； C、（2a2+a）÷a＝2a+1，故此选项错误； D、故 5x2y﹣2x2y＝3x2y，此选项错误； 故选：B． 【点评】此题主要考查了整式的除法运算以及积的乘方运算、合并同类项、二次根式的加减运算，正确掌握相关运 算法则是解题关键． 3．（4 分）如图为正方体的一种平面展开图，各面都标有数字，则数字为﹣2 的面与其对面上的数字 之积是（ ） A．﹣12 B．0 C．﹣8 D．﹣10[来源:学科网] 【分析】根据正方体的平面展开图的特征知，其相对面的两个正方形之间一定相隔一个正方形，所以数字为﹣2 的 面的对面上的数字是 6，其积为﹣12． 【解答】解：数字为﹣2 的面的对面上的数字是 6，其积为﹣2×6＝﹣12． 故选：A． 【点评】此题主要考查了正方体相对两个面上的文字，关键是掌握正方体展开图的特点． 4．（4 分）某校为了了解家长对“禁止学生带手机进入校园”这一规定的意见，随机对全校 100 名学生家长进行调查， 这一问题中样本是（ ） A．100 B．被抽取的 100 名学生家长 C．被抽取的 100 名学生家长的意见 D．全校学生家长的意见 【分析】总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，而 样本容量则是指样本中个体的数目．我们在区分总体、个体、样本、样本容量，这四个概念时，首先找出考查的对 象．从而找出总体、个体．再根据被收集数据的这一部分对象找出样本，最后再根据样本确定出样本容量． 【解答】解：某校为了了解家长对“禁止学生带手机进入校园”这一规定的意见，随机对全校 100 名学生家长进行 调查， 这一问题中样本是：被抽取的 100 名学生家长的意见． 故选：C． 【点评】此题考查了总体、个体、样本、样本容量，解题要分清具体问题中的总体、个体与样本，关键是明确考查 的对象．总体、个体与样本的考查对象是相同的，所不同的是范围的大小．样本容量是样本中包含的个体的数目， 不能带单位． 5．（4 分）已知关于 x 的一元二次方程（a﹣1）x2﹣2x+a2﹣1＝0 有一个根为 x＝0，则 a 的值为（ ） A．0 B．±1 C．1 D．﹣1 【分析】直接把 x＝0 代入进而方程，再结合 a﹣1≠0，进而得出答案． 【解答】解：∵关于 x 的一元二次方程（a﹣1）x2﹣2x+a2﹣1＝0 有一个根为 x＝0， ∴a2﹣1＝0，a﹣1≠0， 则 a 的值为：a＝﹣1． 故选：D． 【点评】此题主要考查了一元二次方程的解，注意二次项系数不能为零． 6．（4 分）如图，△ABC 内接于 ⊙ O，若∠A＝45°， ⊙ O 的半径 r＝4，则阴影部分的面积为（ ） A．4 π ﹣8 B．2 π C．4 π D．8 π ﹣8 【分析】根据圆周角定理得到∠BOC＝2∠A＝90°，根据扇形的面积和三角形的面积公式即可得到结论． 【解答】解：∵∠A＝45°， ∴∠BOC＝2∠A＝90°， ∴阴影部分的面积＝S 扇形 BOC﹣S△BOC＝ ﹣ ×4×4＝4 π ﹣8， 故选：A． 【点评】本题考查了三角形的外接圆与外心，圆周角定理，扇形的面积的计算，熟练掌握扇形的面积公式是解题的 关键． 7．（4 分）如图，▱ ABCD 中，对角线 AC、BD 相交于点 O，OE⊥BD 交 AD 于点 E，连接 BE， 若▱ ABCD 的周长为 28，则△ABE 的周长为（ ） A．28 B．24 C．21 D．14 【分析】先判断出 EO 是 BD 的中垂线，得出 BE＝ED，从而可得出△ABE 的周长＝AB+AD，再由平行四边形的周 长为 24，即可得出答案． 【解答】解：∵四边形 ABCD 是平行四边形， ∴OB＝OD，AB＝CD，AD＝BC， ∵平行四边形的周长为 28， ∴AB+AD＝14 ∵OE⊥BD， ∴OE 是线段 BD 的中垂线， ∴BE＝ED， ∴△ABE 的周长＝AB+BE+AE＝AB+AD＝14， 故选：D． 【点评】此题考查了平行四边形的性质及线段的中垂线的性质，解答本题的关键是判断出 OE 是线段 BD 的中垂线． 8．（4 分）关于 x 的方程 ﹣1＝ 的解为正数，则 k 的取值范围是（ ） A．k＞﹣4 B．k＜4 C．k＞﹣4 且 k≠4 D．k＜4 且 k≠﹣4 【分析】分式方程去分母转化为整式方程，求出整式的方程的解得到 x 的值，根据分式方程解是正数，即可确定出 k 的范围． 【解答】解：分式方程去分母得：k﹣（2x﹣4）＝2x， 解得：x＝ ， 根据题意得： ＞0，且 ≠2， 解得：k＞﹣4，且 k≠4． 故选：C． 【点评】此题考查了分式方程的解，本题需注意在任何时候都要考虑分母不为 0． 9．（4 分）二次函数 y＝x2﹣ax+b 的图象如图所示，对称轴为直线 x＝2，下列结论不正确的是（ ） A．a＝4 B．当 b＝﹣4 时，顶点的坐标为（2，﹣8） C．当 x＝﹣1 时，b＞﹣5 D．当 x＞3 时，y 随 x 的增大而增大 【分析】根据二次函数的图象和性质依次对各选项进行判断即可． 【解答】解：∵二次函数 y＝x2﹣ax+b ∴对称轴为直线 x＝ ＝2 ∴a＝4，故 A 选项正确； 当 b＝﹣4 时，y＝x2﹣4x﹣4＝（x﹣2）2﹣8 ∴顶点的坐标为（2，﹣8），故 B 选项正确； 当 x＝﹣1 时，由图象知此时 y＜0 即 1+4+b＜0 ∴b＜﹣5，故 C 选项不正确； ∵对称轴为直线 x＝2 且图象开口向上 ∴当 x＞3 时，y 随 x 的增大而增大，故 D 选项正确； 故选：C． 【点评】本题考查二次函数的图象与性质，解题的关键是熟练运用二次函数的图象与系数的关系，本题属于基础题 型． 10．（4 分）如图，四边形 ABCD 是边长为 1 的正方形，△BPC 是等边三角形，连接 DP 并延长交 CB 的延长线于点 H， 连接 BD 交 PC 于点 Q，下列结论： ① ∠BPD＝135°； ② △BDP∽△HDB； ③ DQ：BQ＝1：2； ④ S△BDP＝ ． 其中正确的有（ ） A． ①②③ B． ②③④ C． ①③④ D． ①②④ [ 来源 :Zxxk.Com] 【分析】由等边三角形及正方形的性质求出∠CPD＝∠CDP＝75°、∠PCB＝∠CPB＝60°，从而判断 ① ；证∠DBP ＝∠DPB＝135°可判断 ② ；作 QE⊥CD，设 QE＝DE＝x，则 QD＝ x，CQ＝2QE＝2x，CE＝ x，由 CE+DE ＝CD 求出 x，从而求得 DQ、BQ 的长，据此可判断 ③ ，证 DP＝DQ＝ ，根据 S△BDP＝ BD•PDsin∠BDP 求解可判断 ④ ． 【解答】解：∵△PBC 是等边三角形，四边形 ABCD 是正方形， ∴∠PCB＝∠CPB＝60°，∠PCD＝30°，BC＝PC＝CD， ∴∠CPD＝∠CDP＝75°， 则∠BPD＝∠BPC+∠CPD＝135°，故 ① 正确； ∵∠CBD＝∠CDB＝45°， ∴∠DBP＝∠DPB＝135°， 又∵∠PDB＝∠BDH， ∴△BDP∽△HDB，故 ② 正确； 如图，过点 Q 作 QE⊥CD 于 E， 设 QE＝DE＝x，则 QD＝ x，CQ＝2QE＝2x， ∴CE＝ x， 由 CE+DE＝CD 知 x+ x＝1， 解得 x＝ ， ∴QD＝ x＝ ， ∵BD＝ ， ∴BQ＝BD﹣DQ＝ ﹣ ＝ ， 则 DQ：BQ＝ ： ≠1：2，故 ③ 错误； ∵∠CDP＝75°，∠CDQ＝45°， ∴∠PDQ＝30°， 又∵∠CPD＝75°， ∴∠DPQ＝∠DQP＝75°， ∴DP＝DQ＝ ， ∴S△BDP＝ BD•PDsin∠BDP＝ × × × ＝ ，故 ④ 正确； 故选：D． 【点评】本题主要考查相似三角形的判定与性质，解题的关键是熟练掌握等边三角形和正方形的性质、等腰三角形 的判定与性质及相似三角形的判定等知识点． 二、填空题（本大题共 5 个小题，每小题 4 分，共 20 分） 11．（4 分）2018 年 10 月 24 日，我国又一项世界级工程﹣﹣港珠澳大桥正式建成通车，它全长 55000 米，用科学记数 法表示为 5.5×104 米． 【分析】科学记数法的表示形式为 a×10n 的形式，其中 1≤|a|＜10，n 为整数．确定 n 的值是易错点，由于 55000 有 5 位，所以可以确定 n＝5﹣1＝4． 【解答】解：55000＝5.5×104， 故答案为 5.5×104． 【点评】此题考查科学记数法表示较大的数的方法，准确确定 a 与 n 值是关键． 12．（4 分）若关于 x 的方程 x2﹣2x+k＝0 有两个不相等的实数根，则 k 的取值范围为 k＜1 ． 【分析】利用根的判别式进行计算，令△＞0 即可得到关于 k 的不等式，解答即可． 【解答】解：∵关于 x 的方程 x2﹣2x+k＝0 有两个不相等的实数根， ∴△＞0， 即 4﹣4k＞0， k＜1． 故答案为：k＜1． 【点评】本题考查了根的判别式，要知道一元二次方程根的情况与判别式△的关系： （1）△＞0 ⇔ 方程有两个不相等的实数根； （2）△＝0 ⇔ 方程有两个相等的实数根； （3）△＜0 ⇔ 方程没有实数根． 13．（4 分）某校拟招聘一批优秀教师，其中某位教师笔试、试讲、面试三轮测试得分分别为 92 分、85 分、90 分，综 合成绩笔试占 40%，试讲占 40%，面试占 20%，则该名教师的综合成绩为 88.8 分． 【分析】根据加权平均数的计算方法求值即可． 【解答】解：由题意，则该名教师的综合成绩为： 92×40%+85×40%+90×20% ＝36.8+34+18 ＝88.8 故答案为：88.8 【点评】本题考查了加权平均数．掌握加权平均数的算法是解决本题的关键． 14．（4 分）阅读材料：定义：如果一个数的平方等于﹣1，记为 i2＝﹣1，这个数 i 叫做虚数单位，把形如 a+bi（a，b 为实数）的数叫做复数，其中 a 叫这个复数的实部，b 叫这个复数的虚部．它的加、减、乘法运算与整式的加、减、 乘法运算类似． 例如计算：（4+i）+（6﹣2i）＝（4+6）+（1﹣2）i＝10﹣i； （2﹣i）（3+i）＝6﹣3i+2i﹣i2＝6﹣i﹣（﹣1）＝7﹣i； （4+i）（4﹣i）＝16﹣i2＝16﹣（﹣1）＝17； （2+i）2＝4+4i+i2＝4+4i﹣1＝3+4i 根据以上信息，完成下面计算： （1+2i）（2﹣i）+（2﹣i）2＝ 7﹣i ． 【分析】直接利用完全平方公式以及多项式乘法分别化简得出答案． 【解答】解：（1+2i）（2﹣i）+（2﹣i）2＝2﹣i+4i﹣2i2+4+i2﹣4i ＝6﹣i﹣i2 ＝6﹣i+1 ＝7﹣i． 故答案为：7﹣i． 【点评】此题主要考查了实数运算，正确运用相关计算法则是解题关键． 15．（4 分）如图，在平面直角坐标系中，矩形 OABC 的顶点 O 落在坐标原点，点 A、点 C 分别位于 x 轴，y 轴的正半 轴，G 为线段 OA 上一点，将△OCG 沿 CG 翻折，O 点恰好落在对角线 AC 上的点 P 处，反比例函数 y＝ 经 过点 B．二次函数 y＝ax2+bx+c（a≠0）的图象经过 C（0，3）、G、A 三点，则该二次函数的解析式为 y＝ x2﹣ x+3 ．（填 一般式） 【分析】点 C（0，3），反比例函数 y＝ 经过点 B，则点 B（4，3），由勾股定理得：（4﹣x）2＝4+x2，故点 G（ ， 0），将点 C、G、A 坐标代入二次函数表达式，即可求解． 【解答】解：点 C（0，3），反比例函数 y＝ 经过点 B，则点 B（4，3）， 则 OC＝3，OA＝4， ∴AC＝5， 设 OG＝PG＝x，则 GA＝4﹣x，PA＝AC﹣CP＝AC﹣OC＝5﹣3＝2， 由勾股定理得：（4﹣x）2＝4+x2， 解得：x＝ ，故点 G（ ，0）， 将点 C、G、A 坐标代入二次函数表达式得： ，解得： ， 故答案为：y＝ x2﹣ x+3． 【点评】本题考查的是二次函数综合运用，涉及到矩形基本性质、反比例函数基本性质与应用，其中用勾股定理求 OG 的长度，是本题解题的关键． 三、计算或解答题（本大题共 10 小题，满分 90 分） 16．（7 分）计算：（﹣1）2019+（﹣2）﹣2+（3.14﹣ π ）0﹣4cos30°+|2﹣ | 【分析】直接利用负指数幂的性质以及特殊角的三角函数值、绝对值的性质分别化简得出答案． 【解答】解：原式＝﹣1+ +1﹣4× +2 ﹣2 ＝﹣1+ +1﹣2 +2 ﹣2 ＝﹣ ． 【点评】此题主要考查了实数运算，正确化简各数是解题关键． 17．（7 分）解不等式组： ，把它的解集在数轴上表示出来，并写出其整数解． 【分析】一元一次不等式组的解法：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的 公共部分，利用数轴可以直观地表示不等式组的解集． 方法与步骤： ① 求不等式组中每个不等式的解集； ② 利用数轴求公共部分．解集的规律：同大取大；同小取小；大 小小大中间找；大大小小找不到． 【解答】解： 解不等式 ① ，x＞﹣3， 解不等式 ② ，x≤2， ∴﹣3＜x≤2， 解集在数轴上表示如下： ∴x 的整数解为﹣2，﹣1，0，1，2． 【点评】本题考查了不等式的解集，正确理解数轴上不等式解集的意义是解题的关键． 18．（7 分）先化简，再求值： ÷ ﹣ ，其中 a，b 满足（a﹣2）2+ ＝0． 【分析】先化简分式，然后将 a、b 的值代入计算即可． 【解答】解：原式＝ ﹣ ＝ ﹣ ＝﹣ ， ∵a，b 满足（a﹣2）2+ ＝0， ∴a﹣2＝0，b+1＝0， a＝2，b＝﹣1， 原式＝ ＝﹣1． 【点评】本题考查了分式的化简求值，熟练掌握分式混合运算法则是解题的关键． 19．（9 分）如图，在四边形 ABCD 中，AD∥BC，延长 BC 到 E，使 CE＝BC，连接 AE 交 CD 于点 F，点 F 是 CD 的 中点．求证： （1）△ADF≌△ECF． （2）四边形 ABCD 是平行四边形． 【分析】（1）根据平行线的性质得到∠DAF＝∠E，根据线段中点的定义得到 DF＝CF，根据全等三角形的判定定理 即可得到结论； （2）根据全等三角形的性质得到 AD＝EC，等量代换得到 AD＝BC，根据平行四边形的判定定理即可得到结论． 【解答】证明：（1）∵AD∥BC， ∴∠DAF＝∠E， ∵点 F 是 CD 的中点， ∴DF＝CF， 在△ADF 与△ECF 中， ， ∴△ADF≌△ECF（AAS）； （2）∵△ADF≌△ECF， ∴AD＝EC， ∵CE＝BC， ∴AD＝BC， ∵AD∥BC，[来源:学科网] ∴四边形 ABCD 是平行四边形． 【点评】本题考查了平行四边形的判定和性质，全等三角形的判定和性质，熟练掌握平行双绞线的判定定理是解题 的关键． 20．（9 分）汛期即将来临，为保证市民的生命和财产安全，市政府决定对一段长 200 米且横断面为梯形的大坝用土石 进行加固．如图，加固前大坝背水坡坡面从 A 至 B 共有 30 级阶梯，平均每级阶梯高 30cm，斜坡 AB 的坡度 i＝1：1； 加固后，坝顶宽度增加 2 米，斜坡 EF 的坡度 i＝1： ，问工程完工后，共需土石多少立方米？（计算土石方时忽 略阶梯，结果保留根号） 【分析】过 A 作 AH⊥BC 于 H，过 E 作 EH⊥BC 于 G，于是得到四边形 EGHA 是矩形，求得 EG＝AH，GH＝AE ＝2，得到 AH＝BH＝ ，求得 BG＝BH﹣HG＝ ，得到 FG＝ ，根据梯形的面积公式求得梯形 ABFE 的面积乘以大坝的长度即可得到结论． 【解答】解：过 A 作 AH⊥BC 于 H，过 E 作 EH⊥BC 于 G， 则四边形 EGHA 是矩形， ∴EG＝AH，GH＝AE＝2， ∵AB＝30×30＝900cm＝9 米， ∵斜坡 AB 的坡度 i＝1：1， ∴AH＝BH＝ ， ∴BG＝BH﹣HG＝ ， ∵斜坡 EF的坡度 i＝1： ， ∴FG＝ ， ∴BF＝FG﹣BG＝ ﹣ ， ∴S 梯形 ABFE＝ （2+ ﹣ ）× ＝ ， ∴共需土石为 ×200＝50（81 ﹣81+36 ）立方米． 【点评】此题考查了坡度坡角问题．此题难度适中，注意构造直角三角形，并借助于解直角三角形的知识求解是关 键． 21．（9 分）仙桃是遂宁市某地的特色时令水果．仙桃一上市，水果店的老板用 2400 元购进一批仙桃，很快售完；老板 又用 3700 元购进第二批仙桃，所购件数是第一批的 倍，但进价比第一批每件多了 5 元． （1）第一批仙桃每件进价是多少元？ （2）老板以每件 225 元的价格销售第二批仙桃，售出 80%后，为了尽快售完，剩下的决定打折促销．要使得第二 批仙桃的销售利润不少于 440 元，剩余的仙桃每件售价至少打几折？（利润＝售价﹣进价） 【分析】（1）设第一批仙桃每件进价是 x 元，则第二批每件进价是（x+5）元，再根据等量关系：第二批仙桃所购件 数是第一批的 倍，列方程解答； （2）设剩余的仙桃每件售价 y 元，由利润＝售价﹣进价，根据第二批的销售利润不低于 440 元，可列不等式求解． 【解答】解：（1）设第一批仙桃每件进价 x 元，则 × ＝ ， 解得 x＝180． 经检验，x＝180 是原方程的根． 答：第一批仙桃每件进价为 180 元； （2）设剩余的仙桃每件售价打 y 折．[来源:学科网 ZXXK] 则： ×225×80%+ ×225×（1﹣80%）×0.1y﹣3700≥440， 解得 y≥6． 答：剩余的仙桃每件售价至少打 6 折． 【点评】本题考查分式方程、一元一次不等式的应用，关键是根据数量作为等量关系列出方程，根据利润作为不等 关系列出不等式求解． 22．（10 分）我市某校为了让学生的课余生活丰富多彩，开展了以下课外活动： 代号 活动类型 A 经典诵读与写作 B 数学兴趣与培优 C 英语阅读与写作 D 艺体类 E 其他 为了解学生的选择情况，现从该校随机抽取了部分学生进行问卷调查（参与问卷调查的每名学生只能选择其中一 项），并根据调查得到的数据绘制了如图所示的两幅不完整的统计图．请根据统计图提供的信息回答下列问题（要 求写出简要的解答过程）． （1）此次共调查了 200 名学生． （2）将条形统计图补充完整． （3）“数学兴趣与培优”所在扇形的圆心角的度数为 108° ． （4）若该校共有 2000 名学生，请估计该校喜欢 A、B、C 三类活动的学生共有多少人？ （5）学校将从喜欢“A”类活动的学生中选取 4 位同学（其中女生 2 名，男生 2 名）参加校园“金话筒”朗诵初赛， 并最终确定两名同学参加决赛，请用列表或画树状图的方法，求出刚好一男一女参加决赛的概率． 【分析】（1）由 A 类型人数及其所占百分比可得总人数； （2）总人数乘以 D 的百分比求得其人数，再根据各类型人数之和等于总人数求得 B 的人数，据此可补全图形； （3）用 360°乘以 B 类型人数所占比例； （4）总人数乘以前三项人数之和所占比例即可得； （5）首先根据题意画出树状图，然后由树状图即可求得所有等可能的结果与挑选的两位学生恰好是一男一女的情 况，再利用概率公式求解即可求得答案 【解答】解：（1）此次调查的总人数为 40÷20%＝200（人）， 故答案为：200； （2）D 类型人数为 200×25%＝50（人）， B 类型人数为 200﹣（40+30+50+20）＝60（人）， 补全图形如下： （3）“数学兴趣与培优”所在扇形的圆心角的度数为 360°× ＝108°， 故答案为：108°； （4）估计该校喜欢 A、B、C 三类活动的学生共有 2000× ＝1300（人）； （5）画树状图如下： ， 由树状图知，共有 12 种等可能结果，其中一男一女的有 8 种结果， ∴刚好一男一女参加决赛的概率 ＝ ． 【点评】此题考查了列表法或树状图法求概率、频数分布直方图、扇形统计图．用到的知识点为：概率＝所求情况 数与总情况数之比． 23．（10 分）如图，一次函数 y＝x﹣3 的图象与反比例函数 y═ （k≠0）的图象交于点 A 与点 B（a，﹣4）． （1）求反比例函数的表达式； （2）若动点 P 是第一象限内双曲线上的点（不与点 A 重合），连接 OP，且过点 P 作 y 轴的平行线交直线 AB 于点 C， 连接 OC，若△POC 的面积为 3，求出点 P 的坐标． 【分析】（1）先求出点 B 的坐标，然后利用待定系数法将 B 代入反比例函数解析式中即可求出其表达式； （2）设点 P 的坐标为（m， ）（m＞0），用 m 表示出△POC 的面积，从而列出关于 m 的方程，解方程即可． 【解答】解：（1）将 B（a，﹣4）代入一次函数 y＝x﹣3 中得：a＝﹣1 ∴B（﹣1，﹣4） 将 B（﹣1，﹣4）代入反比例函数 y═ （k≠0）中得：k＝4 ∴反比例函数的表达式为 y＝ ； （2）如图： 设点 P 的坐标为（m， ）（m＞0），则 C（m，m﹣3） ∴PC＝| ﹣（m﹣3）|，点 O 到直线 PC 的距离为 m ∴△POC 的面积＝ m×| ﹣（m﹣3）|＝3 解得：m＝5 或﹣2 或 1 或 2 ∵点 P 不与点 A 重合，且 A（4，1） ∴m≠4 又∵m＞0 ∴m＝5 或 1 或 2 ∴点 P 的坐标为（5， ）或（1，4）或（2，2）． 【点评】本题主要考查了反比例函数与一次函数的交点问题，待定系数法求反比例函数的表达式，一次函数图象上 点的坐标特征，三角形面积．本题属于中考常考题型． 24．（10 分）如图，△ABC 内接于 ⊙ O，直径 AD 交 BC 于点 E，延长 AD 至点 F，使 DF＝2OD，连接 FC 并延长交过 点 A 的切线于点 G，且满足 AG∥BC，连接 OC，若 cos∠BAC＝ ，BC＝6． （1）求证：∠COD＝∠BAC； （2）求 ⊙ O 的半径 OC； （3）求证：CF 是 ⊙ O 的切线． 【分析】（1）根据切线的性质得到∠GAF＝90°，根据平行线的性质得到 AE⊥BC，根据圆周角定理即可得到结论； （2）设 OE＝x，OC＝3x，得到 CE＝3，根据勾股定理即可得到结论； （3）由 DF＝2OD，得到 OF＝3OD＝3OC ，求得 ，推出△COE∽△FOE，根据相似三角形的性质得到 ∠OCF＝∠DEC＝90°，于是得到 CF 是 ⊙ O 的切线． 【解答】解：（1）∵AG 是 ⊙ O 的切线，AD 是 ⊙ O 的直径， ∴∠GAF＝90°， ∵AG∥BC， ∴AE⊥BC， ∴CE＝BE， ∴∠BAC＝2∠EAC，[来源:学科网 ZXXK] ∵∠COE＝2∠CAE， ∴∠COD＝∠BAC； （2）∵∠COD＝∠BAC， ∴cos∠BAC＝cos∠COE＝ ＝ ， ∴设 OE＝x，OC＝3x， ∵BC＝6， ∴CE＝3， ∵CE⊥AD， ∴OE2+CE2＝OC2， ∴x2+32＝9x2， ∴x＝ （负值舍去）， ∴OC＝3x＝ ， ∴ ⊙ O 的半径 OC 为 ； （3）∵DF＝2OD， ∴OF＝3OD＝3OC， ∴ ， ∵∠COE＝∠FOC， ∴△COE∽△FOE， ∴∠OCF＝∠DEC＝90°， ∴CF 是 ⊙ O 的切线． 【点评】本题考查了切线的判定和性质，相似三角形的判定和性质，解直角三角形，平行线的性质，正确的识别图 形是解题的关键． 25．（12 分）如图，顶点为 P（3，3）的二次函数图象与 x 轴交于点 A（6，0），点 B 在该图象上，OB 交其对称轴 l 于 点 M，点 M、N 关于点 P 对称，连接 BN、ON． （1）求该二次函数的关系式． （2）若点 B 在对称轴 l 右侧的二次函数图象上运动，请解答下列问题： ① 连接 OP，当 OP＝ MN 时，请判断△NOB 的形状，并求出此时点 B 的坐标． ② 求证：∠BNM＝∠ONM． 【分析】（1）由于已知二次函数顶点坐标，故可设顶点式，再把点 A 代入求 a 即求得二次函数关系式． （2）设点 B 横坐标为 b，用 b 表示直线 OB 的 k 值即得到直线 OB 解析式，把 x＝3 代入即用 b 表示点 M 坐标．根 据 M、N 关于点 P 对称，求得 MP＝NP＝ MN，且能用 b 表示点 N 坐标． ① 由 OP＝ MN，可列得关于 b 的方程， 求解即得到点 B、N 坐标．求 OB2、ON2、BN2 的值得到 OB2+ON2＝BN2，判断△NOB 是等腰直角三角形． ② 有点 B、 N 坐标求直线 BN 解析式（含 b），令 y＝0 求得直线 BN 与 x 轴交点 D 的坐标，发现 C 为 OD 中点即直线 NC 垂直平 分 OD，根据垂直平分线性质得 ND＝NO，由等腰三角形三线合一得∠BNM＝∠ONM，得证． 【解答】解：（1）∵二次函数顶点为 P（3，3） ∴设顶点式 y＝a（x﹣3）2+3 ∵二次函数图象过点 A（6，0） ∴（6﹣3）2a+3＝0，解得：a＝﹣ ∴二次函数的关系式为 y＝﹣ （x﹣3）2+3＝﹣ x2+2x （2）设 B（b，﹣ b2+2b）（b＞3） ∴直线 OB 解析式为：y＝（﹣ b+2）x ∵OB 交对称轴 l 于点 M ∴当 xM＝3 时，yM＝（﹣ b+2）×3＝﹣b+6 ∴M（3，﹣b+6） ∵点 M、N 关于点 P 对称 ∴NP＝MP＝3﹣（﹣b+6）＝b﹣3， ∴yN＝3+b﹣3＝b，即 N（3，b） ① ∵OP＝ MN ∴OP＝MP ∴ ＝b﹣3 解得：b＝3+3 ∴﹣ b2+2b＝﹣ ×（3+3 ）2+2×（3+3 ）＝﹣3 ∴B（3+3 ，﹣3），N（3，3+3 ） ∴OB2＝（3+3 ）2+（﹣3）2＝36+18 ，ON2＝32+（3+3 ）2＝36+18 ，BN2＝（3+3 ﹣3）2+（﹣3﹣3﹣ 3 ）2＝72+36 ∴OB＝ON，OB2+ON2＝BN2 ∴△NOB 是等腰直角三角形，此时点 B 坐标为（3+3 ，﹣3）． ② 证明：如图，设直线 BN 与 x 轴交于点 D ∵B（b，﹣ b2+2b）、N（3，b） 设直线 BN 解析式为 y＝kx+d ∴ 解得： ∴直线 BN：y＝﹣ bx+2b 当 y＝0 时，﹣ bx+2b＝0，解得：x＝6 ∴D（6，0） ∵C（3，0），NC⊥x 轴 ∴NC 垂直平分 OD ∴ND＝NO ∴∠BNM＝∠ONM 【点评】本题考查了二次函数的图象与性质，一次函数的图象与性质，对称的性质，勾股定理逆定理，一元一次方 程的解法，垂直平分线的判定和性质，等腰三角形的性质．第（2）题设点 B 横坐标为 b 后，即把 b 当常数进行求 直线解析式和点坐标的运算，较多字母的运算过程要抓清楚常量和变量． 声明：试 题解析著作权 属菁优网所有 ，未经书面同 意，不得复制 发布 日期： 2019/6/26 18:03:01；用户： 冯锡眉；邮箱 ：zxfengxm@xyh.com ；学号： 22634181