九年级数学下册第一章直角三角形的边角关系阶段专题复习习题课件北师大版 33页

阶段专题复习 第 一 章 ①__________________________________________________ _______________________________ ②__________________________________________________ _______________________________ ③__________________________________________________ _______________________________ 在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比 也随之确定,这个比叫做∠A的正切 在Rt△ABC中,如果锐角A确定,那么∠A的对边与斜边的比 也随之确定,这个比叫做∠A的正弦 在Rt△ABC中,如果锐角A确定,那么∠A的邻边与斜边的比 也随之确定,这个比叫做∠A的余弦 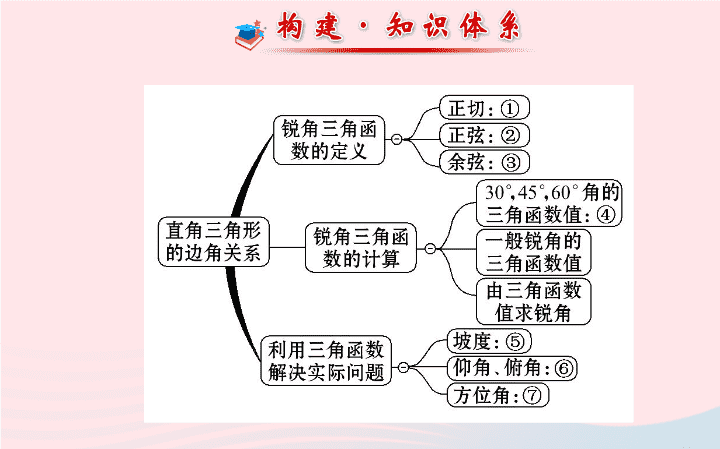请写出框图中数字处的内容： ④_______________________________________________ _____________________________________________________ ⑤___________________________________________________ ⑥___________________________________________________ ____________________________________________ ⑦__________________________________________________ _________ 坡面的铅直高度与水平宽度的比叫做坡面的坡度(或坡比) 在进行测量时,视线与水平线所成角中,规定：视线在水平 线上方的叫做仰角,视线在水平线下方的叫做俯角 指北或指南方向线与目标方向线所成的小于90°的角,叫 做方位角 考点 1 锐角三角函数 【知识点睛】 1.锐角三角函数包括以下三种函数 (1)正弦.(2)余弦.(3)正切. 2.锐角三角函数的取值范围 (1)锐角的三角函数值都是正数，而且没有单位. (2)00. 3.锐角三角函数的增减性 (1)正弦值、正切值随着角度的增大而增大. (2)余弦值随着角度的增大而减小. 【例1】(2012·泰州中考)如图，在边长相同的小正方形组成 的网格中，点A,B,C,D都在这些小正方形的顶点上，AB , CD相 交于点P，则tan∠APD的值是______． 【思路点拨】连接AE,BE,由勾股定理算出AE,BE,AB的长,由 ∠ABE=∠APD,∠AEB=90°,确定tan∠ABE的值,即为tan∠APD 的值. 【自主解答】连接AE,BE，设小正方形的边长为1，由勾股定 理得， ∴AB2=AE2+BE2,∴∠AEB=90°， ∵BE∥CD，∴∠ABE =∠APD， ∴tan∠APD=tan∠ABE=2. 答案：2 【中考集训】 1.(2012·包头中考)在Rt△ABC中，∠C=90°，若AB=2AC，则 sin A的值是( ) 【解析】选C．设AC=k，则AB=2k， 2.(2013·鄂州中考)如图，Rt△ABC中，∠A＝90°，AD⊥BC 于点D，若BD∶CD＝3∶2,则tan B=( ) 【解析】选D.由题意可知∠ADB＝∠CDA＝90°， ∠B＝∠DAC，∴△ABD∽△CAD, ∵BD∶CD=3∶2,设BD＝3x,则CD＝2x, 3.(2012·赤峰中考)如图，直线l1：y=x与双曲线 相交于 点A(a，2)，将直线l1向上平移3个单位得到l2，直线l2与双曲线 相交于B,C两点(点B在第一象限)，交y轴于D点． (1)求双曲线 的表达式. (2)求tan∠DOB的值． 【解析】(1)∵A(a，2)是y=x与 的交点，∴A(2，2)， 把A(2，2)代入 得k=4， ∴双曲线的表达式为 (2)∵将l1向上平移了3个单位得到l2， ∴l2的表达式为y=x+3， ∴解方程组 考点 2 特殊角的三角函数值 【知识点睛】 特殊角的三角函数值 锐角α 三角函数 30° 45° 60° sinα cosα tanα 1 【例2】(2012·梅州中考)计算： 【思路点拨】根据绝对值的性质、二次根式的运算法则、特殊 角的三角函数值及负整数指数幂计算出各数，再根据实数混合 运算的法则进行计算即可． 【自主解答】原式 【中考集训】 1.(2013·天津中考)tan 60°等于( ) 【解析】选C. 2.(2013·大庆中考)计算：sin2 60°+cos 60°-tan 45° =______． 【解析】原式 答案： 3.(2012·孝感中考)计算：cos245°+tan 30°·sin 60° =______. 【解析】 答案：1 4.(2013·扬州中考)计算： 【解析】原式 考点 3 直角三角形边角关系的应用 【知识点睛】 直角三角形边角关系应用的“四思想” 1.数形结合思想：通过画图来辅助解决问题. 2.转化思想：把实际问题转化为数学问题,把非直角三角形转 化为直角三角形来求解. 3.方程思想：依据三角函数构建相应的方程求解. 4.数学建模思想：建立直角三角形边角关系模型表示实际问题 中的数量关系. 【例3】(2012·湛江中考)某兴趣小组用仪器测量湛江海湾大 桥主塔的高度.如图，在距主塔AE 60 m的D处， 用仪器测得主塔顶部A的仰角为68°，已知测量 仪器的高CD＝1.3 m，求主塔AE的高度(结果精 确到0.1 m). (参考数据：sin 68°≈0.93，cos 68°≈0.37， tan 68°≈2.48) 【思路点拨】在Rt△ABC中，先根据AB=BC·tan 68°求出AB， 再由BE=CD，即可求得主塔AE的高度． 【自主解答】BE＝CD=1.3 m，BC＝DE=60 m. 在Rt△ACB中， 即AB＝60×tan 68°.∴AB≈148.8. ∴AE＝AB＋BE＝148.8＋1.3＝150.1(m). 答：主塔AE的高度约为150.1 m. 【中考集训】 1.(2013·山西中考)如图，某地修建高速公路，要从B地向C 地修一座隧道(B，C在同一水平面上)，为了测量B，C两地之 间的距离，某工程师乘坐热气球从C地出发，垂直上升100 m 到达A处，在A处观察B地的俯角为30°，则B，C两地之间的距 离为( ) 【解析】选A.根据在A处观察B地的俯角为30°，可得∠B=30° ，在Rt△ABC中， 所以 (m),故选A. 2.(2013·上海中考)某地下车库出口处“两段式栏杆”如图1 所示,点A是栏杆转动的支点,点E是栏杆两段的连接点.当车辆 经过时,栏杆AEF升起后的位置如图2所示,其示意图如图3所示, 其中AB⊥BC,EF∥BC,∠EAB=143°,AB=AE=1.2米,求当车辆经过 时,栏杆EF段距离地面的高度(即直线EF上任意一点到直线BC的 距离). (结果精确到0.1米,栏杆宽度忽略不计,参考数据: sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) 【解析】过点A作AH∥BC，EH⊥AH， ∵∠EAB=143°，∴∠EAH＝53°，∠AEH＝37°, ∵AE＝1.2，∴EH≈AE·0.80＝0.96(米). 所以栏杆EF距离地面的高度是0.96+1.2＝2.16≈2.2(米). 3.(2012·桂林中考)某市正在 进行商业街改造，商业街起点 在古民居P的南偏西60度方向 上的A处，现已改造至古民居P 的南偏西30度方向上的B处，A与B相距150 m.且B在A的正东方 向，为了不破坏古民居的风貌，按有关规定，在古民居的周围 100 m内不得修建现代化商业街，若工程队继续向正东方向修 建200 m商业街到C处，则对于从B到C的商业街改造是否违反有 关规定？ 【解析】如图，过点P作PM垂直BC于点M，∵∠APM＝60°， ∠BPM＝30°，∠AMP＝90°， ∴∠A＝30°，∠APB＝30°， ∴∠A＝∠APB， ∴BP＝AB＝150， 在Rt△BPM中，PM=BPcos∠BPM 所以从B到C的商业街改造不违反有关规定. 【归纳整合】利用直角三角形的边角关系解决实际问题时，常 遇到双直角三角形问题.双直角三角形通常是指两个直角三角 形一条直角边重合，另一条直角边共线.解题时常用公共边或 相等的直角边沟通已知条件和未知元素之间的关系，设定未知 数找出等量关系列出方程，从而求出结果. 4.(2013·兰州中考)如图，在活动课上， 小明和小红合作用一副三角板来测量学 校旗杆高度．已知小明的眼睛与地面的 距离(AB)是1.7 m，他调整自己的位置，设法使得三角板的一 条直角边保持水平，且斜边与旗杆顶端M在同一条直线上，测 得旗杆顶端M仰角为45°；小红的眼睛与地面的距离(CD)是 1.5 m，用同样的方法测得旗杆顶端M的仰角为30°．两人相距 28米且位于旗杆两侧(点B，N，D在同一条直线上)．求出旗杆 MN的高度．(参考数据： 结果保留整数) 【解析】过点A作AE⊥MN于E，过点C作CF⊥MN于F， 则EF=AB－CD=1.7－1.5=0.2(米). 在Rt△AEM中，∵∠MAE=45°，∴AE=ME. 设AE=ME=x，∴MF=x＋0.2. 在Rt△MFC中，∠MCF=30°， 因为AE+CF=28，所以 ∴x≈10，∴MN≈12. 答：旗杆高约为12米.