2019年浙江省丽水市中考数学试卷含答案 30页

‎2019年浙江省丽水市中考数学试卷 一、选择题（本题有10小题，每小题3分，共30分）.‎ ‎1．（3分）实数4的相反数是（　　）‎ A．‎-‎‎1‎‎4‎ B．﹣4 C．‎1‎‎4‎ D．4‎ ‎2．（3分）计算a6÷a3，正确的结果是（　　）‎ A．2 B．3a C．a2 D．a3‎ ‎3．（3分）若长度分别为a，3，5的三条线段能组成一个三角形，则a的值可以是（　　）‎ A．1 B．2 C．3 D．8‎ ‎4．（3分）某地一周前四天每天的最高气温与最低气温如表，则这四天中温差最大的是（　　）‎ 星期 一 二 三 四 最高气温 ‎10°C ‎12°C ‎11°C ‎9°C 最低气温 ‎3°C ‎0°C ‎﹣2°C ‎﹣3°C A．星期一 B．星期二 C．星期三 D．星期四 ‎5．（3分）一个布袋里装有2个红球、3个黄球和5个白球，除颜色外其它都相同．搅匀后任意摸出一个球，是白球的概率为（　　）‎ A．‎1‎‎2‎ B．‎3‎‎10‎ C．‎1‎‎5‎ D．‎‎7‎‎10‎ ‎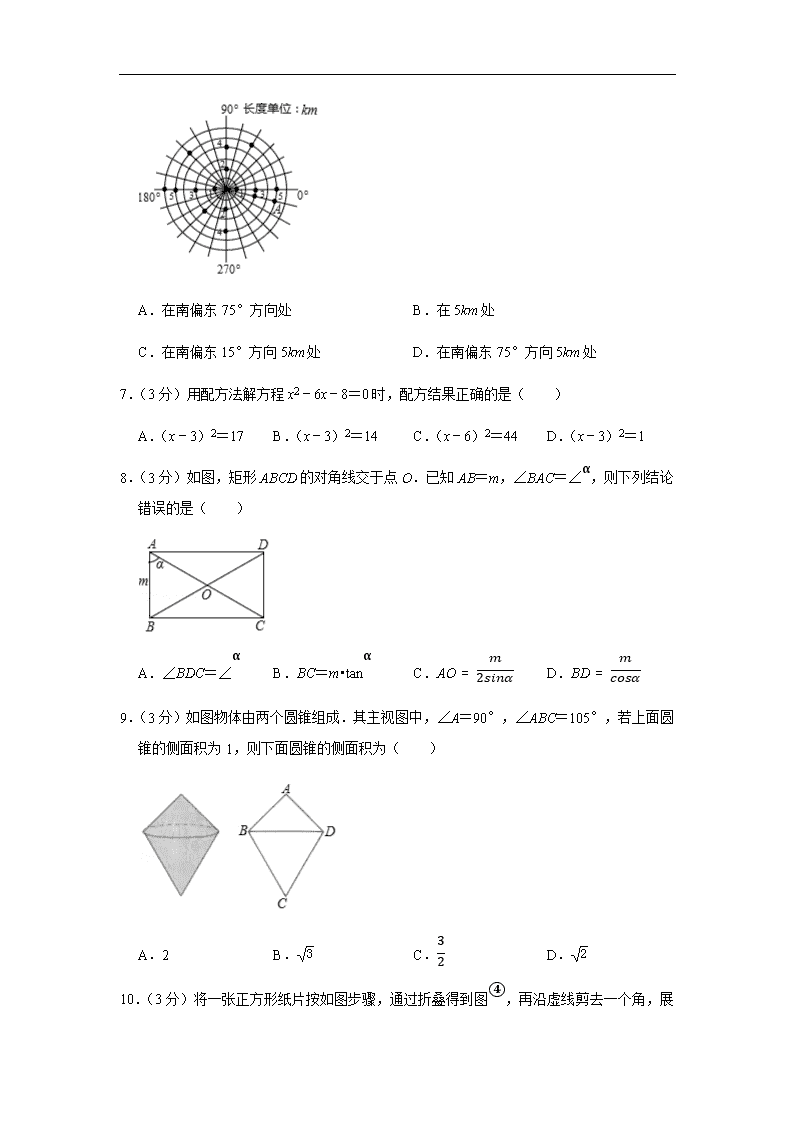6．（3分）如图是雷达屏幕在一次探测中发现的多个目标，其中对目标A的位置表述正确的是（　　）‎ A．在南偏东75°方向处 B．在5km处 ‎ C．在南偏东15°方向5km处 D．在南偏东75°方向5km处 ‎7．（3分）用配方法解方程x2﹣6x﹣8＝0时，配方结果正确的是（　　）‎ A．（x﹣3）2＝17 B．（x﹣3）2＝14 C．（x﹣6）2＝44 D．（x﹣3）2＝1‎ ‎8．（3分）如图，矩形ABCD的对角线交于点O．已知AB＝m，∠BAC＝∠α，则下列结论错误的是（　　）‎ A．∠BDC＝∠α B．BC＝m•tanα C．AO‎=‎m‎2sinα D．BD‎=‎mcosα ‎9．（3分）如图物体由两个圆锥组成．其主视图中，∠A＝90°，∠ABC＝105°，若上面圆锥的侧面积为1，则下面圆锥的侧面积为（　　）‎ A．2 B．‎3‎ C．‎3‎‎2‎ D．‎‎2‎ ‎10．（3分）将一张正方形纸片按如图步骤，通过折叠得到图④‎ ‎，再沿虚线剪去一个角，展开铺平后得到图⑤，其中FM，GN是折痕．若正方形EFGH与五边形MCNGF的面积相等，则FMGF的值是（　　）‎ A．‎5‎‎-‎‎2‎‎2‎ B．‎2‎‎-‎1 C．‎1‎‎2‎ D．‎‎2‎‎2‎ 二、填空题（本题有6小题，每小题4分，共24分）‎ ‎11．（4分）不等式3x﹣6≤9的解是　 　．‎ ‎12．（4分）数据3，4，10，7，6的中位数是　 　．‎ ‎13．（4分）当x＝1，y‎=-‎‎1‎‎3‎时，代数式x2+2xy+y2的值是　 　．‎ ‎14．（4分）如图，在量角器的圆心O处下挂一铅锤，制作了一个简易测倾仪．量角器的0刻度线AB对准楼顶时，铅垂线对应的读数是50°，则此时观察楼顶的仰角度数是　 　．‎ ‎15．（4分）元朝朱世杰的《算学启蒙》一书记载：“今有良马日行二百四十里，驽马日行一百五十里．驽马先行一十二日，问良马几何日追及之．”如图是两匹马行走路程s关于行走时间t的函数图象，则两图象交点P的坐标是　 　．‎ ‎16．（4分）图2，图3是某公共汽车双开门的俯视示意图，ME、EF、FN是门轴的滑动轨道，∠E＝∠F＝90°，两门AB、CD的门轴A、B、C、D都在滑动轨道上，两门关闭时（图2），A、D分别在E、F处，门缝忽略不计（即B、C重合）；两门同时开启，A、D分别沿E→M，F→N的方向匀速滑动，带动B、C滑动：B到达E时，C恰好到达F，此时两门完全开启，已知AB＝50cm，CD＝40cm．‎ ‎（1）如图3，当∠ABE＝30°时，BC＝　 　cm．‎ ‎（2）在（1）的基础上，当A向M方向继续滑动15cm时，四边形ABCD的面积为　 　cm2．‎ 三、解答题（本题有8小题，共66分，各小题都必须写出解答过程。）‎ ‎17．（6分）计算：|﹣3|﹣2tan60°‎+‎12‎+‎（‎1‎‎3‎）﹣1．‎ ‎18．（6分）解方程组‎3x-4(x-2y)=5，‎x-2y=1.‎ ‎19．（6分）某校根据课程设置要求，开设了数学类拓展性课程，为了解学生最喜欢的课程内容，随机抽取了部分学生进行问卷调查（每人必须且只选其中一项），并将统计结果绘制成如下统计图（不完整）．请根据图中信息回答问题：‎ ‎（1）求m，n的值．‎ ‎（2）补全条形统计图．‎ ‎（3）该校共有1200名学生，试估计全校最喜欢“数学史话”的学生人数．‎ ‎20．（8分）如图，在7×6的方格中，△ABC的顶点均在格点上．试按要求画出线段EF（E，F均为格点），各画出一条即可．‎ ‎21．（8分）如图，在▱OABC中，以O为圆心，OA为半径的圆与BC相切于点B，与OC相交于点D．‎ ‎（1）求BD的度数．‎ ‎（2）如图，点E在⊙O上，连结CE与⊙O交于点F，若EF＝AB，求∠OCE的度数．‎ ‎22．（10分）如图，在平面直角坐标系中，正六边形ABCDEF的对称中心P在反比例函数y‎=‎kx（k＞0，x＞0）的图象上，边CD在x轴上，点B在y轴上，已知CD＝2．‎ ‎（1）点A是否在该反比例函数的图象上？请说明理由；‎ ‎（2）若该反比例函数图象与DE交于点Q，求点Q的横坐标；‎ ‎（3）平移正六边形ABCDEF，使其一边的两个端点恰好都落在该反比例函数的图象上，试描述平移过程．‎ ‎23．（10分）如图，在平面直角坐标系中，正方形OABC的边长为4，边OA，OC分别在x轴，y轴的正半轴上，把正方形OABC的内部及边上，横、纵坐标均为整数的点称为好点．点P为抛物线y＝﹣（x﹣m）2+m+2的顶点．‎ ‎（1）当m＝0时，求该抛物线下方（包括边界）的好点个数．‎ ‎（2）当m＝3时，求该抛物线上的好点坐标．‎ ‎（3）若点P在正方形OABC内部，该抛物线下方（包括边界）恰好存在8个好点，求m的取值范围．‎ ‎24．（12分）如图，在等腰Rt△ABC中，∠ACB＝90°，AB＝14‎2‎，点D，E分别在边AB，BC上，将线段ED绕点E按逆时针方向旋转90°得到EF．‎ ‎（1）如图1，若AD＝BD，点E与点C重合，AF与DC相交于点O．求证：BD＝2DO．‎ ‎（2）已知点G为AF的中点．‎ ‎①如图2，若AD＝BD，CE＝2，求DG的长．‎ ‎②若AD＝6BD，是否存在点E，使得△DEG是直角三角形？若存在，求CE的长；若不存在，试说明理由．‎ ‎2019年浙江省丽水市中考数学试卷 参考答案与试题解析 一、选择题（本题有10小题，每小题3分，共30分）.‎ ‎1．（3分）实数4的相反数是（　　）‎ A．‎-‎‎1‎‎4‎ B．﹣4 C．‎1‎‎4‎ D．4‎ ‎【解答】解：∵符号相反，绝对值相等的两个数互为相反数，∴4的相反数是﹣4；‎ 故选：B．‎ ‎2．（3分）计算a6÷a3，正确的结果是（　　）‎ A．2 B．3a C．a2 D．a3‎ ‎【解答】解：由同底数幂除法法则：底数不变，指数相减知，a6÷a3＝a6﹣3＝a3．‎ 故选：D．‎ ‎3．（3分）若长度分别为a，3，5的三条线段能组成一个三角形，则a的值可以是（　　）‎ A．1 B．2 C．3 D．8‎ ‎【解答】解：由三角形三边关系定理得：5﹣3＜a＜5+3，‎ 即2＜a＜8，‎ 即符合的只有3，‎ 故选：C．‎ ‎4．（3分）某地一周前四天每天的最高气温与最低气温如表，则这四天中温差最大的是（　　）‎ 星期 一 二 三 四 最高气温 ‎10°C ‎12°C ‎11°C ‎9°C 最低气温 ‎3°C ‎0°C ‎﹣2°C ‎﹣3°C A．星期一 B．星期二 C．星期三 D．星期四 ‎【解答】解：星期一温差10﹣3＝7℃；‎ 星期二温差12﹣0＝12℃；‎ 星期三温差11﹣（﹣2）＝13℃；‎ 星期四温差9﹣（﹣3）＝12℃；‎ 故选：C．‎ ‎5．（3分）一个布袋里装有2个红球、3个黄球和5个白球，除颜色外其它都相同．搅匀后任意摸出一个球，是白球的概率为（　　）‎ A．‎1‎‎2‎ B．‎3‎‎10‎ C．‎1‎‎5‎ D．‎‎7‎‎10‎ ‎【解答】解：袋子里装有2个红球、3个黄球和5个白球共10个球，从中摸出一个球是白球的概率是‎5‎‎10‎‎=‎‎1‎‎2‎．‎ 故选：A．‎ ‎6．（3分）如图是雷达屏幕在一次探测中发现的多个目标，其中对目标A的位置表述正确的是（　　）‎ A．在南偏东75°方向处 B．在5km处 ‎ C．在南偏东15°方向5km处 D．在南偏东75°方向5km处 ‎【解答】解：由图可得，目标A在南偏东75°方向5km处，‎ 故选：D．‎ ‎7．（3分）用配方法解方程x2﹣6x﹣8＝0时，配方结果正确的是（　　）‎ A．（x﹣3）2＝17 B．（x﹣3）2＝14 C．（x﹣6）2＝44 D．（x﹣3）2＝1‎ ‎【解答】解：用配方法解方程x2﹣6x﹣8＝0时，配方结果为（x﹣3）2＝17，‎ 故选：A．‎ ‎8．（3分）如图，矩形ABCD的对角线交于点O．已知AB＝m，∠BAC＝∠α，则下列结论错误的是（　　）‎ A．∠BDC＝∠α B．BC＝m•tanα C．AO‎=‎m‎2sinα D．BD‎=‎mcosα ‎【解答】解：A、∵四边形ABCD是矩形，‎ ‎∴∠ABC＝∠DCB＝90°，AC＝BD，AO＝CO，BO＝DO，‎ ‎∴AO＝OB＝CO＝DO，‎ ‎∴∠DBC＝∠ACB，‎ ‎∴由三角形内角和定理得：∠BAC＝∠BDC＝∠α，故本选项不符合题意；‎ B、在Rt△ABC中，tanα‎=‎BCm，‎ 即BBC＝m•tanα，故本选项不符合题意；‎ C、在Rt△ABC中，AC‎=‎mcosα，即AO‎=‎m‎2cosα，故本选项符合题意；‎ D、∵四边形ABCD是矩形，‎ ‎∴DC＝AB＝m，‎ ‎∵∠BAC＝∠BDC＝α，‎ ‎∴在Rt△DCB中，BD‎=‎mcosα，故本选项不符合题意；‎ 故选：C．‎ ‎9．（3分）如图物体由两个圆锥组成．其主视图中，∠A＝90°，∠ABC＝105°，若上面圆锥的侧面积为1，则下面圆锥的侧面积为（　　）‎ A．2 B．‎3‎ C．‎3‎‎2‎ D．‎‎2‎ ‎【解答】解：∵∠A＝90°，AB＝AD，‎ ‎∴△ABD为等腰直角三角形，‎ ‎∴∠ABD＝45°，BD‎=‎‎2‎AB，‎ ‎∵∠ABC＝105°，‎ ‎∴∠CBD＝60°，‎ 而CB＝CD，‎ ‎∴△CBD为等边三角形，‎ ‎∴BC＝BD‎=‎‎2‎AB，‎ ‎∵上面圆锥与下面圆锥的底面相同，‎ ‎∴上面圆锥的侧面积与下面圆锥的侧面积的比等于AB：CB，‎ ‎∴下面圆锥的侧面积‎=‎2‎×‎1‎=‎‎2‎．‎ 故选：D．‎ ‎10．（3分）将一张正方形纸片按如图步骤，通过折叠得到图④，再沿虚线剪去一个角，展开铺平后得到图⑤，其中FM，GN是折痕．若正方形EFGH与五边形MCNGF的面积相等，则FMGF的值是（　　）‎ A．‎5‎‎-‎‎2‎‎2‎ B．‎2‎‎-‎1 C．‎1‎‎2‎ D．‎‎2‎‎2‎ ‎【解答】解：连接HF，设直线MH与AD边的交点为P，如图：‎ 由折叠可知点P、H、F、M四点共线，且PH＝MF，‎ 设正方形ABCD的边长为2a，‎ 则正方形ABCD的面积为4a2，‎ ‎∵若正方形EFGH与五边形MCNGF的面积相等 ‎∴由折叠可知正方形EFGH的面积‎=‎1‎‎5‎×‎正方形ABCD的面积‎=‎‎4‎‎5‎a‎2‎，‎ ‎∴正方形EFGH的边长GF‎=‎4‎‎5‎a‎2‎=‎2‎‎5‎‎5‎a ‎∴HF‎=‎‎2‎GF‎=‎2‎‎10‎‎5‎a ‎∴MF＝PH‎=‎2a-‎2‎‎10‎‎5‎a‎2‎=‎‎5-‎‎10‎‎5‎a ‎∴FMGF‎=‎‎5-‎‎10‎‎5‎a‎÷‎2‎‎5‎‎5‎a=‎‎5‎‎-‎‎2‎‎2‎ 故选：A．‎ 二、填空题（本题有6小题，每小题4分，共24分）‎ ‎11．（4分）不等式3x﹣6≤9的解是　x≤5　．‎ ‎【解答】解：3x﹣6≤9，‎ ‎3x≤9+6‎ ‎3x≤15‎ x≤5，‎ 故答案为：x≤5‎ ‎12．（4分）数据3，4，10，7，6的中位数是　6　．‎ ‎【解答】解：将数据重新排列为3、4、6、7、10，‎ ‎∴这组数据的中位数为6，‎ 故答案为：6．‎ ‎13．（4分）当x＝1，y‎=-‎‎1‎‎3‎时，代数式x2+2xy+y2的值是　‎4‎‎9‎　．‎ ‎【解答】解：当x＝1，y‎=-‎‎1‎‎3‎时，‎ x2+2xy+y2‎ ‎＝（x+y）2‎ ‎＝（1‎-‎‎1‎‎3‎）2‎ ‎=‎‎(‎2‎‎3‎)‎‎2‎‎ ‎ ‎=‎‎4‎‎9‎‎ ‎ 故答案为：‎4‎‎9‎．‎ ‎14．（4分）如图，在量角器的圆心O处下挂一铅锤，制作了一个简易测倾仪．量角器的0刻度线AB对准楼顶时，铅垂线对应的读数是50°，则此时观察楼顶的仰角度数是　40°　．‎ ‎【解答】解：过A点作AC⊥OC于C，‎ ‎∵∠AOC＝50°，‎ ‎∴∠OAC＝40°．‎ 故此时观察楼顶的仰角度数是40°．‎ 故答案为：40°．‎ ‎15．（4分）元朝朱世杰的《算学启蒙》一书记载：“今有良马日行二百四十里，驽马日行一百五十里．驽马先行一十二日，问良马几何日追及之．”如图是两匹马行走路程s关于行走时间t的函数图象，则两图象交点P的坐标是　（32，4800）　．‎ ‎【解答】解：令150t＝240（t﹣12），‎ 解得，t＝32，‎ 则150t＝150×32＝4800，‎ ‎∴点P的坐标为（32，4800），‎ 故答案为：（32，4800）．‎ ‎16．（4分）图2，图3是某公共汽车双开门的俯视示意图，ME、EF、FN是门轴的滑动轨道，∠E＝∠F＝90°，两门AB、CD的门轴A、B、C、D都在滑动轨道上，两门关闭时（图2），A、D分别在E、F处，门缝忽略不计（即B、C重合）；两门同时开启，A、D分别沿E→M，F→N的方向匀速滑动，带动B、C滑动：B到达E时，C恰好到达F，此时两门完全开启，已知AB＝50cm，CD＝40cm．‎ ‎（1）如图3，当∠ABE＝30°时，BC＝　90﹣45‎3‎　cm．‎ ‎（2）在（1）的基础上，当A向M方向继续滑动15cm时，四边形ABCD的面积为　2256　cm2．‎ ‎【解答】解：∵A、D分别在E、F处，门缝忽略不计（即B、C重合）且AB＝50cm，CD＝40cm．‎ ‎∴EF＝50+40＝90cm ‎∵B到达E时，C恰好到达F，此时两门完全开启，‎ ‎∴B、C两点的路程之比为5：4‎ ‎（1）当∠ABE＝30°时，在Rt△ABE中，BE‎=‎‎3‎‎2‎AB＝25‎3‎cm，‎ ‎∴B运动的路程为（50﹣25‎3‎）cm ‎∵B、C两点的路程之比为5：4‎ ‎∴此时点C运动的路程为（50﹣25‎3‎）‎×‎4‎‎5‎=‎（40﹣20‎3‎）cm ‎∴BC＝（50﹣25‎3‎）+（40﹣20‎3‎）＝（90﹣45‎3‎）cm 故答案为：90﹣45‎3‎；‎ ‎（2）当A向M方向继续滑动15cm时，设此时点A运动到了点A'处，点B、C、D分别运动到了点B'、C'、D'处，连接A'D'，如图：‎ 则此时AA'＝15cm ‎∴A'E＝15+25＝40cm 由勾股定理得：EB'＝30cm，‎ ‎∴B运动的路程为50﹣30＝20cm ‎∴C运动的路程为16cm ‎∴C'F＝40﹣16＝24cm 由勾股定理得：D'F＝32cm，‎ ‎∴四边形A'B'C'D'的面积＝梯形A'EFD'的面积﹣△A'EB'的面积﹣△D'FC'的面积‎=‎1‎‎2‎×90×(40+32)-‎1‎‎2‎×‎30×40‎-‎1‎‎2‎×‎24×32＝2256cm2．‎ ‎∴四边形ABCD的面积为2256cm2．‎ 故答案为：2256．‎ 三、解答题（本题有8小题，共66分，各小题都必须写出解答过程。）‎ ‎17．（6分）计算：|﹣3|﹣2tan60°‎+‎12‎+‎（‎1‎‎3‎）﹣1．‎ ‎【解答】解：原式‎=3-2‎3‎+2‎3‎+3=6‎．‎ ‎18．（6分）解方程组‎3x-4(x-2y)=5，‎x-2y=1.‎ ‎【解答】解：‎3x-4(x-2y)=5，①‎x-2y=1②.‎，‎ 将①化简得：﹣x+8y＝5 ③，‎ ‎②+③，得y＝1，‎ 将y＝1代入②，得x＝3，‎ ‎∴x=3‎y=1‎；‎ ‎19．（6分）某校根据课程设置要求，开设了数学类拓展性课程，为了解学生最喜欢的课程内容，随机抽取了部分学生进行问卷调查（每人必须且只选其中一项），并将统计结果绘制成如下统计图（不完整）．请根据图中信息回答问题：‎ ‎（1）求m，n的值．‎ ‎（2）补全条形统计图．‎ ‎（3）该校共有1200名学生，试估计全校最喜欢“数学史话”的学生人数．‎ ‎【解答】解：（1）观察条形统计图与扇形统计图知：选A的有12人，占20%，‎ 故总人数有12÷20%＝60人，‎ ‎∴m＝15÷60×100%＝25%‎ n＝9÷60×100%＝15%；‎ ‎（2）选D的有60﹣12﹣15﹣9﹣6＝18人，‎ 故条形统计图补充为：‎ ‎（3）全校最喜欢“数学史话”的学生人数为：1200×25%＝300人．‎ ‎20．（8分）如图，在7×6的方格中，△ABC的顶点均在格点上．试按要求画出线段EF（E，F均为格点），各画出一条即可．‎ ‎【解答】解：如图：‎ 从图中可得到AC边的中点在格点上设为E，过E作AB的平行线即可在格点上找到F，则EG平分BC；‎ EC‎=‎‎5‎，EF‎=‎‎5‎，FC‎=‎‎10‎，借助勾股定理确定F点，则EF⊥AC；‎ 借助圆规作AB的垂直平分线即可；‎ ‎21．（8分）如图，在▱OABC中，以O为圆心，OA为半径的圆与BC相切于点B，与OC相交于点D．‎ ‎（1）求BD的度数．‎ ‎（2）如图，点E在⊙O上，连结CE与⊙O交于点F，若EF＝AB，求∠OCE的度数．‎ ‎【解答】解：（1）连接OB，‎ ‎∵BC是圆的切线，∴OB⊥BC，‎ ‎∵四边形OABC是平行四边形，‎ ‎∴OA∥BC，∴OB⊥OA，‎ ‎∴△AOB是等腰直角三角形，‎ ‎∴∠ABO＝45°，‎ ‎∴BD的度数为45°；‎ ‎（2）连接OE，过点O作OH⊥EC于点H，设EH＝t，‎ ‎∵OH⊥EC，‎ ‎∴EF＝2HE＝2t，‎ ‎∵四边形OABC是平行四边形，‎ ‎∴AB＝CO＝EF＝2t，‎ ‎∵△AOB是等腰直角三角形，‎ ‎∴OA‎=‎‎2‎t，‎ 则HO‎=OE‎2‎-EH‎2‎=‎2t‎2‎-‎t‎2‎=‎t，‎ ‎∵OC＝2OH，‎ ‎∴∠OCE＝30°．‎ ‎22．（10分）如图，在平面直角坐标系中，正六边形ABCDEF的对称中心P在反比例函数y‎=‎kx（k＞0，x＞0）的图象上，边CD在x轴上，点B在y轴上，已知CD＝2．‎ ‎（1）点A是否在该反比例函数的图象上？请说明理由；‎ ‎（2）若该反比例函数图象与DE交于点Q，求点Q的横坐标；‎ ‎（3）平移正六边形ABCDEF，使其一边的两个端点恰好都落在该反比例函数的图象上，试描述平移过程．‎ ‎【解答】解：（1）过点P作x轴垂线PG，连接BP，‎ ‎∵P是正六边形ABCDEF的对称中心，CD＝2，‎ ‎∴BP＝2，G是CD的中点，‎ ‎∴PG‎=‎‎3‎，‎ ‎∴P（2，‎3‎），‎ ‎∵P在反比例函数y‎=‎kx上，‎ ‎∴k＝2‎3‎，‎ ‎∴y‎=‎‎2‎‎3‎x，‎ 由正六边形的性质，A（1，2‎3‎），‎ ‎∴点A在反比例函数图象上；‎ ‎（2）D（3，0），E（4，‎3‎），‎ 设DE的解析式为y＝mx+b，‎ ‎∴‎3m+b=0‎‎4m+b=‎‎3‎，‎ ‎∴m=‎‎3‎b=-3‎‎3‎，‎ ‎∴y‎=‎‎3‎x﹣3‎3‎，‎ 联立方程y=‎‎2‎‎3‎xy=‎3‎x-3‎‎3‎解得x‎=‎‎3+‎‎17‎‎2‎，‎ ‎∴Q点横坐标为‎3+‎‎17‎‎2‎；‎ ‎（3）E（4，‎3‎），F（3，2‎3‎），‎ 将正六边形向左平移两个单位后，E（2，‎3‎），F（1，2‎3‎），‎ 则点E与F都在反比例函数图象上；‎ ‎23．（10分）如图，在平面直角坐标系中，正方形OABC的边长为4，边OA，OC分别在x轴，y轴的正半轴上，把正方形OABC的内部及边上，横、纵坐标均为整数的点称为好点．点P为抛物线y＝﹣（x﹣m）2+m+2的顶点．‎ ‎（1）当m＝0时，求该抛物线下方（包括边界）的好点个数．‎ ‎（2）当m＝3时，求该抛物线上的好点坐标．‎ ‎（3）若点P在正方形OABC内部，该抛物线下方（包括边界）恰好存在8个好点，求m的取值范围．‎ ‎【解答】解：（1）如图1中，当m＝0时，二次函数的表达式y＝﹣x2+2，函数图象如图1所示．‎ ‎∵当x＝0时，y＝2，当x＝1时，y＝1，‎ ‎∴抛物线经过点（0，2）和（1，1），‎ 观察图象可知：好点有：（0，0），（0，1），（0，2），（1，0），（1，1），共5个．‎ ‎（2）如图2中，当m＝3时，二次函数解析式为y＝﹣（x﹣3）2+5．如图2．‎ ‎∵当x＝1时，y＝1，当x＝2时，y＝4，当x＝4时，y＝4，‎ ‎∴抛物线经过（1，1），（2，4），（4，4），‎ 共线图象可知，抛物线上存在好点，坐标分别为（1，1），（2，4），（4，4）．‎ ‎（3）如图3中，∵抛物线的顶点P（m，m+2），‎ ‎∴抛物线的顶点P在直线y＝x+2上，‎ ‎∵点P在正方形内部，则0＜m＜2，‎ 如图3中，E（2，1），F（2，2），观察图象可知，当点P在正方形OABC 内部，该抛物线下方（包括边界）恰好存在8个好点时，抛物线与线段EF有交点（点F除外），‎ 当抛物线经过点E时，﹣（2﹣m）2+m+2＝1，‎ 解得m‎=‎‎5-‎‎13‎‎2‎或‎5+‎‎13‎‎2‎（舍弃），‎ 当抛物线经过点F时，﹣（2﹣m）2+m+2＝2，‎ 解得m＝1或4（舍弃），‎ ‎∴当‎5-‎‎13‎‎2‎‎≤‎m＜1时，顶点P在正方形OABC内部，该抛物线下方（包括边界）恰好存在8个好点．‎ ‎24．（12分）如图，在等腰Rt△ABC中，∠ACB＝90°，AB＝14‎2‎，点D，E分别在边AB，BC上，将线段ED绕点E按逆时针方向旋转90°得到EF．‎ ‎（1）如图1，若AD＝BD，点E与点C重合，AF与DC相交于点O．求证：BD＝2DO．‎ ‎（2）已知点G为AF的中点．‎ ‎①如图2，若AD＝BD，CE＝2，求DG的长．‎ ‎②若AD＝6BD，是否存在点E，使得△DEG是直角三角形？若存在，求CE的长；若不存在，试说明理由．‎ ‎【解答】（1）证明：如图1中，‎ ‎∵CA＝CB，∠ACB＝90°，BD＝AD，‎ ‎∴CD⊥AB，CD＝AD＝BD，‎ ‎∵CD＝CF，‎ ‎∴AD＝CF，‎ ‎∵∠ADC＝∠DCF＝90°，‎ ‎∴AD∥CF，‎ ‎∴四边形ADFC是平行四边形，‎ ‎∴OD＝OC，‎ ‎∵BD＝2OD．‎ ‎（2）①解：如图2中，作DT⊥BC于点T，FH⊥BC于H．‎ 由题意：BD＝AD＝CD＝7‎2‎，BC‎=‎‎2‎BD＝14，‎ ‎∵DT⊥BC，‎ ‎∴BT＝TC＝7，‎ ‎∵EC＝2，‎ ‎∴TE＝5，‎ ‎∵∠DTE＝∠EHF＝∠DEF＝90°，‎ ‎∴∠DET+∠TDE＝90°，∠DET+∠FEH＝90°，‎ ‎∴∠TDE＝∠FEH，‎ ‎∵ED＝EF，‎ ‎∴△DTE≌△EHF（AAS），‎ ‎∴FH＝ET＝5，‎ ‎∵∠DDBE＝∠DFE＝45°，‎ ‎∴B，D，E，F四点共圆，‎ ‎∴∠DBF+∠DEF＝90°，‎ ‎∴∠DBF＝90°，‎ ‎∵∠DBE＝45°，‎ ‎∴∠FBH＝45°，‎ ‎∵∠BHF＝90°，‎ ‎∴∠HBF＝∠HFB＝45°，‎ ‎∴BH＝FH＝5，‎ ‎∴BF＝5‎2‎，‎ ‎∵∠ADC＝∠ABF＝90°，‎ ‎∴DG∥BF，‎ ‎∵AD＝DB，‎ ‎∴AG＝GF，‎ ‎∴DG‎=‎‎1‎‎2‎BF‎=‎‎5‎‎2‎‎2‎．‎ ‎②解：如图3﹣1中，当∠DEG＝90°时，F，E，G，A共线，作DT⊥BC于点T，FH⊥BC于H．设EC＝x．‎ ‎∵AD＝6BD，‎ ‎∴BD‎=‎‎1‎‎7‎AB＝2‎2‎，‎ ‎∵DT⊥BC，∠DBT＝45°，‎ ‎∴DT＝BT＝2，‎ ‎∵△DTE≌△EHF，‎ ‎∴EH＝DT＝2，‎ ‎∴BH＝FH＝12﹣x，‎ ‎∵FH∥AC，‎ ‎∴EHEC‎=‎FHAC，‎ ‎∴‎2‎x‎=‎‎12-x‎'14‎，‎ 整理得：x2﹣12x+28＝0，‎ 解得x＝6±2‎2‎．‎ 如图3﹣2中，当∠EDG＝90°时，取AB的中点O，连接OG．作EH⊥AB于H．‎ 设EC＝x，由2①可知BF‎=‎‎2‎（12﹣x），OG‎=‎‎1‎‎2‎BF‎=‎‎2‎‎2‎（12﹣x），‎ ‎∵∠EHD＝∠EDG＝∠DOG＝90°，‎ ‎∴∠ODG+∠OGD＝90°，∠ODG+∠EDH＝90°，‎ ‎∴∠DGO＝∠HDE，‎ ‎∴△EHD∽△DOG，‎ ‎∴DHOG‎=‎EHDO，‎ ‎∴‎2‎2‎-‎2‎‎2‎(14-x)‎‎2‎‎2‎‎(12-x)‎‎=‎‎2‎‎2‎‎(14-x)‎‎5‎‎2‎，‎ 整理得：x2﹣36x+268＝0，‎ 解得x＝18﹣2‎14‎或18+2‎14‎（舍弃），‎ 如图3﹣3中，当∠DGE＝90°时，取AB的中点O，连接OG，CG，作DT⊥BC于T，FH⊥BC于H，EK⊥CG于K．设EC＝x．‎ ‎∵∠DBE＝∠DFE＝45°，‎ ‎∴D，B，F，E四点共圆，‎ ‎∴∠DBF+∠DEF＝90°，‎ ‎∵∠DEF＝90°，‎ ‎∴∠DBF＝90°，‎ ‎∵AO＝OB，AG＝GF，‎ ‎∴OG∥BF，‎ ‎∴∠AOG＝∠ABF＝90°，‎ ‎∴OG⊥AB，‎ ‎∵OG垂直平分线段AB，∵CA＝CB，‎ ‎∴O，G，C共线，‎ 由△DTE≌△EHF，可得EH＝DT＝BT＝2，ET＝FH＝12﹣x，BF‎=‎‎2‎（12﹣x），OG‎=‎‎1‎‎2‎BF‎=‎‎2‎‎2‎（12﹣x），CK＝EK‎=‎‎2‎‎2‎x，GK＝7‎2‎‎-‎‎2‎‎2‎（12﹣x）‎-‎‎2‎‎2‎x，‎ 由△OGD∽△KEG，可得OGEK‎=‎ODGK，‎ ‎∴‎2‎‎2‎‎(12-x)‎‎2‎‎2‎x‎=‎‎5‎‎2‎‎7‎2‎-‎2‎‎2‎(12-x)-‎2‎‎2‎x，‎ 解得x＝2，‎ ‎，综上所述，满足条件的EC的值为6±2‎2‎或18﹣2‎14‎或2．‎ 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/6/30 9:36:13；用户：中考培优辅导；邮箱：p5193@xyh.com；学号：27411521‎