【40套试卷合集】江苏省南京市二十九中致远校区2019-2020学年数学九上期末模拟试卷含答案 10页

2019-2020 学年九上数学期末模拟试卷含答案 （满分 150 分 ，考试时间 120 分钟） 一、选择题（本大题共 10 小题，每小题 4 分，共 40 分．每小题只有一个正确的选项） 1．若式子 x 3 在实数范围内有意义，则 x 的取值范围是（ ） A． x ＞ 3 B ．x≥ 3 C ．x＜ 3 D ．x≤ 3 2．下面的图形中，中心对称图形的是（ ） A． B ． C ． D ． 3．如图， AB 是⊙ O 的弦， OC⊥ AB于点 C，若 AB=8cm，OC=3cm，则⊙ O 的半径为 ( ) A．3 cm B ．5 cm C ．6 cm D ．10 cm 4．下列事件是不可能事件的是（ ） A．掷一次质地均 匀的正方体骰子，向上的一面是 6 点 B．在只装有红 球和绿球的袋子中摸出一个球，结果是黄球 C．经过城市中 某一有交通信号灯的路口，遇到绿灯 D．通常加热到 100℃时，水沸腾 A C B O （第 3 题） 5．下列二次根式中，属于最简二次根式的是 （ ） A 1 x ； B 8 ； C 2 x2 ； D x 2 1 6．商品原价 289 元，经连续两次降价后售价为 256 元，设平均每次降价的百分率为 x，则下面所列方程 正确的是 ( ) A、 289(1 x)2 256 B 、 256(1 x)2 289 C 、 289(1 2x) 256 D 、 256(1 2x ) 289 7．已知⊙ O1 和⊙ O2 的半径分别是 2 cm 和 3cm， 若 O1 O 2 =1cm，则⊙ O1 和⊙ O2 的位置关系是 （ ） A. 外切 B. 内含 C. 内切 D. 相交 8. 一个不透明的布袋中装着只有颜色不同的红、黄、白色三种小球，其中红色小球有 8 个，黄、白色 小 球的数目相同 . 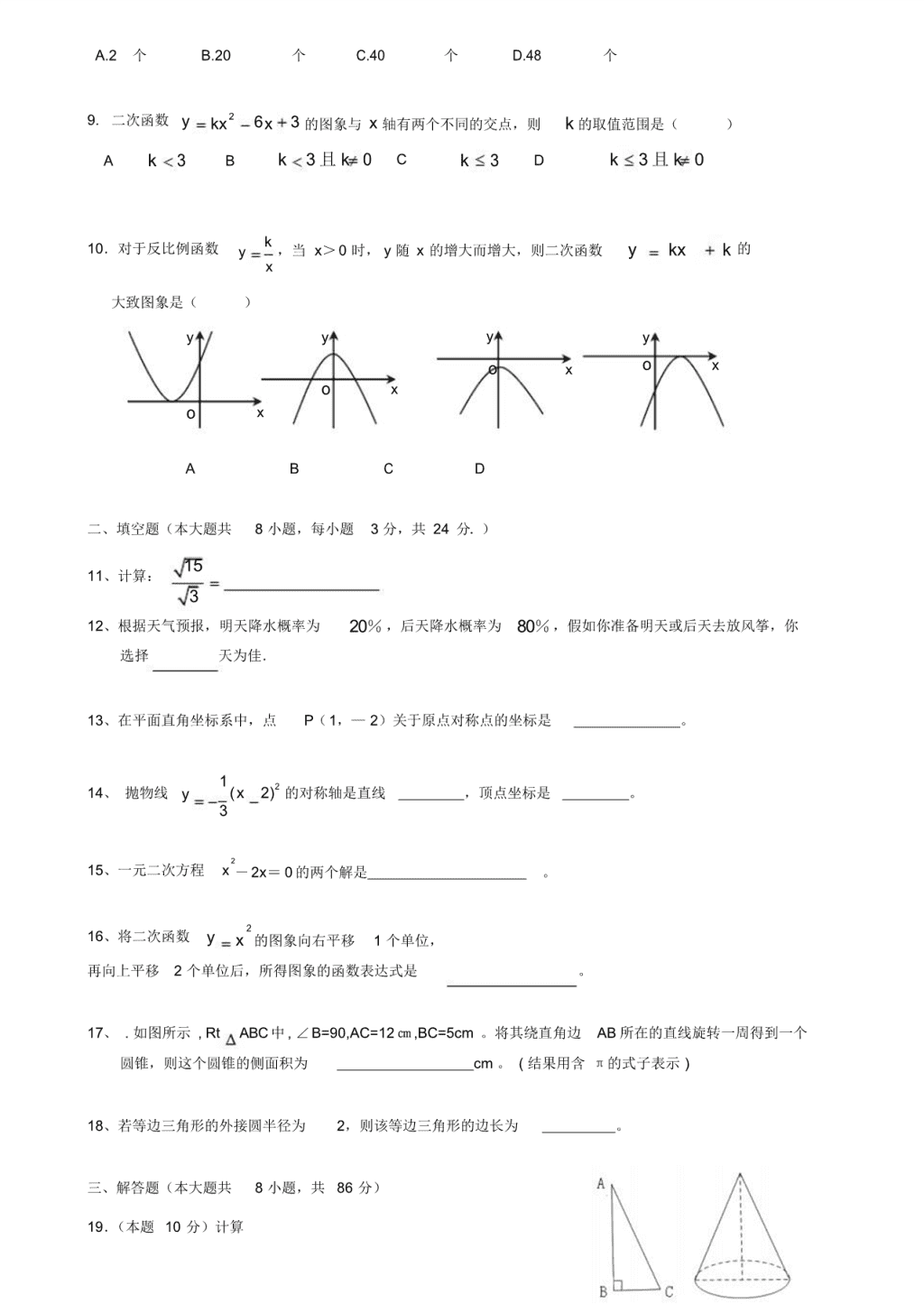为估计袋中黄色 小球的数目，每次将袋中小球搅匀后摸出一个小球记下颜色，然后放回 袋中，再次搅匀 多次试验发现摸到红球的频率是 1 ，则估计黄色小球的数目是（ ） 6 2 A.2 个 B.20 个 C.40 个 D.48 个 9. 二次函数 y kx 2 6x 3 的图象与 x 轴有两个不同的交点，则 k 的取值范围是（ ） A k 3 B k 3 且 k 0 C k 3 D k 3 且 k 0 10．对于反比例函数 y k ，当 x＞ 0 时， y 随 x 的增大而增大，则二次函数 y x kx k 的 大致图象是（ ） y y y y o x o x o x o x A B C D 二、填空题（本大题共 8 小题，每小题 3 分，共 24 分．） 11、计算： 15 3 12、根据天气预报，明天降水概率为 20％ ，后天降水概率为 80％，假如你准备明天或后天去放风筝，你 选择 天为佳． 13、在平面直角坐标系中，点 P（1，— 2）关于原点对称点的坐标是 。 14、 抛物线 y 1(x 2)2 的对称轴是直线 ，顶点坐标是 。 3 15、一元二次方程 x 2 －2x＝ 0 的两个解是 。 16、将二次函数 y 2 x 的图象向右平移 1 个单位， 再向上平移 2 个单位后，所得图象的函数表达式是 。 17、 . 如图所示 , Rt ABC 中 , ∠B=90,AC=12 ㎝,BC=5cm 。将其绕直角边 AB 所在的直线旋转一周得到一个 圆锥，则这个圆锥的侧面积为 cm 。 ( 结果用含 π的式子表示 ) 18、若等边三角形的外接圆半径为 2，则该等边三角形的边长为 。 三、解答题（本大题共 8 小题，共 86 分） 19．（本题 10 分）计算 （1） 3 8 50 18 （2） (3 5)(2 5) 20、（本题 10 分）用适当的方法解方程 （ 1） 2 x －2x－1＝ 0 （2） 3x(x 2) 5( x 2) 21、（本题 10 分）如图，四边形 ABCD 是平行四边形，以 AB 为直径的⊙ O 经过点 D，E 是⊙ O 上一点，且 ∠ AED＝ 45o． 试判断 CD 与⊙ O 的关系，并说明理由． D C A O B E （第 21 题） 22、( 本题 10 分) 如图，在边长为 1 的小正方形组成的格中，△ AOB 的顶点均在格点上，点 A、B 的坐标分别 为A（-2 ，3）、B（-3 ，1） . △ AOB绕点 O 顺时针旋转 90°后得到△ A1OB1。 （1）画出△ A1OB1； （2）点 A1的坐标为 ； （3）点 A 旋转到点 A1 所经过的路线长为 。（结果保留 π ） A B O 2 23．（本题 10 分）某商场开展购物抽奖活动，抽奖箱中有 4 个标号分别为 1、2、 3、 4 的质地、大小相同 的小球，顾客任意摸取一个小球，然后放回，再摸取一个小球，若两次摸出的数字之和为“ 8”是一等奖， 数字之和为“ 6”是二等奖，数字之和为其它数字则是三等。 （1）请用列表法 ( 或画树状图 ) 表示顾客所有可能摸到的情况。 （2）请分别求出顾客抽中一、二、三等奖的概率 . 24．（本题 10 分）如图，⊙ O的直径 AB为 10cm，弦 AC为 6cm，∠ ACB的平分线交⊙ O于D，求四边形 ADBC的面 积。 C A B O D 第 24 题 25．（本题 12 分）一直角三角形的两直角边的和为 20cm，设其中一直角边长为 xcm， （ 1）试写出该直角三角形面积 s 关于 x 的函数关系式； 并求出当这个直角三角形面积最大时直角三角 形的两直角边长分别为多少？最大面积是多少？ （ 2）试计算当这个直角三角形面积为 32 cm 时，两直角边长分别为多少？ 26、（本题 14 分）已知：抛物线 y x 2 bx c 与 x 轴的两个交点分别为 A（1， 0）和 B（3， 0），与 y 轴交于点 C。 （ 1）确定此二次函数的解析式及顶点 D的坐标； （ 2）将直线 CD 沿 y轴向下平移 3 个单位长度，求平移后直线 m 的解析式； （ 3）在直线 m 上是否存在一点 E，使得以点 E、A、B、C为顶点的四边形是梯形，如果存在，请直接写 出所有满足条件的 E 点的坐标。（不必写出过程） y C O A B x D 第 26 题 2019-2020 学年九上数学期末模拟试卷含答案 一、选择题 1.如图，两个圆柱体紧靠在一起，它的主视图是（ ）. 从正面看 A B C D 2 2．方程 x 4 0 的根是（ ）. A. x =2 B. x =-2 C.x1 2, x2 2 D. x =4 3.用配方法解一元二次方程 2 x 4x 5 ，配方正确的是（ ） A. (x 2 2) 1 B. (x 2 2) 1 C. (x 2 2) 9 D.(x 2 2) 9 4.如图， AC=AD，BC=BD，则下列结论正确的有（ ） A. AD 垂直平分 CD B. CD 垂直平分 AB C. AB 与 CD互相垂直平分 D. CD 平分∠ ACB 5.如图所示，若点 A 在平行四边形区域上作随机运动，则点 A 落在阴影区域内的概率是（ ） 1 1 A. B. 6 5 1 1 C. D. 4 3 6.如图，在菱形 ABCD 中，对角线 AC，BD 相较于点 O，E为 BC的中点， 则下列式子中， 不．成．立．的是（ ） A.OE=BE=CE B.BC=2OE C. AC=2OE D. AB=2OE C D C A B O E D 第 4 题图 第 5 题图 A B 第 6题图 2 7.一元二次方程 x 5x 2 0 的两个根分别为 x1,x2 ,则x1 x2 x1 x2 的值是 （ ） A. -7 B. 7 C. 3 D. -3 8.电影院座位号呈阶梯状或下坡状的原因是（ ） A.减小盲区 B. 增大盲区 C. 盲区不变 D. 为了美观 9.反比例函数 y k 3 的图像，当 x＞0 时， y 随 x 的值增大而增大，则 k 的取值范围是（ ） x A. k＜ 3 B. k≤ 3 C. k＞3 D. k≥3 10.如图，在等腰梯形 ABCD 中，AD∥BC，过 D 作 DF⊥BC,垂足为 F，若 AD=3，BC=9，AB=5，则 DF 的长为 （ ） A. 5 B. 5 C. 3 D. 4 11.菱形 OABC 在平面直角坐标系中的位置如图所示，∠ AOC=45°，OC= 2 ，点 B 的坐标为（ ） A. ( 2 1, 1) B. (1, 2 1) C. ( 2, 1) D.(1, 2) y A A D C B O A x B F 第 10 题图 C C 第 11 题 图 B 第 12 题图 12.如图所示， A,B,C 分别表示三个村庄， AB=1000 米， BC=600 米， AC=800 米，拟建一个文化活动中心， 若活动中心 P 到这个村庄的距离相等，则， P的位置应在（ ） . A. AB 的中点 B. BC 的中点 C. AC 的中点 D. ∠C 的平分线与 AB 的交点 13.若关于 x 的一元二次方程 x2 2x k 0 有两个不相等的实数根，则 k 的取值范围是（ ）. A. k＜ 1 B. k ＜-1 C. k＞1 D. k＞-1 14.小稠和小海两人都要从甲、乙、丙三个社区中随机选取一个社区参加综合实践活动，那么他们选到同 一个社区参加实践活动的概率为（ ）. 1 1 1 1 A. B. C. D. 2 3 6 9 k 15.关于 x 的函数 y=k(x+1)和 y (k 0) 在同一坐标系中的图像大致是（ ） x A B C D 二、解答题 16．解方程： 2 (x 3) ( x 3) 0 ． 17.如图，已知∠ C=∠D=90°，AC 与 BD 交于 O， AC=BD. D C （ 1）求证： BC=AD （2）求证：点 O 在线段 AB 的垂直平分线上 . O A B 第 17 题图 ． )，求 与 V 之间的函数关系式； 18.如图， AB和 DE是直立在地面上的两根立柱， AB=5m，某一时刻 AB在阳光下的投影 BC=2.5m. （1）请你再图中画 出此时 DE 在阳光下的投影 EF； （2）测量 AB 的投影时，同时测量出 DE在阳光下的投影 EF长为 5m，请你计算 DE 的长. D A B C E 第 18 题图 19.一个袋子中装有 3 个红球和两个黄球，它们除颜色外，其他都相同 . （1）求从袋中摸出一个球是红球的概率； （ 2）将 n 个绿球（与红、黄球除颜色外，其他都相同）放入袋中摇均匀，从袋中随机摸出一个球，记下 颜色，再 把它放回袋中，不断重复上述的过程，共摸了 500 次，其中 60 次摸到红球 .请通过计算估计 n 的 值. 20.某物质在质量不变的情况下， 她的密度 (kg/m 3 )与体积 V(m 3 )成反比例函数关系， 根据以下条件， 解答 下列问题： （ 1）已知 V=3(m3)， =2(kg/m 3 （2）若该物质的体积由 a (m3)增加到 a +2(m 3)，而密度却由 6(kg/m 3)减少到 b (kg/m 3)，求 a 和 b 的值 . 21.如图， BD 为矩形 ABCD 的对角线，∠ ADB，∠ DBC 的平分线分别交于 AB,CD 于 E,F 点. （1）求证：四边形 DEBF 为平行四边形； （ 2）连接 EF，若 EF⊥ BD，且 AD=6，求菱形 DEBF 的面积 . D F C A E B 第 21 题图 22.某校初中义务交于服务范围内学生人数持续增加， 2012 年学生数比 2011 年增加了 a %，2013 年学生数 比 2012 年多了 100 人，这样 2013 年学生人数就比 2011 年增加了 2a%. （1）求 2012 年学生人数比 2011 年多多少人？ （2）由于教学楼改造， 2013 年的教室总面积比 2011 年增加了 2.5 a %，因而 2013 年每个学生人平均教室 面积比 2011 年增加了 1 24 ，达到了 1 2 a(m ) .求该校 2013 年的教室总面积 . 8 23.如图 ① ，A（ 4，0），C（0，n）分别是 x 和 y 轴上的点， n＞0,以 OA,OC 为边在第一象限内作矩形 OABC， 对角线 OB， AC，交于点 D 双曲线 y k （x＞0,k＞0）交边 BC 于 G，交边 AB 于 H； x （1）设直线 AC的函数关系式为 y qx p ，请用含 n 的代数式表示 q 和 p. （2）求证： BG BH ; BC BA （3）如图 ② ，若上述双曲线经过点 D，判断点 D 是否是双曲线与直线 AC 唯一的交点，请说明理由 . y y k x C G B D H y y k x O A 第 23 题图 ① x x 第 23 题图② 24.正方形 ABCD 中，将一个直角三角板的直角顶点与点 A 重合，一条直角边与边 BC 交于点 E（点 E 不与 点 B 和点 C重合），另一条直角边与边 CD 的延长线交于点F. （1）如图 ① ，求证： AE=AF； （2）如图 ② ，此直角三角板有一个角是 45°，它的斜边 MN 与边 CD 交于点 G，且点 G 是斜边 MN 的中点， 连接 EG，求证： EG=BE+DG. （3）在（ 2）的条件下，如果 AB GF 5 ，那么点 G 是否一定是边 CD 的中点？请说明理由 . 6 第 24 题图① 第 24 题图② 九年级数学 一．选择题（ 3 分×15=45 分）