人教版九年级数学上册期中检测卷【含答案】 44页

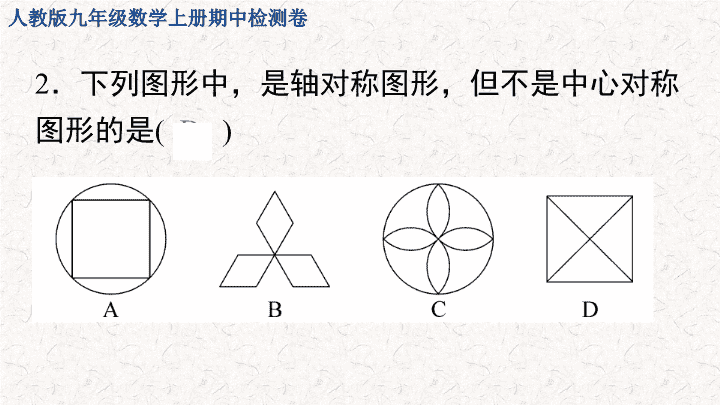
期中检测卷 时间： 120 分钟 总分： 120 分 一、选择题 ( 每小题 3 分，共 30 分 ) 1 ．抛物线 y ＝ x 2 － 2 x ＋2的顶点坐标为 ( A ) A ． (1 ， 1 ) B．(－1， 1) C ． (1 ， 3 ) D．(－1， 3) 2 ．下列图形中，是轴对称图形，但不是中心对称图形的是 ( B ) 3．一元二次方程 x 2 ＋ 2 x ＋1＝0的解是 ( C ) A ． x 1 ＝ 1 ， x 2 ＝－ 1 B ． x 1 ＝ x 2 ＝ 1 C ． x 1 ＝ x 2 ＝－ 1 D ． x 1 ＝－ 1 ， x 2 ＝ 2 4 ．已知 x ＝－1是关于 x 的方程 x 2 ＋ mx ＋ n ＝0的一个根，则代数式 m 2 ＋ n 2 － 2 mn 的值为 ( C ) A ．0 B．－ 1 C ．1 D．±1 5 ．二次函数 y ＝ a 2 x 2 ＋ bx ＋ c ( a ≠0)的图象的顶点为 P ( m ， k )且有一点 Q ( k ， m )也在该函数图象上，则下列结论一定正确的是 ( C ) A ． m ＝ k B ． m ＞ k C ． m ≥ k D． m ＜ k 6 ．如图，二次函数 y ＝ ax 2 ＋ bx ＋ c 的图象经过点 A (1 ， 0) ， B (5 ， 0) ，下列说法正确的是 ( D ) A ． c ＜ 0 B． b 2 － 4 ac ＜ 0 C ． a － b ＋ c ＜ 0 D．图象的对称轴是直线 x ＝ 3 7 ．如图，把 △ ABC 绕顶点 C 按顺时针方向旋转得到 △ A ′ B ′ C ，当 A ′ B ′⊥ AC 于点 D ， ∠ A ＝ 47° ， ∠ A ′ CB ＝ 128° 时， ∠ B ′ CA 的度数为 ( C ) A ．44° B．43° C ．42° D．40° 8 ．已知 x ≠ y ，且 x 2 － x ＝ 10 ， y 2 － y ＝ 10 ，则 x ＋ y ＝ ( A ) A ．1 B．－ 1 C ．5 D．－ 5 9 ．如图，在平面直角坐标系中，将边长为1的正方形 OABC 绕点 O 顺时针旋转 45° 后得到正方形 OA 1 B 1 C 1 ，依此方式，绕点 O 连续旋转2019次得到正方形 OA 2019 B 2019 C 2019 ，那么点 A 2019 的坐标是 ( A ) A ． B ． (1 ， 0) C ． D ． (0 ，－ 1) 10 ．关于 x 的一元二次方程 ax 2 ＋ bx ＋ ＝0有一个根是－1，若二次函数 y ＝ ax 2 ＋ bx ＋ 的图象的顶点在第一象限，设 t ＝ 2 a ＋ b ，则 t 的取值范围是 ( D ) A. ＜ t ＜ B ．－1＜ t ≤ C ．－ ≤ t ＜ D ．－1＜ t ＜ 解析：∵关于 x 的一元二次方程 ax 2 ＋ bx ＋ ＝0有一个根是－1， ∴ 二次函数 y ＝ ax 2 ＋ bx ＋ 的图象过点(－1， 0 )．∴ a － b ＋ ＝0.又∵ t ＝ 2 a ＋ b ， ∴ a ＝ ， b ＝ .∵ 二次函数 y ＝ ax 2 ＋ bx ＋ 的图象的顶点在第一象限，且过点(－1， 0) ， ， ∴ － >0 ，图象开口向下，即 a <0. ∴ b >0.∴ <0 ， >0.解得－1＜ t ＜ . 故选 D. 二、填空题 ( 每小题 3 分，共 24 分 ) 11 ．若二次函数 y ＝ ax 2 ＋ bx 的图象开口向下，则 a______ 0( 填“＝”或“＞”或“＜”)． 12 ．已知 x 1 ， x 2 是方程 x 2 － x －3＝0的两根，则 ＝ ________. < 13 ．如图， △ ABC 为等边三角形， △ AO ′ B 绕点 A 逆时针旋转后能与 △ AOC 重合．若 AO ＝ 3 ，则点 O ′ ， O 之间的距离为 _________. 3 14 ．有一块长为 32 cm 、宽为 24 cm 的长方形纸片，在每个角上截去相同的正方形，再折起来做成一个无盖的盒子，已知盒子的底面积是原纸片面积的一半，则盒子的高是 _______cm. 15 ．已知关于 x 的一元二次方程 ax 2 ＋ 2 x ＋2－ c ＝0有两个相等的实数根，则 ＋ c 的值等于 ______. 4 2 16 ．廊桥是我国古老的文化遗产，如图是某座抛物线形廊桥的示意图．已知抛物线的函数表达式 物线上距水面 AB 高为8米的点 E ， F 处要安装两盏警示灯，则这两盏灯的水平距离 EF 是 ____ 米． 为 y ＝－ x 2 ＋ 10 ，为保护廊桥的安全，在该抛 17 ．如图， △ ABC 、 △ BDE 都是等腰直角三角形， BA ＝ BC ， BD ＝ BE ， AC ＝ 4 ， DE ＝ 2 .将△ BDE 绕点 B 逆时针方向旋转后得 △ BD ′ E ′ ，当点 E ′恰好落在线段 AD ′上时，则 CE ′ ＝ ________. 向旋转后得 △ BD ′ E ′ ， ∴ D ′ B ＝ BE ′＝ BD ＝ 2 ， ∠ D ′ BE ′ ＝ 90° ＝ ∠ ABC .∴∠ ABD ′ ＝ ∠ CBE ′. 解析：如图，连接 CE ′.∵△ ABC 、 △ BDE 都是等腰直角三角形， BA ＝ BC ， BD ＝ BE ， AC ＝ 4 ， DE ＝ ∴ AB ＝ BC ＝ ， BD ＝ BE ＝2.∵将△ BDE 绕点 B 逆时针方 ∴△ ABD ′ ≌ △ CBE ′(SAS )．∴∠ D ′＝∠ CE ′ B ＝ 45°. 过 B 作 BH ⊥ CE ′于 H .在 Rt△ BHE ′ 中， BH ＝ E ′ H ＝ ，在 Rt△ BCH 中， CH ＝ ＝ ， ∴ CE ′ ＝ . 18 ．某一房间内 A ， B 两点之间设有探测报警装置，小车(不计大小)在房间内运动，当小车从 AB 之间经过时，将触发报警．现将 A ， B 两点放置于平面直角坐标系 xOy 中(如图)，已知点 A ， B 的坐标分别为 (0 ， 4) ， (5 ， 4) ，小车沿抛物线 y ＝ ax 2 － 2 ax － 3 a 运动．若小车在运动过程中只触发一次报警，则 a 的取值范围是 ____________________________. 或 或 解析：抛物线 y ＝ ax 2 － 2 ax － 3 a ＝ a ( x － 1) 2 － 4 a ＝ a ( x ＋ 1)( x － 3) ， ∴ 其对称轴为直线 x ＝ 1 ，且图象与 x 轴交于(－1， 0) ， (3 ， 0 )．①∵抛物线顶点为(1，－ 4 a ) ，当顶点在线段 AB 上时，－ 4 a ＝ 4 ， ∴ a ＝－1；②当抛物线过点(0， 4 )时，代入解析 式得4＝－3 a ， ∴ a ＝－ . 由对称轴为直线 x ＝1及图象与 x 轴交于(－ 1 ， 0) ， (3 ， 0 )可知，当 a ＜－ 时，抛物线与线段 AB 只有一个交点； ③ 当抛物线过点 (5 ， 4 )时，代入解析式得 25 a － 10 a － 3 a ＝ 4 ， ∴ a ＝ .同理可知，当 a ＞ 时，抛物线与线段 AB 只有一个交点．综上， a ＝－1或 a ＜－ 或 a ＞ . 三、解答题 ( 共 66 分 ) 19 ．(8分)解方程： (1) x 2 － 2 x －8＝0； 解： x 1 ＝－ 2 ， x 2 ＝4.(4分) (2)( x － 2)( x －5)＝－2. 解： x 1 ＝ 3 ， x 2 ＝4.(8分) 20 ．(8分)如图，在由边长为1的小正方形组成的方格纸上，将 △ ABC 绕着点 A 顺时针旋转 90°. (1)画出旋转之后的△ AB ′ C ′； 解： △ AB ′ C ′如图所示．(4分) (2)求线段 AC 在旋转过程中扫过的扇形的面积． 解：由图可知 AC ＝ 2 ， 所以线段 AC 在旋转过程中扫过的扇形的面积 S 即为半径为2的圆的面积的 ， 故 S ＝ π·2 2 ＝ π. (8分 ) 21 ．(8分)已知二次函数 y ＝ a ( x － h ) 2 ，当 x ＝2时， y 有最大值，且函数图象过点(－1，－3)． (1)求二次函数的解析式； 解：根据题意，得 y ＝ a ( x － 2) 2 ， 把(－1，－3)代入，得－3＝ a (－1－2) 2 ， ∴ 二次函数的解析式为 y ＝－ ( x － 2) 2 . (4分) 解得 a ＝－ ， (2)当 x 为何值时， y 随 x 的增大而增大？ 解：∵抛物线的对称轴为直线 x ＝ 2 ， 抛物线开口向下， ∴ 当 x ＜2时， y 随 x 的增大而增大．(8分) 22 ．(10分)关于 x 的方程 x 2 － (2 k － 1) x ＋ k 2 － 2 k ＋3＝0有两个不相等的实数根． (1)求实数 k 的取值范围； 解：∵方程有两个不相等的实数根， ∴ Δ ＝[－(2 k － 1)] 2 － 4( k 2 － 2 k ＋3)＝4 k －11＞0. 解得 k ＞ .(4分) (2)设方程的两个实数根分别为 x 1 、 x 2 ，是否存在实数 k ，使得 | x 1 | － | x 2 | ＝ ？若存在，求出 k 的值；若不存在，说明理由． 解：存在． ∵ x 1 ＋ x 2 ＝ 2 k － 1 ， x 1 x 2 ＝ k 2 － 2 k ＋3＝( k － 1) 2 ＋ 2 ＞ 0 ， ∴ x 1 ， x 2 同号． ∵ k ＞ ， ∴2 k －1＞ . ∴ x 1 ＞ 0 ， x 2 ＞0.(7分) ∴ 将 | x 1 | － | x 2 | ＝ 两边平方可得 即 ( x 1 ＋ x 2 ) 2 － 4 x 1 x 2 ＝ 5 ， 代入得 (2 k － 1) 2 － 4( k 2 － 2 k ＋3)＝5， 即 4 k －11＝5， 解得 k ＝4.(10分) 23 ．(10分)网络销售是一种重要的销售方式．某乡镇农贸公司新开设了一家网店，销售当地农产品．其中一种当地特产在网上试销售，其成本为每千克10元．公司在试销售期间，调查发现，每天的销售量 y (kg )与销售单价 x (元)满足如图所示的函数关系(其中10＜ x ≤30)． (1)直接写出 y 与 x 之间的函数关系式及自变量的取值范围； 解：易得 y 与 x 之间的函数关系式为 (3分) 解：∵(14－10)×640＝2560， 2560 ＜ 3100 ， ∴ x ＞ 14. ∴( x －10)(－20 x ＋920)＝3100. 解得 x 1 ＝41(不合题意舍去)， x 2 ＝ 15. 答：每天的利润要达到3100元，销售单价 x 应定为15元．(7分) ( 2)若农贸公司每天销售该特产的利润要达到3100元，则销售单价 x 应定为多少元？ (3)设每天销售该特产的利润为 W 元，若14＜ x ≤30 ，则销售单价 x 为多少元时，每天的销售利润最大？最大利润是多少元？ 解：当14＜ x ≤30时， W ＝ ( x －10)(－20 x ＋920)＝－20( x － 28) 2 ＋ 6480. ∵ －20＜0， 14 ＜ x ≤30 ， ∴ 当 x ＝28时，每天的销售利润最大，最大利润是6480元．(10分) 24 ．(10分)如图①是实验室中的一种摆动装置， BC 在地面上，支架 ABC 是底边为 BC 的等腰直角三角形，摆动臂 AD 可绕点 A 旋转，摆动臂 DM 可绕点 D 旋转， AD ＝ 30 ， DM ＝ 10. (1)在旋转过程中． (1)① AM ＝ AD ＋ DM ＝ 40 ，或 AM ＝ AD － DM ＝20.(2分) ① 当 A ， D ， M 三点在同一直线上时，求 AM 的长； ②当 A ， D ， M 三点为同一直角三角形的顶点时，求 AM 的长； 解： 显然 ∠ MAD 不能为直角．当 ∠ AMD 为直角时， AM 2 ＝ AD 2 － DM 2 ＝ 30 2 － 10 2 ＝ 800 ， ∴ AM ＝ 20 (－20 舍去)． 当 ∠ ADM ＝ 90° 时， AM 2 ＝ AD 2 ＋ DM 2 ＝ 30 2 ＋ 10 2 ＝ 1000 ， ∴ AM ＝ 10 (－10 舍去)． 综上所述，满足条件的 AM 的长为 20 或 10 . (5分) (2)若摆动臂 AD 顺时针旋转 90°, 点 D 的位置由 △ ABC 外的点 D 1 转到其内的点 D 2 处，连接 D 1 D 2 ，如图 ② ，此时 ∠ AD 2 C ＝ 135° ， CD 2 ＝ 60 ，求 BD 2 的长． 解：如图②，连接 CD 1 . 由题意得 ∠ D 1 AD 2 ＝ 90° ， AD 1 ＝ AD 2 ＝ 30 ， ∴∠ D 1 AD 2 ＝ 45° ， D 1 D 2 ＝ 30. ∵∠ AD 2 C ＝ 135° ， ∴∠ CD 2 D 1 ＝ 90°. ∴ CD 1 ＝ ∵∠ BAC ＝ ∠ D 1 AD 2 ＝ 90° ， ∴∠ BAC － ∠ CAD 2 ＝ ∠ D 1 AD 2 － ∠ CAD 2 . ∴∠ BAD 2 ＝ ∠ CAD 1 . ∵ AB ＝ AC ， AD 2 ＝ AD 1 ， ∴△ BAD 2 ≌ △ CAD 1 (SAS )． ∴ BD 2 ＝ CD 1 ＝ 30 .(10分) 25 ．(12分)如图，点 A ， B ， C 都在抛物线 y ＝ ax 2 － 2 amx ＋ am 2 ＋ 2 m －5(其中－ 4(1) ＜ a ＜0)上， AB ∥ x 轴， ∠ ABC ＝ 135° ，且 AB ＝ 4. (1)填空：抛物线的顶点坐标为 ___________ (用含 m 的代数式表示)； (3分) ( m ， 2 m －5) 解析： ∵ y ＝ ax 2 － 2 amx ＋ am 2 ＋ 2 m － 5 ＝ a ( x － m ) 2 ＋ 2 m － 5 ， ∴ 抛物线的顶点坐标为 ( m ， 2 m －5)． (2)求△ ABC 的面积(用含 a 的代数式表示)； 解：过点 C 作直线 AB 的垂线，交线段 AB 的延长线于点 D ，如图所示． ∵ AB ∥ x 轴，且 AB ＝ 4 ， ∴ 点 B 的坐标为 ( m ＋ 2 ， 4 a ＋ 2 m －5)． ∵∠ ABC ＝ 135° ， ∴ 设 BD ＝ t ，则 CD ＝ t . ∴ 点 C 的坐标为 ( m ＋2＋ t ， 4 a ＋ 2 m －5－ t )． ∵ 点 C 在抛物线 y ＝ a ( x － m ) 2 ＋ 2 m －5上， ∴4 a ＋ 2 m －5－ t ＝ a (2＋ t ) 2 ＋ 2 m － 5. 整理，得 at 2 ＋ (4 a ＋ 1) t ＝ 0 ， ∴ S △ ABC ＝ AB · CD ＝－ .(7分) 解得 t 1 ＝0(舍去)， t 2 ＝－ . ( 3)若△ ABC 的面积为 2 ，当 2 m － 5≤ x ≤2 m －2时， y 的最大值为 2 ，求 m 的值． ∴ 抛物线的解析式为 y ＝－ ( x － m ) 2 ＋ 2 m － 5. 解： ∵△ ABC 的面积为 2 ， ∴ ＝2. 解得 a ＝－ . 分三种情况考虑： ①当 m ＞ 2 m － 2 ，即 m ＜2时， 解得 m 1 ＝7－ (舍去)， m 2 ＝ 7 ＋ (舍去)； 整理，得 m 2 － 14 m ＋39＝0， 有－ (2 m －2－ m ) 2 ＋ 2 m － 5 ＝2. ② 当 2 m － 5≤ m ≤2 m － 2 ，即 2≤ m ≤5 时， 解得 m ＝ ； 有 2 m －5＝2， 综上所述： m 的值为 或10＋ 2 .(12分) ③ 当 m ＜ 2 m － 5 ，即 m ＞ 5 时， 有－ (2 m －5－ m ) 2 ＋ 2 m －5＝2， 整理，得 m 2 － 20 m ＋60＝0， 解得 m 3 ＝10－ 2 (舍去)， m 4 ＝ 10 ＋ 2 .