沪科版八年级数学上册期中测试题（含答案） 10页

沪科版八年级数学上册期中测试题（含答案）‎ ‎(考试时间：120分钟　　　满分：150分)‎ 分数：__________‎ 一、选择题(本大题共10小题，每小题4分，满分40分)‎ 每小题都给出A、B、C、D四个选项，其中只有一个是正确的．‎ ‎1．点P(－2，5)所在的象限是(　B　)‎ A．一 B．二 C．三 D．四 ‎2．在函数y＝中，自变量x的取值范围是(　A　)‎ A．x≠2 B．x≥2 C．x＜2 D．x≤2‎ ‎3．下列命题是真命题的是(　C　)‎ A．直角三角形中两个锐角互补 B．相等的角是对顶角 C．同旁内角互补，两直线平行 D．若|a|＝|b|，则a＝b ‎4．已知P(0，－4)，Q(6，1)，将线段PQ平移至P1Q1，若P1(m，－3)，Q1(3，n)，则mn的值是(　D　)‎ A．－8 B．8 C．－9 D．9‎ ‎5．若一个三角形的三条边长分别为3，2a－1，6，则整数a的值可能是(　B　)‎ A．2，3 B．3，4‎ C．2，3，4 D．3，4，5‎ ‎6．已知点A(－2，y1)，B(－3，y2)，C(3，y3)都在关于x的一次函数y＝－x＋m的图象上，则y1，y2，y3之间的大小关系是(　D　)‎ A．y1＞y2＞y3 B．y1＜y2＜y3‎ C．y2＜y1＜y3 D．y3＜y1＜y2‎ ‎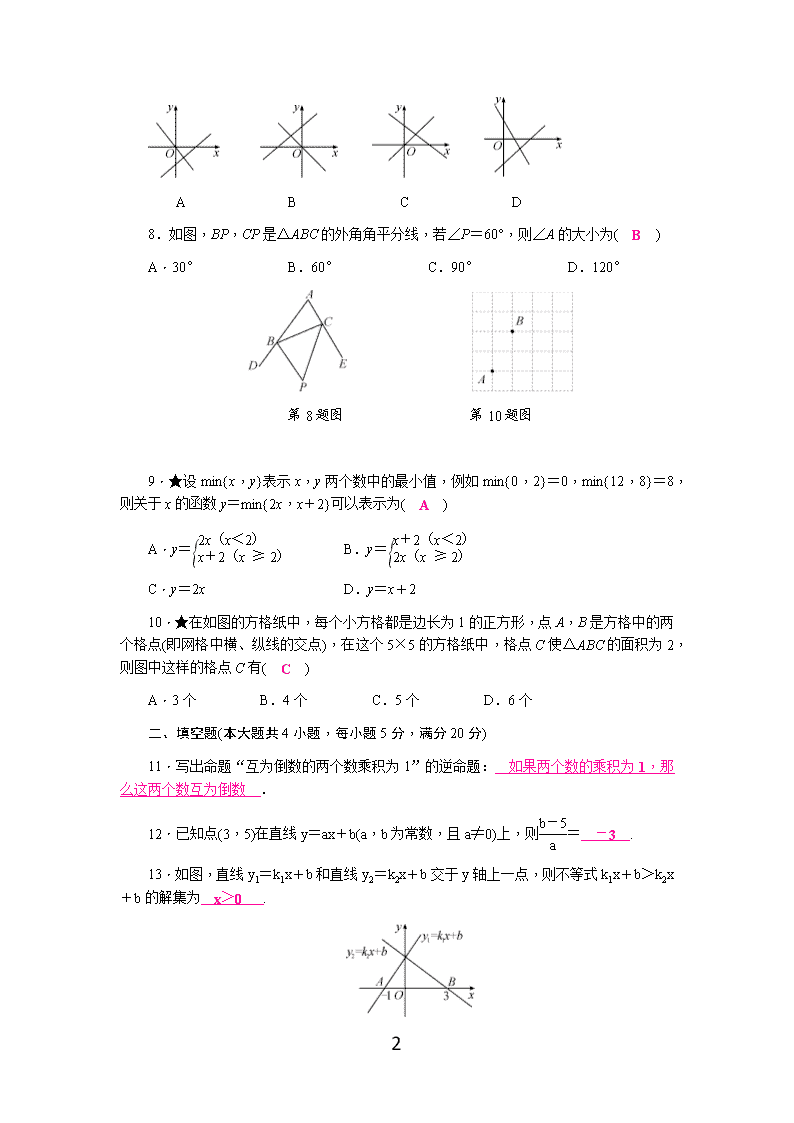7．在同一平面直角坐标系中，函数y＝kx与y＝－k的图象大致是(　B　)‎ 10‎ ‎ ‎ A B C D ‎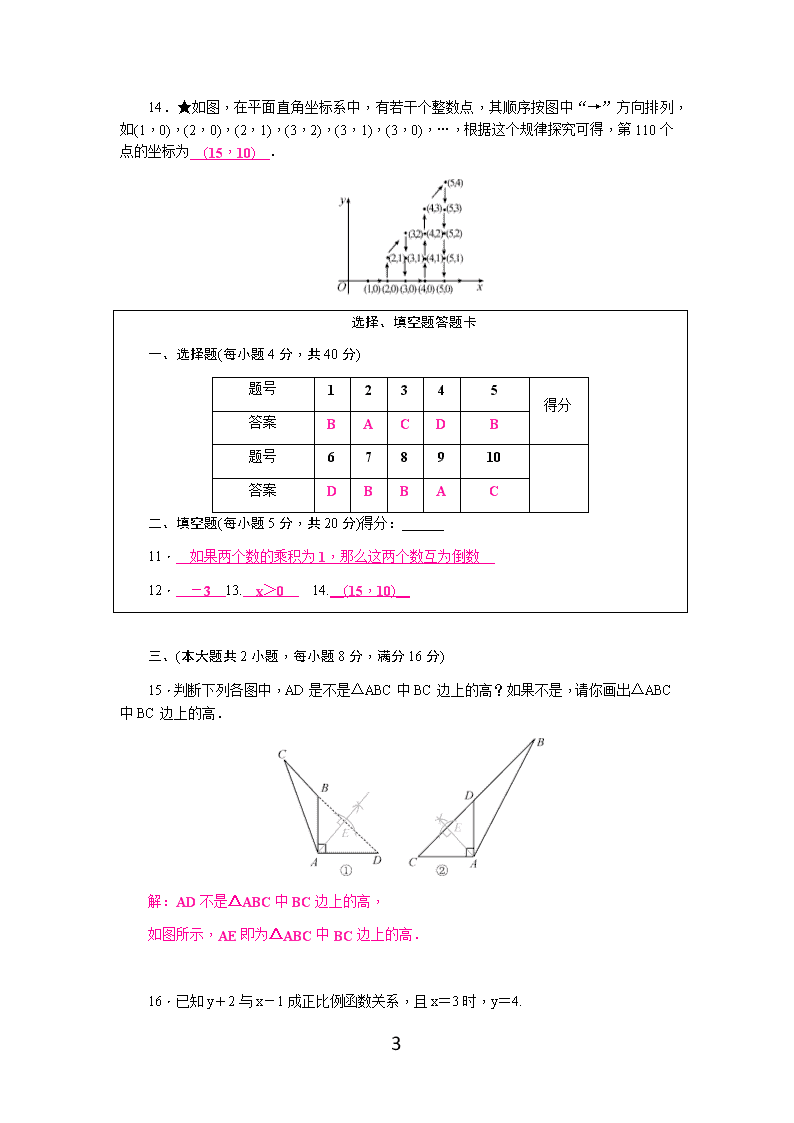8．如图，BP，CP是△ABC的外角角平分线，若∠P＝60°，则∠A的大小为(　B　)‎ A．30° B．60° C．90° D．120°‎ ‎ ‎ 第8题图　　 　第10题图 ‎9．★设min{x，y}表示x，y两个数中的最小值，例如min{0，2}＝0，min{12，8}＝8，则关于x的函数y＝min{2x，x＋2}可以表示为(　A　)‎ A．y＝ B．y＝ C．y＝2x D．y＝x＋2‎ ‎10．★在如图的方格纸中，每个小方格都是边长为1的正方形，点A，B是方格中的两个格点(即网格中横、纵线的交点)，在这个5×5的方格纸中，格点C使△ABC的面积为2，则图中这样的格点C有(　C　)‎ A．3个 B．4个 C．5个 D．6个 二、填空题(本大题共4小题，每小题5分，满分20分)‎ ‎11．写出命题“互为倒数的两个数乘积为1”的逆命题：__如果两个数的乘积为1，那么这两个数互为倒数 ．‎ ‎12．已知点(3，5)在直线y＝ax＋b(a，b为常数，且a≠0)上，则＝ －3 .‎ ‎13．如图，直线y1＝k1x＋b和直线y2＝k2x＋b交于y轴上一点，则不等式k1x＋b＞k2x＋b的解集为 x＞0 .‎ 10‎ ‎14．★如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如(1，0)，(2，0)，(2，1)，(3，2)，(3，1)，(3，0)，…，根据这个规律探究可得，第110个点的坐标为__(15，10)__．‎ 选择、填空题答题卡 一、选择题(每小题4分，共40分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 得分 答案 B A C D B 题号 ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 D B B A C 二、填空题(每小题5分，共20分)得分：______‎ ‎11．__如果两个数的乘积为1，那么这两个数互为倒数__‎ ‎12． －3　13. x＞0 　14.__(15，10)__‎ 三、(本大题共2小题，每小题8分，满分16分)‎ ‎15．判断下列各图中，AD是不是△ABC中BC边上的高？如果不是，请你画出△ABC中BC边上的高．‎ 解：AD不是△ABC中BC边上的高，‎ 如图所示，AE即为△ABC中BC边上的高．‎ ‎16．已知y＋2与x－1成正比例函数关系，且x＝3时，y＝4.‎ 10‎ ‎(1)求y与x之间的函数表达式；‎ ‎(2)求当x＝－2时，y的值．‎ 解：(1)设y＋2＝k(x－1)(k≠0)，‎ 当x＝3，y＝4时，4＋2＝k(3－1)，解得k＝3，‎ ‎∴y＋2＝3(x－1)，‎ 即y＝3x－5.‎ ‎(2)当x＝－2时，y＝3×(－2)－5＝－11.‎ 四、(本大题共2小题，每小题8分，满分16分)‎ ‎17．已知点A(m＋2，3)和点B(m－1，2m－4)，且AB∥x轴．‎ ‎(1)求m的值；‎ ‎(2)求AB的长．‎ 解：(1)∵A(m＋2，3)和点B(m－1，2m－4)，且AB∥x轴，‎ ‎∴2m－4＝3，‎ ‎∴m＝.‎ ‎(2)由(1)得m＝，‎ ‎∴m＋2＝，m－1＝，2m－4＝3，‎ ‎∴A，B.‎ ‎∵－＝3，‎ ‎∴AB的长为3.‎ ‎18．如图，在△ABC中，∠BAC＝90°，∠B＝50°，AE，CF是角平分线，它们相交于点O，AD是高，求∠BAD和∠AOC的度数．‎ 10‎ 解：∵AD是高，‎ ‎∠B＝50°，‎ ‎∴Rt△ABD中，∠BAD＝90°－50°‎ ‎＝40°.‎ ‎∵∠BAC＝90°，∠B＝50°，‎ ‎∴△ABC中，∠ACB＝90°－50°＝40°.‎ ‎∵AE，CF是角平分线，‎ ‎∴∠CAE＝∠CAB＝45°，‎ ‎∠ACF＝∠ACB＝20°，‎ ‎∴△AOC中，∠AOC＝180°－45°－20°＝115°.‎ 五、(本大题共2小题，每小题10分，满分20分)‎ ‎19．已知△ABC在平面直角坐标系中的位置如图所示．将△ABC向右平移6个单位，再向下平移6个单位得到△A1B1C1.(图中每个小方格边长均为1个单位)‎ ‎(1)在图中画出平移后的△A1B1C1；‎ ‎(2)直接写出△A1B1C1各顶点的坐标：A1____；B1________；C1________；‎ ‎(3)求出△ABC的面积．‎ 解：(1)如图，△A1B1C1即为所求．‎ 10‎ ‎(2)由图可知，A1(4，－2)；B1(1，－4)；C1(2，－1)．‎ 故答案为：(4，－2)；(1，－4)；(2，－1)．‎ ‎(3)S△ABC＝3×3－×1×3－×1×2－×2×3＝.‎ ‎20．已知：如图，AC，BD相交于点O，DF平分∠CDO交AC于点F，BE平分∠ABO交AC于点E，∠A＝∠C.记∠CDF＝∠1，∠OBE＝∠2.求证：∠1＝∠2.‎ 证明：∵∠A＝∠C，‎ ‎∴DC∥AB，‎ ‎∴∠CDO＝∠ABO.‎ ‎∵DF平分∠CDO，BE平分∠ABO，‎ ‎∴∠1＝∠CDO，‎ ‎∠2＝∠ABO，‎ ‎∴∠1＝∠2.‎ 六、(本题满分12分)‎ ‎21．(东至县期末)如图，直线y＝kx＋1(k≠0)与y轴，x轴分别交于点A，B.直线y＝－2x＋4与y轴交于点C，与直线y＝kx＋1交于点D.△ACD的面积为.‎ ‎(1)求k的值；‎ ‎(2)直接写出不等式x＋1＜－2x＋4的解集；‎ ‎(3)点P在x轴上，如果△DBP的面积为4，求点P的坐标．‎ 10‎ 解：(1)当x＝0时，y＝kx＋1＝1，则A(0，1)，‎ 当x＝0时，y＝－2x＋4＝4，则C(0，4)．‎ 设D点的坐标为(t，－2t＋4)，‎ ‎∵△ACD的面积为，‎ ‎∴×(4－1)×t＝，解得t＝1，‎ ‎∴D(1，2)，‎ 把D(1，2)代入y＝kx＋1得k＋1＝2，‎ ‎∴k＝1.‎ ‎(2)不等式x＋1＜－2x＋4的解集为x＜1.‎ ‎(3)当y＝0时，x＋1＝0，‎ 解得x＝－1，则B(－1，0)，‎ 设P(m，0)，‎ ‎∵△DBP的面积为4，‎ ‎∴×|m＋1|×2＝4，解得m＝3或－5，‎ ‎∴P点坐标为(－5，0)或(3，0)．‎ 10‎ 七、(本题满分12分)‎ ‎22．甲、乙两人在一条笔直的公路上同向匀速而行，甲从A点开始追赶乙，甲、乙两人之间的距离y(m)与追赶的时间x(s)的关系如图所示．已知乙的速度为5 m/s.‎ ‎(1)求甲、乙两人之间的距离y(m)与追赶的时间x(s)之间的函数关系式；‎ ‎(2)甲从A点追赶乙，经过40 s，求甲前行的距离；‎ ‎(3)若甲追赶10 s后，甲的速度增加1.2 m/s，请求出10秒后甲、乙两人之间的距离y(m)与追赶的时间x(s)之间的函数关系式，并在图中画出它的图象．‎ 解：(1)设y＝kx＋b(k≠0)，‎ ‎∵函数图象经过点(0，90)，(50，0)，‎ ‎∴解得 ‎∴y＝－x＋90.‎ ‎(2)5×40＋90－ ‎＝200＋90－(－72＋90)‎ ‎＝272.‎ 答：甲前行的距离为272 m.‎ ‎(3)∵甲的速度为272÷40＝6.8 m/s，‎ ‎∴甲的速度增加后为6.8＋1.2＝8 m/s，‎ x＝10时，y＝－×10＋90＝72 m，‎ 由题意得，相遇时，5(x－10)＋72＝8(x－10)，‎ 解得x＝34，‎ ‎①10＜x≤34时，y＝5(x－10)＋72－8(x－10)＝－3x＋102，‎ ‎②x＞34时，y＝8(x－34)－5(x－34)＝3x－102，‎ 10‎ 画出函数图象如图所示．‎ 八、(本题满分14分)‎ ‎23．(肥东县期末)为加强校园文化建设，某校准备打造校园文化墙，需用甲、乙两种石材．经市场调查，甲种石材的费用y(元)与使用面积x(m2)间的函数关系如图所示，乙种石材的价格为每平方米50元．‎ ‎(1)求y与x间的函数表达式；‎ ‎(2)若校园文化墙总面积共600 m2，其中使用甲石材x m2，设购买两种石材的总费用为w元，请直接写出w与x间的函数表达式；‎ ‎(3)在(2)的前提下，若甲种石材使用面积多于300 m2，且不超过乙种石材面积的2倍，那么应该怎样分配甲、乙两种石材的面积才能使总费用最少？最少总费用为多少元？‎ 解：(1)y＝ ‎(2)使用甲种石材x m2，则使用乙种石材(600－x)m2.‎ 当0≤x≤300时，‎ w＝80x＋50(600－x)＝30x＋30 000.‎ 当x＞300时，‎ w＝30x＋15 000＋50(600－x)＝－20x＋45 000.‎ ‎∴w＝ ‎(3)设甲种石材为x m2，则乙种石材(600－x) m2，‎ ‎∴ ‎∴300＜x≤400，‎ 由(2)知w＝－20x＋45 000，‎ 10‎ ‎∵k＝－20＜0，‎ ‎∴w随x的增大而减小，‎ 即甲种石材400 m2，乙种石材200 m2时，‎ wmin＝－20×400＋45 000＝37 000.‎ 答：甲种石材400 m2，乙种石材200 m2时，总费用最少，最少总费用为37 000元．‎ 10‎