2020九年级数学上册 第二十四章 圆 24 3页

1 24.3 正多边形和圆 ※教学目标※ 【知识与技能】 了解正多边形的有关概念，掌握用等分圆周画圆的内接正多边形的方法.能根据定义判 定一个多边形是否是正多边形，理解正多边形和圆的关系. 【过程与方法】 领会“特殊—一般—特殊”是认识事物的重要方法.使学生会等分圆周，利用等分圆周 的方法构造正多边形，并会设计图案，发展学生的实践能力和创新精神. 【情感态度】 通过观察、发现、探究等活动，感受数学来源于生活，服务于生活，体现事物之间是相 互联系，相互作用的. 【教学重点】 正多边形和圆的相关概念及其之间的运算. 【教学难点】 探索正多边形和圆的关系，正多边形半径，中心角、弦心距，边长之间的关系. ※教学过程※ 一、情境导入 请同学们观察课件中出示的图片，提问： （1）你能从图案中找出多边形吗？什么样的图形叫正多边形？ （2）正多边形与圆有怎样的关系？ 二、探索新知 问题 1 把一个圆分成 5 等份，求证：依次连接各分点所得的五边形是这个圆的内接正 五边形. 证明：如图，把⊙O 分成相等的 5 段弧，依次连接各分点所得到五 边形 ABCDE. ∵ ， ∴AB=BC=CD=DE=EA, . ∴∠A=∠B. 同理∠B=∠C=∠D=∠E， ∴五边形 ABCDE 是正五边形. 问题 2 如果将圆 n 等分，依次连接各分点得到一个 n 边形，这个 n 边形一定是正 n 边 形吗？ 答案：一定. 问题 3 各边相等的圆内接多边形是正多边形吗？各角相等的圆内接多边形是正多边形 吗？如果是，说明理由；如果不是，举出反例.     AB BC CD DE EA= = = =   3BCE CDA AB= = 2 答案：各边相等的圆内接多边形是正多边形.理由如下：因为各边相等的圆内接多边形 的各角也相等.各角相等的圆内接多边形不是正多边形，如矩形. 归纳总结 一个正多边形的外接圆的圆心叫做这个正多边形的中心， 外接圆的半径叫做正多边形的半径，正多边形每一边所对的圆心角叫做正 多边形的中心角，中心到正多边形的一边的距离叫做正多边形的边心距. 例 有一个亭子,它的地基是半径为 4m 的正六边形,求地基的周长和 面积（结果保留小数点后一位）. 解：如图，连接OB，OC.因为六边形 ABCDEF 是正六边形，所以它的中心角等于 =60 °，△OBC 是等边三角形，从而正六边形的边长等于它的半径.因此,亭子地基的周长 l=4×6=24（m）.作 OP⊥BC，垂足为 P.在 Rt△OPC 中,OC=4m，PC= =2m，利用勾股定 理,可得边心距 r= = （m）.亭子地基的面积 S= lr= ×24× ≈41.6（m2）. 想一想 你知道如何利用正多边形和圆的关系来画正多边形吗？ 画正多边形，通常是通过等分圆周的方法来画的.等分圆周有两种方式： （1）用量角器等分圆周 方法 1：由于在同圆或等圆中相等的圆周角所对弧相等，因此作相等的圆心角可以等分 圆. 方法 2：先用量角器画一个等于 的圆心角，这个圆心角所对的弧就是圆的 ，然 后在圆上依次截取这条弧的等弧，就得到圆的几等分点. 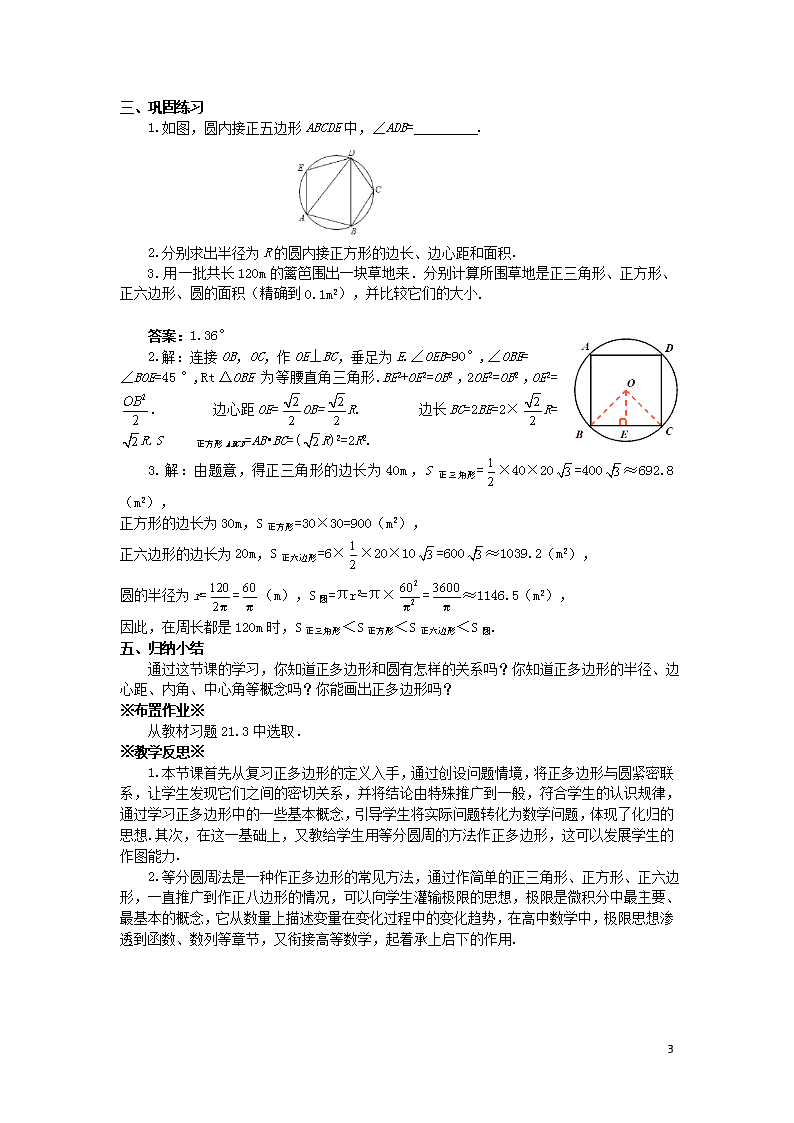（2）用尺规等分圆 正六边形的作法 方法 1：画一个圆，用量角器画一个等于 =60°的圆心角，它对着一段弧，然后在 圆上依次截取与这条弧相等的弧，就得到圆的 6 个等分点，依次连接各等分点，即可得到正 六边形.（如图①） 方法 2：在半径为 R 的圆上依次截取等于 R 的弦，就可以把圆六等分，顺次连接各分点 即可得到半径为 R 的正六边形.（如图②） 正四边形的作法 用直尺和圆规作两条互相垂直的直径，就可以把圆四等分，从而作出正方形.（如图 ③） ① ② ③ 360 6  4 2 2 BC = 2 24 2− 2 3 1 2 1 2 2 3 360 n  1 n 360 6  3 三、巩固练习 1.如图，圆内接正五边形 ABCDE 中，∠ADB= . 2.分别求出半径为 R 的圆内接正方形的边长、边心距和面积. 3.用 一批共长 120m 的篱笆围出一块草地来．分别计算所围草地是正三角形、正方形、 正六边形、圆的面积（精确到 0.1m2），并比较它们的大小. 　　答案：1.36° 2.解：连接 OB，OC，作 OE⊥BC，垂足为 E.∠OEB=90°,∠OBE= ∠BOE=45°,Rt△ OBE 为等腰直角三角形.BE2+OE2=OB2 ，2OE2=OB2 ，OE2= . 边心距 OE= OB= R. 边长 BC=2BE=2× R= R.S 正 方 形 ABCD=AB•BC=( R)2=2R2. 3.解：由题意，得正三角形的边长为 40m， S 正三角形= ×40×20 =400 ≈692.8 （m2）， 正方形的边长为 30m，S 正方形=30×30=900（m2）， 正六边形的边长为 20m，S 正六边形=6× ×20×10 =600 ≈1039.2（m2）， 圆的半径为 r= = （m），S 圆=πr2=π× = ≈1146.5（m2）， 因此，在周长都是 120m 时，S 正三角形＜S 正方形＜S 正六边形＜S 圆. 五、归纳小结 通过这节课的学习，你知道正多边形和圆有怎样的关系吗？你知道正多边形的半径、边 心距、内角、中心角等概念吗？你能画出正多边形吗？ ※布置作业※ 从教材习题 21.3 中选取． ※教学反思※ 1.本节课首先从复习正多边形的定义入手，通过创设问题情境，将正多边形与圆紧密联 系，让学生发现它们之间的密切关系，并将结论由特殊推广到一般，符合学生的认识规律， 通过学习正多边形中的一些基本概念，引导学生将实际问题转化为数学问题，体现了化归的 思想.其次，在这一基础上，又教给学生用等分圆周的方法作正多边形，这可以发展学生的 作图能力. 2.等分圆周法是一种作正多边形的常见方法，通过作简单的正三角形、正方形、正六边 形，一直推广到作正八边形的情况，可以向学生灌输极限的思想，极限是微积分中最主要、 最基本的概念，它从数量上描述变量在变化过程中的变化趋势，在高中数学中，极限思想渗 透到函数、数列等章节，又衔接高等数学，起着承上启下的作用. 2 2 OB 2 2 2 2 2 2 2 2 1 2 3 3 1 2 3 3 120 2π 60 π 2 2 60 π 3600 π