人教版九年级数学上册第23章复习课件 18页

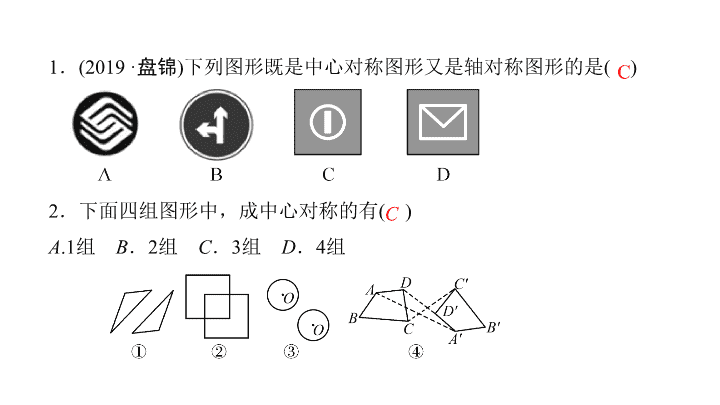
第二十三章　旋转 人教版 章末复习(三)　旋转 1 ． (2019 · 盘锦 ) 下列图形既是中心对称图形又是轴对称图形的是 ( ) 2 ．下面四组图形中，成中心对称的有 ( ) A .1 组 B ． 2 组 C ． 3 组 D ． 4 组 C C 3 ．关于某点成中心对称的两个图形，对应线段的关系是 ( ) A ．相等且在同一条直线上 B ．平行 C ．平行且相等 D ．相等、平行或在同一条直线上 D 4 ． ( 济宁中考 ) 如图，在平面直角坐标系中，点 A ， C 在 x 轴上， 点 C 的坐标为 ( － 1 ， 0) ， AC ＝ 2. 将 Rt △ABC 先绕点 C 顺时针旋转 90° ， 再向右平移 3 个单位长度，则变换后点 A 的对应点坐标是 ( ) A .(2 ， 2) B ． (1 ， 2) C ． ( － 1 ， 2) D ． (2 ，－ 1) A 5 ． (2019 · 滨州 ) 已知点 P(a － 3 ， 2 － a) 关于原点对称的点在第四象限， 则 a 的取值范围在数轴上表示正确的是 ( ) C 6 ． ( 济南中考 ) 如图，在平面直角坐标系中， △ ABC 的顶点都在方格线的格点上， 将△ ABC 绕点 P 顺时针方向旋转 90° ，得到△ A′B′C′ ， 则点 P 的坐标为 ( ) A ． (0 ， 4) B ． (1 ， 1) C ． (1 ， 2) D ． (2 ， 1) C 7 ． ( 济宁中考 ) 如图，在平面直角坐标系中，有一个 Rt △ABC ，且 A( － 1 ， 3) ， B( － 3 ，－ 1) ， C( － 3 ， 3) ，已知△ A 1 AC 1 是由△ ABC 旋转变换得到的． (1) 请写出旋转中心的坐标是 _______ ，旋转角是 ____ 度； (2) 以 (1) 中的旋转中心为中心， 分别画出△ A 1 AC 1 顺时针旋转 90° ， 180° 的三角形； (3) 设 Rt △ABC 两直角边 BC ＝ a ， AC ＝ b 、斜边 AB ＝ c ， 利用变换前后所形成的图案证明勾股定理． (0 ， 0) 90 8 ．如图，图②的图案是由图①中五种基本图形中的两种拼接而成， 这两种基本图形是 ( ) A .①② B ．①③ C ．①④ D ．③⑤ B 9 ．如图是一个 4×4 的正方形网格，每个小正方形的边长为 1. 请你在网格中以左上角的三角形为基本图形，通过平移、对称或旋转变换，设计一个精美图案，使其满足：①既是轴对称图形，又是以点 O 为对称中心的中心对称图形；②所作图案用阴影标识，且阴影部分面积为 4. 10 ．如图，把 △ ABC 绕点 C 按顺时针方向旋转 35° 得到 △ A′B′C ， A′B′ 交 AC 于点 D ，若 A′D ＝ CD ，则 ∠ A 的度数为 ( ) A ． 25° B ． 35° C ． 45° D ． 55° B D 12 ．如图，在等边三角形 ABC 中， AC ＝ 9 ，点 O 在 AC 上，且 AO ＝ 3 ， 点 P 在 AB 上，连接 OP ，将线段 OP 绕点 O 逆时针旋转 60° 得到线段 OD ， 要使点 D 恰好落在 BC 上，则 AP 的长为 ( ) A ． 5 B ． 6 C ． 7 D ． 8 B 13 ． ( 张家界中考 ) 如图，将△ ABC 绕点 A 逆时针旋转 150° ，得到△ ADE ，这时点 B ， C ， D 恰好在同一直线上，则∠ B 的度数为 ____ ． 15° 14 ．如图，在△ ABC 中，∠ BAC ＝ 120° ，以 BC 为边向外作等边△ BCD ， 把△ ABD 绕着点 D 按顺时针方向旋转 60° 到△ ECD 的位置， 若 AB ＝ 3 ， AC ＝ 2 ，求∠ BAD 的度数和 AD 的长． 解：由∠ BAC ＝ 120° 知∠ ABC ＋∠ ACB ＝ 60°. 又∵∠ ABD ＝∠ ABC ＋∠ CBD ＝∠ DCE ，∠ CBD ＝∠ BCD ＝ 60° ，∴∠ ACB ＋∠ BCD ＋∠ DCE ＝∠ ACB ＋∠ BCD ＋∠ ABC ＋∠ CBD ＝ 180° ，即点 A ， C ， E 在一条直线上．又∵ AD ＝ ED ，∠ ADE ＝ 60° ，∴△ ADE 为等边三角形．∴∠ BAD ＝∠ E ＝ 60° ， AD ＝ AE ＝ AC ＋ CE ＝ AC ＋ AB ＝ 5 【 核心素养 】 15 ． ( 类比探究 ) 如图①，在△ ABC 与△ ADE 中， AB ＝ AC ， AD ＝ AE ，∠ A 是公共角． (1)BD 与 CE 的数量关系是 BD____CE ； ( 填“ >”“<” 或“＝” ) (2) 把图①中的△ ABC 绕点 A 旋转一定的角度，得到如图②所示的图形， ①求证： BD ＝ CE ； ② BD 与 CE 所在直线的夹角与∠ DAE 的数量关系是什么？说明理由； (3) 若 AD ＝ 10 ， AB ＝ 6 ，把图①中的△ ABC 绕点 A 顺时针旋转 α 度 (0°<α≤360°) ，直接写出 BD 长度的取值范围． ＝ ② 结论： BD 与 CE 所在直线的夹角与∠ DAE 的度数相等．理由：延长 DB 交 CE 于点 F ，∵△ ABD≌△ACE ，∴∠ ADB ＝∠ AEC ，又∵∠ AOD ＝∠ EOF ，∴ 180° －∠ ADB －∠ AOD ＝ 180° －∠ AEC －∠ EOF ，即∠ DAE ＝∠ DFE (3)∵AD ＝ 10 ， AB ＝ 6 ，∴ AD － AB≤BD≤AD ＋ AB ，∴ 4≤BD≤16