2020年秋九年级数学上册 第4章 锐角三角函数 4 7页

第4章 　锐角三角形函数 ‎4.3　解直角三角形 知识点1　已知一边一角解直角三角形 ‎1．如图4－3－1，在Rt△ABC中，∠C＝90°.‎ ‎(1)已知∠A和c，则a＝________，b＝________；‎ ‎(2)已知∠B和b，则a＝________，c＝________．‎ ‎2．在直角三角形ABC中，已知∠C＝90°，∠A＝40°，BC＝3，则AC＝(　　)‎ A．3sin40° B．3sin50°‎ C．3tan40° D．3tan50°‎ 图4－3－1‎ ‎　　　‎ 图4－3－2‎ ‎3．如图4－3－2，在Rt△ABC中，∠C＝90°，∠B＝30°，AB＝8，则BC的长是(　　)‎ A. 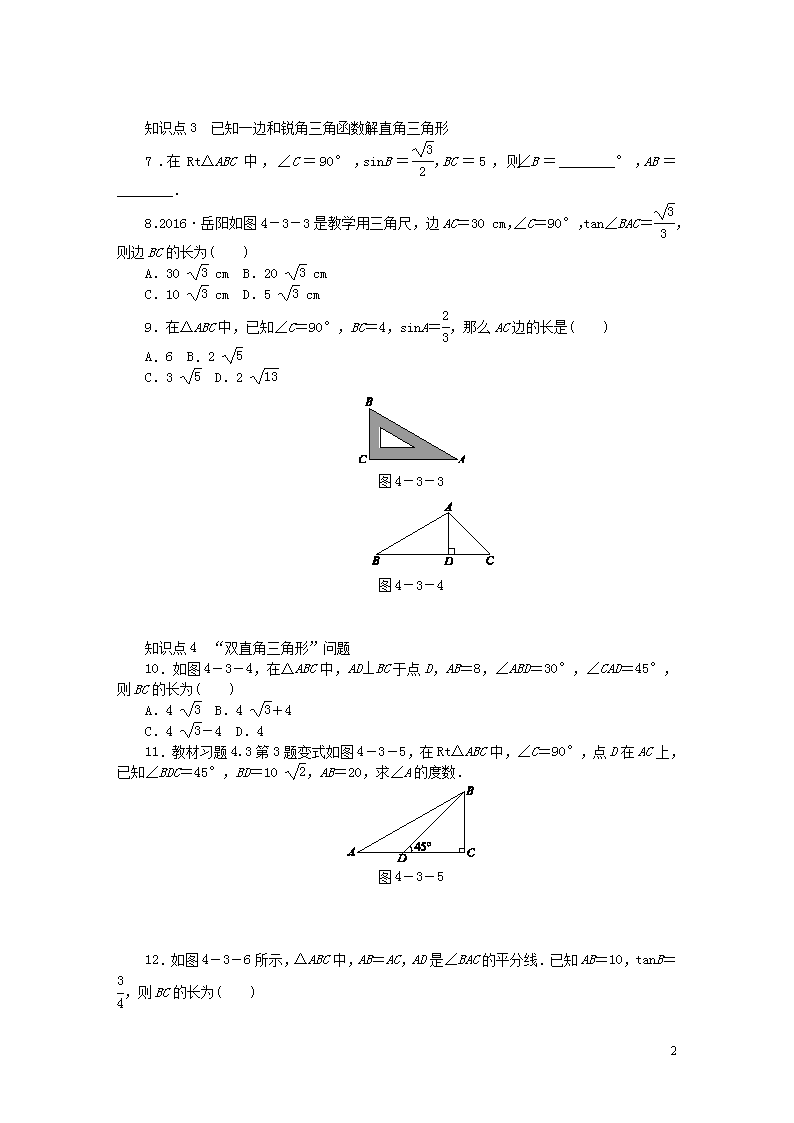B．‎4 C．8 D．4 ‎4．在Rt△ABC中，∠C＝90°，a＝8，∠B＝60°，求∠A，b，c.‎ 知识点2　已知两边解直角三角形 ‎5．已知在Rt△ABC中，∠C＝90°，BC＝，AC＝，则AB＝________，∠A＝______°，∠B＝________°.‎ ‎6．在Rt△ABC中，∠C＝90°，a，b，c分别是∠A，∠B，∠C的对边，如果a＝2，b＝2 ，求c及∠B.‎ 7‎ 知识点3　已知一边和锐角三角函数解直角三角形 ‎7．在Rt△ABC中，∠C＝90°，sinB＝，BC＝5，则∠B＝________°，AB＝________．‎ ‎8．2016·岳阳如图4－3－3是教学用三角尺，边AC＝‎30 cm，∠C＝90°，tan∠BAC＝，则边BC的长为(　　)‎ A．‎30 cm B．‎20 cm C．‎10 cm D．‎5 cm ‎9．在△ABC中，已知∠C＝90°，BC＝4，sinA＝，那么AC边的长是(　　)‎ A．6 B．2 C．3 D．2 图4－3－3‎ ‎　　　‎ 图4－3－4‎ 知识点4　“双直角三角形”问题 ‎10．如图4－3－4，在△ABC中，AD⊥BC于点D，AB＝8，∠ABD＝30°，∠CAD＝45°，则BC的长为(　　)‎ A．4 B．4 ＋4‎ C．4 －4 D．4‎ ‎11．教材习题4.3第3题变式如图4－3－5，在Rt△ABC中，∠C＝90°，点D在AC上，已知∠BDC＝45°，BD＝10 ，AB＝20，求∠A的度数．‎ 图4－3－5‎ ‎12．如图4－3－6所示，△ABC中，AB＝AC，AD是∠BAC的平分线．已知AB＝10，tanB＝，则BC的长为(　　)‎ 7‎ A．6 B．‎8 C．12 D．16‎ 图4－3－6‎ ‎　　　‎ 图4－3－7‎ ‎13．如图4－3－7，折叠矩形ABCD的一边AD，使点D落在BC边的点F处，已知AB＝‎8 cm，BC＝‎10 cm，则tan∠EAF＝________．‎ ‎14．如图4－3－8，在△ABC中，∠ABC＝90°，∠A＝30°，D是边AB上一点，∠BDC＝45°，AD＝4.求BC的长．(结果保留根号)‎ 图4－3－8‎ ‎15．如图4－3－9，在Rt△AOB中，∠AOB＝90°，OA＝2，OB＝1，OA与x轴的正方向的夹角为30°，求A，B两点的坐标．‎ 图4－3－9‎ ‎16．如图4－3－10，在四边形ABCD中，AD∥BC，∠ABC＝90°，∠BCD＝45°，点E在BC 7‎ 上，且∠AEB＝60°，若AB＝2 ，AD＝1，求CD和CE的长．(结果保留根号)‎ 图4－3－10‎ ‎ ‎ ‎17．如图4－3－11，已知Rt△ABC中，∠ACB＝90°，CD是斜边AB上的中线，过点A作AE⊥CD，AE与CD，CB分别相交于点H，E，AH＝2CH.‎ ‎(1)求sinB的值；‎ ‎(2)如果CD＝，求BE的长．‎ 图4－3－11‎ ‎　　　　‎ 详解详析 ‎1．(1)c·sinA　c·cosA ‎(2)　 ‎2．D　[解析] ∵∠C＝90°，∠A＝40°，‎ ‎∴∠B＝90°－∠A＝90°－40°＝50°.‎ 又∵tanB＝，∴AC＝BC·tanB＝3tan50°.‎ 7‎ 故选D.‎ ‎3．D　[解析] ∵在Rt△ABC中，∠C＝90°，∠B＝30°，AB＝8，cosB＝，即cos30°＝，‎ ‎∴BC＝8×＝4 .故选D.‎ ‎4．解：∠A＝90°－∠B＝30°，‎ c＝＝16，b＝a·tanB＝8 .‎ ‎5．2 　30　60‎ ‎6．解：在Rt△ABC中，由勾股定理，得 c2＝a2＋b2＝22＋(2 )2＝42，∴c＝4.‎ ‎∵sinB＝＝＝，∴∠B＝60°.‎ ‎7．60　10‎ ‎8．C　[解析] ∵在Rt△ABC中，∠C＝90°，‎ ‎∴tan∠BAC＝.‎ 又∵AC＝30 cm，tan∠BAC＝，‎ ‎∴BC＝AC·tan∠BAC＝30×＝10 (cm)．‎ 故选C.‎ ‎9．B　[解析] ∵在△ABC中，∠C＝90°，BC＝4，∴sinA＝＝＝，∴AB＝6，∴AC＝＝2 .‎ ‎10．B　[解析] 首先解Rt△ABD，求出AD，BD的长，再解Rt△ADC，求出DC的长，然后由BC＝BD＋DC即可求解．‎ ‎11．解：∵在Rt△BDC中，∠BDC＝45°，BD＝10 ，‎ ‎∴BC＝BD·sin∠BDC＝10 ×＝10.‎ ‎∵在Rt△ABC中，∠C＝90°，AB＝20，‎ ‎∴sinA＝＝＝，‎ ‎∴∠A＝30°.‎ ‎12．D　[解析] ∵AB＝AC，AD是∠BAC的平分线，∴AD⊥BC，BD＝CD，∴tanB＝＝，∴AD＝BD.∵AD2＋BD2＝AB2，‎ ‎∴(BD)2＋BD2＝102，∴BD＝8，∴BC＝16.故选D.‎ ‎13.　[解析] ∵四边形ABCD为矩形，∴CD＝AB＝‎8 cm，AD＝BC＝‎10 cm.‎ 7‎ ‎∵折叠矩形ABCD的一边AD，使点D落在BC边的点F处，‎ ‎∴AF＝AD＝‎10 cm，DE＝EF，∠AFE＝∠D＝90°.‎ 在Rt△ABF中，BF＝＝6 cm，‎ ‎∴FC＝BC－BF＝‎4 cm.‎ 设EF＝x cm，则DE＝x cm，CE＝CD－DE＝(8－x)cm.‎ 在Rt△CEF中，∵CF2＋CE2＝EF2，‎ ‎∴42＋＝x2，解得x＝5，即EF＝‎5 cm.在Rt△AEF中，tan∠EAF＝＝＝.‎ ‎14．解： 设BC＝x，在Rt△BCD中，∠DBC＝90°，∠BDC＝45°，∴BD＝BC＝x.‎ ‎∵AD＝4，∴AB＝4＋x.‎ 在Rt△ABC中，∠ABC＝90°，∠A＝30°，BC＝x，AB＝4＋x.‎ ‎∵tanA＝，即＝，解得x＝2 ＋2，‎ ‎∴BC的长为2 ＋2.‎ ‎15．解：过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D.‎ 在Rt△AOC中，AC＝2sin30°＝1，OC＝2cos30°＝，‎ 所以点A的坐标为(，1)．‎ 因为∠AOB＝90°，∠AOC＝30°，‎ 所以∠BOC＝60°.‎ 同理，BD＝OB·sin60°＝，OD＝OB·cos60°＝.‎ 因为点B在第四象限，‎ 所以点B的坐标为(，－)．‎ ‎16．解：过点D作DF⊥BC，垂足为F.‎ ‎∵AD∥BC，∠ABC＝90°，DF⊥BC，‎ ‎∴∠BAD＝∠ABC＝∠DFB＝90°，‎ ‎∴四边形ABFD为矩形，‎ ‎∴DF＝AB＝2 ，BF＝AD＝1.‎ ‎∵在Rt△DFC中，∠C＝45°，‎ ‎∴DF＝FC＝2 ，CD＝DF＝2 ，‎ ‎∴BC＝FC＋BF＝AB＋AD＝2 ＋1.‎ 在Rt△ABE中，BE＝＝2，‎ ‎∴CE＝BC－BE＝2 ＋1－2＝2 －1.‎ 即CD＝2 ，CE＝2 －1.‎ ‎17．解：(1)在Rt△ABC中，∵∠ACB＝90°，‎ ‎∴∠CAB＋∠B＝90°.‎ ‎∵AE⊥CD，‎ ‎∴∠CAH＋∠ACH＝90°.‎ ‎∵CD是斜边AB上的中线，∴CD＝AD，‎ ‎∴∠DAC＝∠ACD，∴∠B＝∠CAH，‎ ‎∴sinB＝sin∠CAH.‎ 又∵AH＝2CH，∴AC＝CH，‎ 7‎ ‎∴sinB＝sin∠CAH＝＝.‎ ‎(2)∵CD＝，∴AB＝2 .‎ ‎∵sinB＝，‎ ‎∴AC＝2，∴BC＝4.‎ 又∵sinB＝sin∠CAH＝＝，AC＝2，‎ ‎∴CE＝1，‎ ‎∴BE＝BC－CE＝4－1＝3.‎ 7‎