圆的对称性（第2课时）导学案 3页

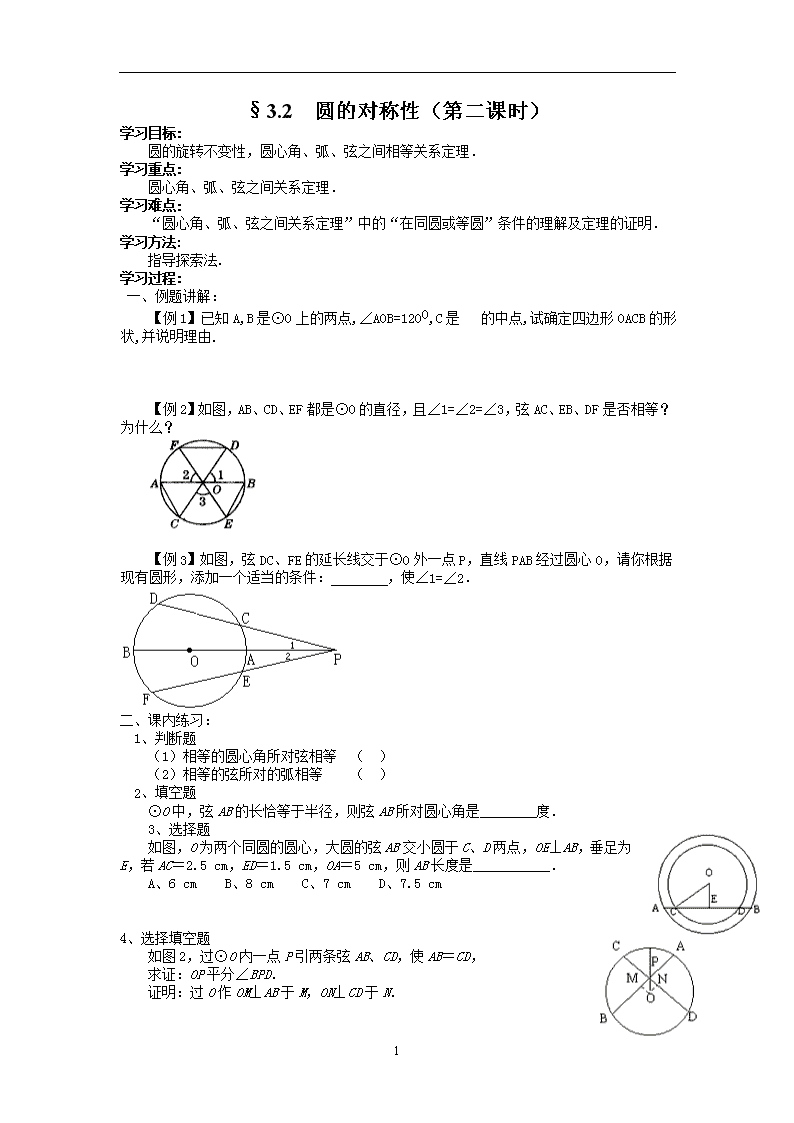
1 §3.2 圆的对称性（第二课时） 学习目标: 圆的旋转不变性，圆心角、弧、弦之间相等关系定理． 学习重点: 圆心角、弧、弦之间关系定理． 学习难点: “圆心角、弧、弦之间关系定理”中的“在同圆或等圆”条件的理解及定理的证明． 学习方法: 指导探索法. 学习过程: 一、例题讲解： 【例 1】已知 A,B 是⊙O 上的两点,∠AOB=1200,C 是 的中点,试确定四边形 OACB 的形 状,并说明理由. 【例 2】如图，AB、CD、EF 都是⊙O 的直径，且∠1=∠2=∠3，弦 AC、EB、DF 是否相等？ 为什么？ 【例 3】如图，弦 DC、FE 的延长线交于⊙O 外一点 P，直线 PAB 经过圆心 O，请你根据 现有圆形，添加一个适当的条件： ，使∠1=∠2． 二、课内练习： 　1、判断题 　　（1）相等的圆心角所对弦相等　（　） 　　（2）相等的弦所对的弧相等　　（　） 　2、填空题 　　⊙O 中，弦 AB 的长恰等于半径，则弦 AB 所对圆心角是________度． 　　3、选择题 　　如图，O 为两个同圆的圆心，大圆的弦 AB 交小圆于 C、D 两点，OE⊥AB，垂足为 E，若 AC＝2.5 cm，ED＝1.5 cm，OA＝5 cm，则 AB 长度是___________． 　　A、6 cm　　B、8 cm　　C、7 cm　　D、7.5 cm 　　 4、选择填空题 　　如图 2，过⊙O 内一点 P 引两条弦 AB、CD，使 AB＝CD， 　　求证：OP 平分∠BPD． 　　证明：过 O 作 OM⊥AB 于 M，ON⊥CD 于 N． 2 　　 A　OM⊥PB　　B　OM⊥AB　C　ON⊥CD　D　ON⊥PD 三、课后练习： 1．下列命题中，正确的有（ ） A．圆只有一条对称轴 B．圆的对称轴不止一条，但只有有限条 C．圆有无数条对称轴，每条直径都是它的对称轴 D．圆有无数条对称轴，经过圆心的每条直线都是它的对称轴 2．下列说法中，正确的是（ ） A．等弦所对的弧相等 B．等弧所对的弦相等 C．圆心角相等，所对的弦相等 D．弦相等所对的圆心角相等 3．下列命题中，不正确的是（ ） A．圆是轴对称图形 B．圆是中心对称图形 C．圆既是轴对称图形，又是中心对称图形 D．以上都不对 4．半径为 R 的圆中，垂直平分半径的弦长等于（ ） A． R B． R C． R D．2 R 5．如图 1，半圆的直径 AB=4，O 为圆心，半径 OE⊥AB，F 为 OE 的中点，CD∥AB，则弦 CD 的长为（ ） A．2 B． C． D．2 6．已知：如图 2，⊙O 的直径 CD 垂直于弦 AB，垂足为 P，且 AP=4cm，PD=2cm，则⊙O 的半径为（ ） A．4cm B．5cm C．4 cm D．2 cm 7．如图 3，同心圆中，大圆的弦 AB 交小圆于 C、D，已知 AB=4，CD=2，AB 的弦心距等 于 1，那么两个同心圆的半径之比为（ ） A．3：2 B． ：2 C． ： D．5：4 8．半径为 R 的⊙O 中，弦 AB=2R，弦 CD=R，若两弦的弦心距分别为 OE、OF，则 OE：OF= （ ） A．2：1 B．3：2 C．2：3 D．0 9．在⊙O 中，圆心角∠AOB=90°，点 O 到弦 AB 的距离为 4，则⊙O 的直径的长为（ ） A．4 B．8 C．24 D．16 10．如果两条弦相等，那么（ ） A．这两条弦所对的弧相等 B．这两条弦所对的圆心角相等 C．这两条弦的弦心距相等 D．以上答案都不对 11．⊙O 中若直径为 25cm，弦 AB 的弦心距为 10cm，则弦 AB 的长为 ． 12．若圆的半径为 2cm，圆中的一条弦长 2 cm，则此弦中点到此弦所对劣弧的中点 的距离为 ． 13．AB 为圆 O 的直径，弦 CD⊥AB 于 E，且 CD=6cm，OE=4cm，则 AB= ． 4 3 2 3 3 3 3 3 5 5 2 3 5 5 2 2 2 3 3 14．半径为 5 的⊙O 内有一点 P，且 OP=4，则过点 P 的最短的弦长是 ，最长的 弦长是 ． 15．弓形的弦长 6cm，高为 1cm，则弓形所在圆的半径为 cm． 16．在半径为 6cm 的圆中，垂直平分半径的弦长为 cm． 17．一条弦把圆分成 1：3 两部分，则弦所对的圆心角为 ． 18．弦心距是弦的一半时，弦与直径的比是 ，弦所对的圆心角是 ． 19．如图 4，AB、CD 是⊙O 的直径 OE⊥AB，OF⊥CD，则∠EOD ∠BOF， ，AC AE． 20．如图 5，AB 为⊙O 的弦，P 是 AB 上一点，AB=10cm，OP=5cm，PA=4cm，求⊙O 的半 径． 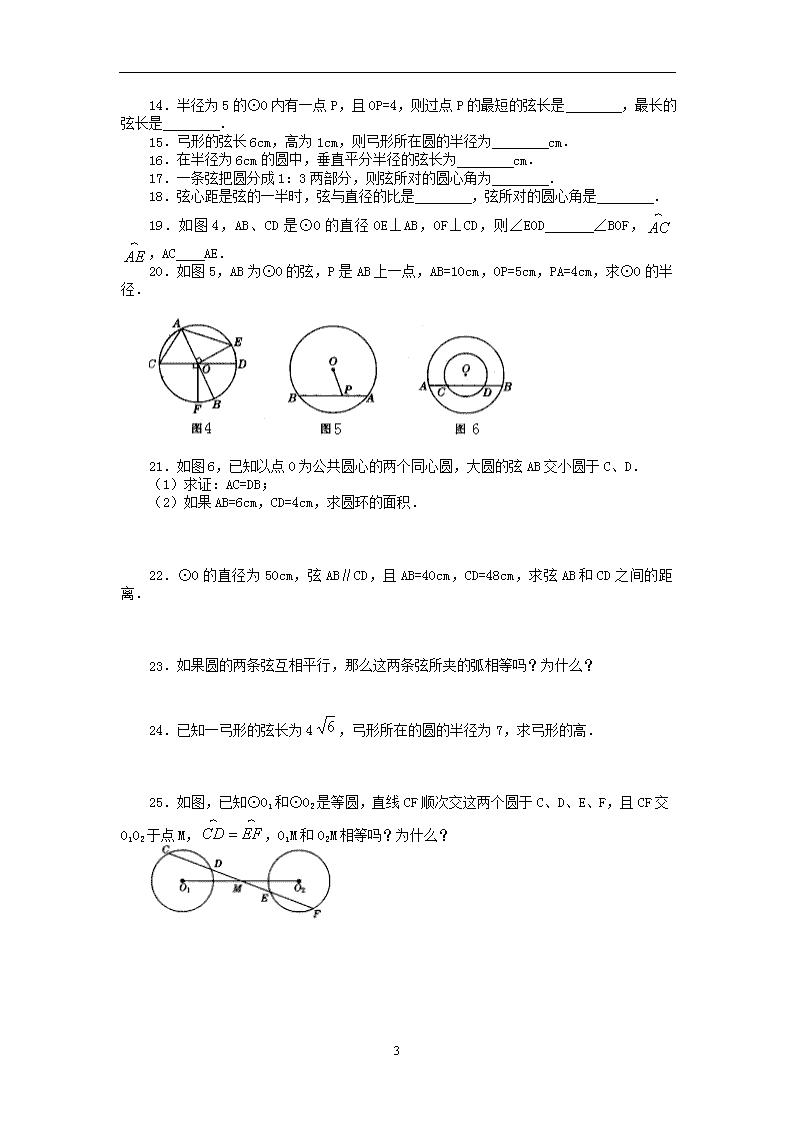21．如图 6，已知以点 O 为公共圆心的两个同心圆，大圆的弦 AB 交小圆于 C、D． （1）求证：AC=DB； （2）如果 AB=6cm，CD=4cm，求圆环的面积． 22．⊙O 的直径为 50cm，弦 AB∥CD，且 AB=40cm，CD=48cm，求弦 AB 和 CD 之间的距 离． 23．如果圆的两条弦互相平行，那么这两条弦所夹的弧相等吗？为什么？ 24．已知一弓形的弦长为 4 ，弓形所在的圆的半径为 7，求弓形的高． 25．如图，已知⊙O1 和⊙O2 是等圆，直线 CF 顺次交这两个圆于 C、D、E、F，且 CF 交 O1O2 于点 M， ，O1M 和 O2M 相等吗？为什么？ ⌒ AC ⌒ AE 6 ⌒⌒ EFCD =