北师大版数学九年级上册同步课件-1第一章-1正方形的判定 19页

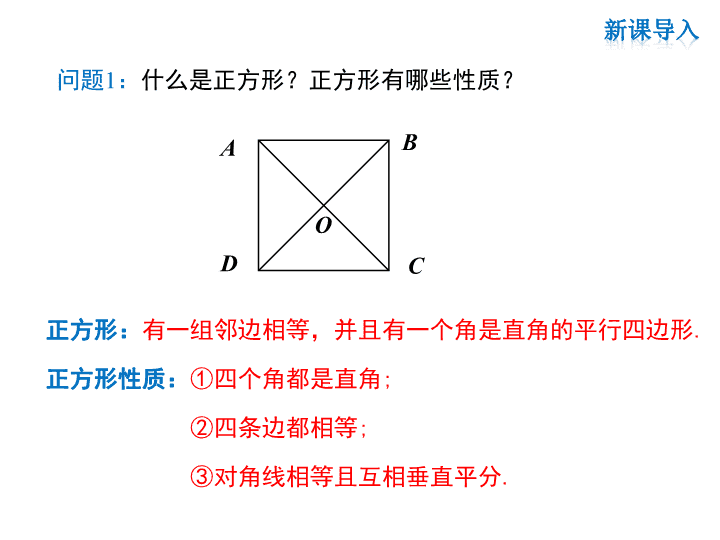
第一章特殊平行四边形1.3正方形的性质与判定第2课时正方形的判定 1．掌握正方形的判定方法．（重点）2．会运用正方形的判定条件进行有关的论证和计算.(难点)学习目标 问题1：什么是正方形？正方形有哪些性质？ABCD正方形：有一组邻边相等，并且有一个角是直角的平行四边形.正方形性质：①四个角都是直角;②四条边都相等;③对角线相等且互相垂直平分.O新课导入 问题2：你是如何判断是矩形、菱形？平行四边形矩形菱形四边形三个角是直角四条边相等定义三个判定定理定义对角线相等定义对角线垂直新课导入 正方形判定的定理作一作：过点A作射线AM的垂线AN,分别在AM,AN上取点B,D,使AB=AD,作DC∥AB,BC∥AD,得四边形ABCD.AMNBDC问题1：上面所画四边形ABCD是正方形吗？为什么？新课讲解1 想一想：将矩形纸片对折两次，怎样裁剪才能使剪下的三角形展开后是个正方形？（1）（2）（3）（4）新课讲解 菱形问题2：满足怎样条件的矩形是正方形？矩形正方形一组邻边相等对角线互相垂直问题3：满足怎样条件的菱形是正方形？正方形一个角是直角对角线相等新课讲解 1.对角线相等的菱形是正方形.2.对角线垂直的矩形是正方形.3.有一个角是直角的菱形是正方形.正方形判定的两条途径：正方形正方形++先判定菱形先判定矩形矩形条件菱形条件(1)(2)一个直角对角线相等一组邻边相等对角线垂直新课讲解定理： 如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证：四边形BECF是正方形.FABECD解析：先由两组平行线得出四边形BECF平行四边形；再由一个直角，得出是矩形；最后由一组邻边相等可得正方形.45°45°新课讲解正方形判定定理的应用2例1 FABECD证明:∵BF∥CE,CF∥BE，∴四边形BECF是平行四边形.∵四边形ABCD是矩形,∴∠ABC=90°,∠DCB=90°,∵BE平分∠ABC,CE平分∠DCB,∴∠EBC=45°,∠ECB=45°,∴∠EBC=∠ECB.∴EB=EC,∴□BECF是菱形.在△EBC中,∵∠EBC=45°,∠ECB=45°,∴∠BEC=90°,∴菱形BECF是正方形.新课讲解 已知：如图所示,在Rt△ABC中,∠C=90°,∠BAC,∠ABC的平分线于点D,DE⊥BC于点E,DF⊥AC于点F.求证：四边形CEDF是正方形.证明:如图所示,过点D作DG⊥AB于点G.∵DF⊥AC,DE⊥BC,∴∠DFC=∠DEC=90°.又∠C=90°,∴四边形CEDF是矩形（有三个角是直角的四边形是矩形）.∵AD平分∠BAC,DF⊥AC,DG⊥AB.∴DF=DG.同理可得DE=DG,∴DE=DF.∴四边形CEDF是正方形（有一组邻边相等的矩形是正方形）.CEBAFDG新课讲解例2 如图，EG,FH过正方形ABCD的对角线的交点O,且EG⊥FH.求证：四边形EFGH是正方形.证明：∵四边形ABCD为正方形,∴OB=OC,∠ABO=∠BCO=45°,∠BOC=90°=∠COH+∠BOH.∵EG⊥FH,∴∠BOE+∠BOH=90°,∴∠COH=∠BOE,∴△CHO≌△BEO,∴OE=OH.同理可证：OE=OF=OG,BACDOEHGF新课讲解例3 ∴OE=OF=OG=OH.又∵EG⊥FH,∴四边形EFGH为菱形.∵EO+GO=FO+HO,即EG=HF,∴四边形EFGH为正方形.BACDOEHGF新课讲解 做一做：顺次连接任意四边形各边中点所得的四边形是平行四边形.顺次连接矩形、正方形各边中点能得到怎样的特殊平行四边形？ABCDABCDABCD矩形正方形任意四边形平行四边形菱形正方形EFGHEFGHEFGH中点四边形新课讲解3 常见中点四边形比较总结归纳 1.下列命题正确的是（）A.四个角都相等的四边形是正方形B.四条边都相等的四边形是正方形C.对角线相等的平行四边形是正方形D.对角线互相垂直的矩形是正方形2．四个内角都相等的四边形一定是（）A.正方形B.菱形C.矩形D.平行四边形DC随堂练习 3.如图，在四边形ABCD中,AB=BC,对角线BD平分ABC,P是BD上一点,过点P作PMAD,PNCD,垂足分别为M、N.(1)求证：ADB=CDB;(2)若ADC=90,求证：四边形MPND是正方形.CABDPMN证明：（1）∵AB=BC,BD平分∠ABC.∴∠1=∠2.∴△ABD≌△CBD(AAS).∴∠ADB=∠CDB.12随堂练习 CABDPMN（2）∵∠ADC=90°;又∵PM⊥AD,PN⊥CD;∴∠PMD=∠PND=90°.∴四边形NPMD是矩形.∵∠ADB=∠CDB;∴∠ADB=∠CDB=45°.∴∠MPD=∠NPD=45°.∴DM=PM,DN=PN.∴四边形NPMD是正方形.随堂练习 有一个角是90°（或对角线互相垂直）有一对邻边相等（或对角线相等）平行四边形矩形菱形正方形一组邻边相等且一个内角为直角（或对角线互相垂直平分且相等）有一个角是90°（或对角线互相垂直）有一对邻边相等（或对角线相等）课堂总结