北师大版数学九年级上册同步练习课件-《特殊平行四边形》复习与巩固 27页

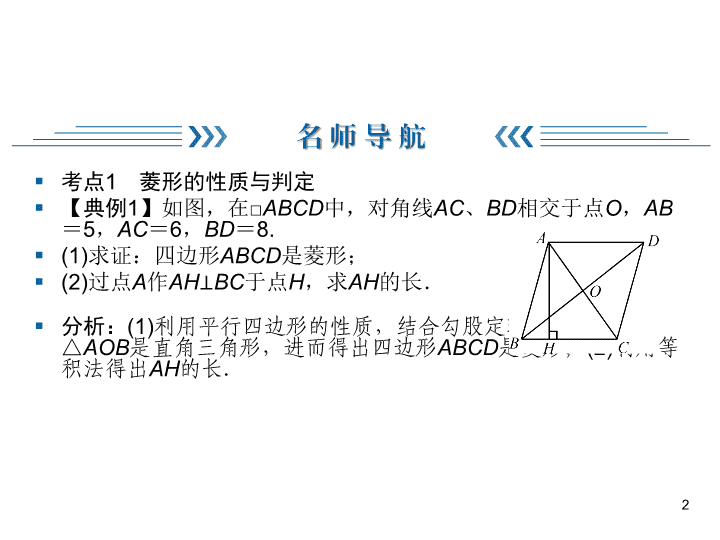
第一章　特殊平行四边形《特殊平行四边形》复习与巩固 考点1菱形的性质与判定【典例1】如图，在□ABCD中，对角线AC、BD相交于点O，AB＝5，AC＝6，BD＝8.(1)求证：四边形ABCD是菱形；(2)过点A作AH⊥BC于点H，求AH的长．分析：(1)利用平行四边形的性质，结合勾股定理的逆定理得出△AOB是直角三角形，进而得出四边形ABCD是菱形；(2)利用等积法得出AH的长．2名师导航 3 4 考点2矩形的性质与判定【典例2】如图，在矩形ABCD中，AB＝24cm，BC＝8cm，点P从A开始沿折线A－B－C－D以4cm/s的速度移动，点Q从C开始沿CD边以2cm/s的速度移动，如果点P、Q分别从A、C同时出发，当其中一点到达D时，另一点也随之停止运动，设运动时间为ts．当t为何值时，四边形QPBC为矩形？分析：根据题意，得CQ＝2tcm，AP＝4tcm，则BP＝(24－4t)cm.又∠B＝∠C＝90°，CD∥AB，则CQ＝BP时，四边形QPBC是矩形，得出方程2t＝24－4t，解方程即可．5 解答：根据题意，得CQ＝2tcm，AP＝4tcm，则BP＝(24－4t)cm.∵四边形ABCD是矩形，∴∠B＝∠C＝90°，CD∥AB，∴当CQ＝BP时，四边形QPBC是矩形，即2t＝24－4t，解得t＝4.故当t＝4时，四边形QPBC是矩形．6 考点3正方形的性质与判定【典例3】如图，□ABCD中，对角线AC、BD相交于点O，且AC⊥BD，请你添加一个适当的条件________，使□ABCD成为正方形．7分析：∵□ABCD的对角线AC、BD相交于点O，且AC⊥BD，∴□ABCD为菱形，∴根据有一个角是直角的菱形是正方形，可以添加条件：∠BAD＝90°，此时□ABCD为正方形．答案：∠BAD＝90°(答案不唯一) 点评：本题利用三角形的面积巧妙建立所求线段与已知线段的关系，从而解决问题．8 考点4中点四边形【典例5】如果点K、L、M、N分别是四边形ABCD的四条边AB、BC、CD、DA的中点，且四边形KLMN是矩形，那么下列选项正确的是()A．AB⊥BCB．AC⊥BDC．AB＝BCD．AC＝BD分析：由题知，矩形KLMN是四边形ABCD的中点四边形，∴四边形ABCD的对角线互相垂直，∴AC⊥BD.答案：B9 ★考点1菱形的性质与判定1．【山东聊城中考】如图，△ABC中，DE∥BC，EF∥AB，要判定四边形DBFE是菱形，还需要添加的条件是()A．AB＝ACB．AD＝BDC．BE⊥ACD．BE平分∠ABC10考点专练D 2．菱形OACB在平面直角坐标系中的位置如图所示，点C的坐标是(6,0)，点A的纵坐标是1，则点B的坐标是()A．(3,1)B．(3，－1)C．(1，－3)D．(1,3)3．在菱形ABCD中，∠A＝30°，在同一平面内，以对角线BD为底边作顶角为120°的等腰三角形BDE，则∠EBC的度数为________________.11B45°或105° 12 5．如图，四边形ABCD是轴对称图形，且直线AC是对称轴，AB∥CD，则下列结论：①AC⊥BD；②AD∥BC；③四边形ABCD是菱形；④△ABD≌△CDB.其中正确的是____________.(只填写序号)13①②③④ 6．如图，已知点E、F分别是□ABCD的边BC、AD的中点，且∠BAC＝90°.(1)求证：四边形AECF是菱形；(2)若∠B＝30°，BC＝10，求菱形AECF的面积．14 15 ★考点2矩形的性质与判定1．在等腰△ABC中，AB＝AC，延长BA到点D，延长CA到点E，使AD＝AB，AE＝AC，连接CD、DE、EB，则四边形BCDE的形状是__________，其依据是_____________________________.16矩形对角线相等的平行四边形是矩形2．【辽宁辽阳中考】如图，在矩形ABCD中，∠ABC的平分线交AD于点E，连接CE.若BC＝7，AE＝4，则CE＝_________.5 3．平行四边形ABCD中，过点D作DE⊥AB于点E，点F在CD上，CF＝AE，连接BF、AF.(1)求证：四边形BFDE是矩形；(2)若AF平分∠BAD，且AE＝3，DE＝4，求矩形BFDE的面积．17 18 19C 2．如图，在正方形ABCD中，连接BD，点O是BD的中点，若M、N是边AD上的两点，连接MO、NO，并分别延长交边BC于点M′、N′，则图中的全等三角形共有()A．2对B．3对C．4对D．5对20C 2122.5 5．【山东青岛中考】已知：如图，在菱形ABCD中，点E、O、F分别为AB、AC、AD的中点，连接CE、CF、OE、OF.(1)求证：△BCE≌△DCF；(2)当AB与BC满足什么关系时，四边形AEOF是正方形？请说明理由．22 23 24 25 ★考点4中点四边形1．顺次连接一个四边形的各边中点，得到一个矩形，则下列四边形中满足条件的是()①平行四边形；②菱形；③矩形；④对角线互相垂直的四边形．A．①③B．②③C．③④D．②④26D 2．如图，连接四边形ABCD各边中点，得到四边形EFGH，只要添加条件_____________，就能保证四边形EFGH是菱形．3．如图，已知E、F、G、H分别为菱形ABCD四边的中点，AB＝6cm，∠ABC＝60°，则四边形EFGH的面积为__________cm2.27AC＝BD