北师大版八年级数学上册期末复习测试卷（有答案） 20页

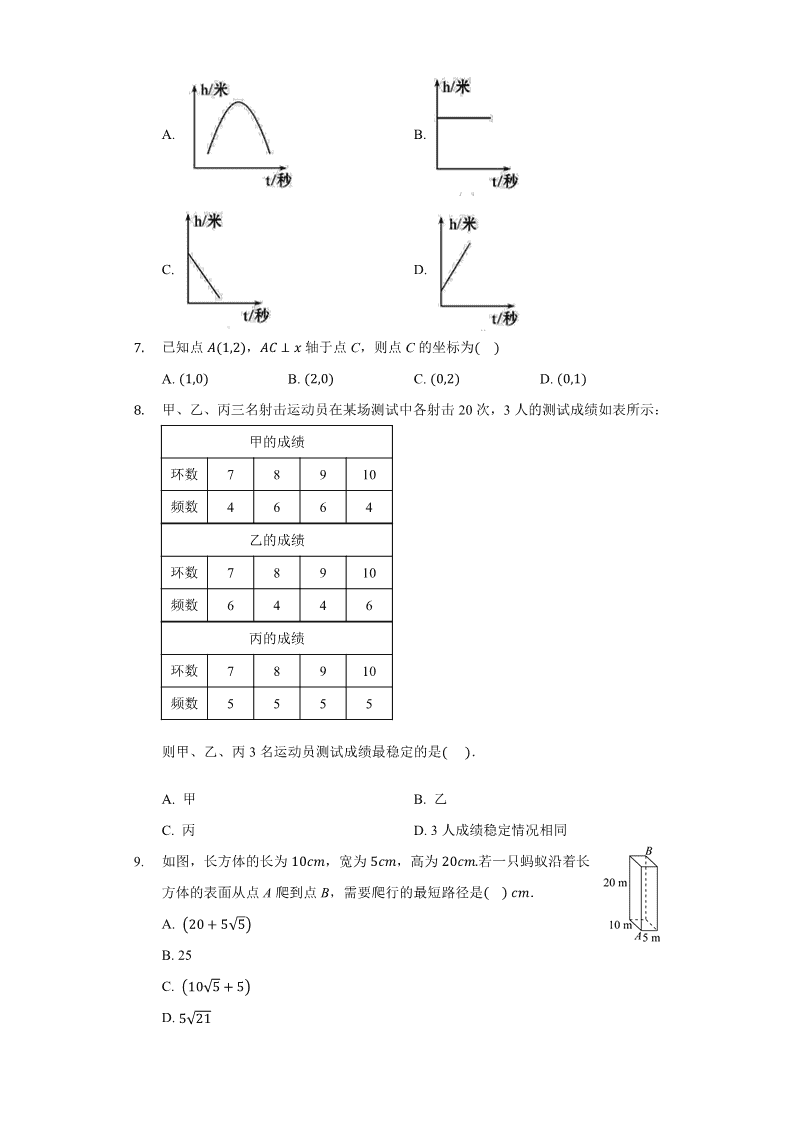
北师大版八年级数学上册期末复习测试卷题号一二三四总分得分一、选择题（本大题共10小题，共30分）1.如图，issa，点E在线段BC上，若ᦙ䁡⸶，ᦙ⸶，则1的度数是A.⸶B.⸶C.⸶D.⸶.关于的叙述，正确的是A.是有理数B.5的平方根是C.D.在数轴上不能找到表示的点.如图，数轴上点A表示的数是2，点B表示的数是，且iᦙa，则点C表示的数是A.B.C.D..若一个数的算术平方根等于它本身，则这个数是．A.1B.1C.0D.0或1.下列说法中错误的是A.要了解某种灯管的使用寿命，一般采用抽样调查B.一组数据的方差越小，这组数据的稳定性越差C.数据1、2、3、4的中位数是.D.数据3，4，5，6，6的众数是6.周一的升旗仪式上，同学们看到匀速上升的旗子，能反映其高度与时间关系的图象大致是 A.B.C.D.䁡.已知点1，a轴于点C，则点C的坐标为A.1⸶B.⸶C.⸶D.⸶18.甲、乙、丙三名射击运动员在某场测试中各射击20次，3人的测试成绩如表所示：甲的成绩环数78910频数4664乙的成绩环数78910频数6446丙的成绩环数78910频数5555则甲、乙、丙3名运动员测试成绩最稳定的是．A.甲B.乙C.丙D.3人成绩稳定情况相同9.如图，长方体的长为1⸶䁚，宽为䁚，高为⸶䁚.若一只蚂蚁沿着长方体的表面从点A爬到点B，需要爬行的最短路径是䁚．A.⸶䁢B.25C.1⸶䁢D.1 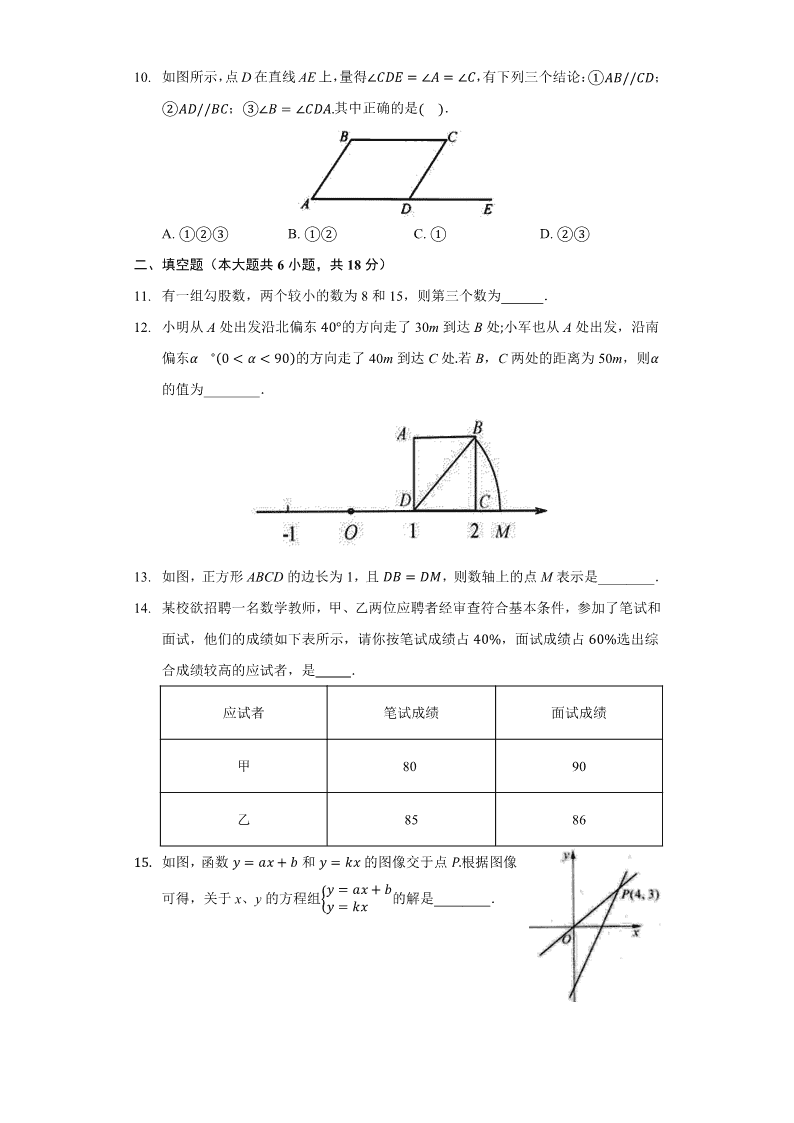10.如图所示，点D在直线AE上，量得aᦙᦙa，有下列三个结论：issa；ssia；iᦙa.其中正确的是．A.B.C.D.二、填空题（本大题共6小题，共18分）11.有一组勾股数，两个较小的数为8和15，则第三个数为______．12.小明从A处出发沿北偏东⸶的方向走了30m到达B处小军也从A处出发，沿南偏东⸶㌳⸶的方向走了40m到达C处.若B，C两处的距离为50m，则的值为________．13.如图，正方形ABCD的边长为1，且iᦙ，则数轴上的点M表示是________．14.某校欲招聘一名数学教师，甲、乙两位应聘者经审查符合基本条件，参加了笔试和面试，他们的成绩如下表所示，请你按笔试成绩占⸶，面试成绩占⸶选出综合成绩较高的应试者，是．应试者笔试成绩面试成绩甲8090乙85861.如图，函数ᦙ䁢฀和ᦙ㐶的图像交于点.根据图像ᦙ䁢฀可得，关于x、y的方程组的解是________．ᦙ㐶 1.如图，点F在ia的平分线AP上，点E在AB上，且′ssa，若i′ᦙ⸶，则′ᦙ________．三、计算题（本大题共1小题，共6分）1䁡.计算䁢䁢䁢四、解答题（本大题共8小题，共64分）18.阅读材料：我们知道，䁢ᦙ䁢1ᦙ，类似地，我们把䁢฀看成一个整体，则䁢฀䁢฀䁢䁢฀ᦙ䁢1䁢฀ᦙ䁢฀.“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛尝试应用1把฀看成一个整体，合并฀฀䁢฀的结果是______；已知ᦙ，求1的值______．1㌳.如图是台阶的一部分，已知在某一平面直角坐标系内点A的坐标为⸶⸶.点B的坐标为11．1请在图中画出该平面直角坐标系．并写出其余各点的坐标；说明点B，C，D，E，F的坐标与点A的坐标相比有什么变化； 现要给台阶铺上地毯，单位长度为1，请你算一算要多长的地毯．20.如图所示，在ABC中，ACᦙ8，BCᦙ，在ABE中，DE为AB上的高，DEᦙ1，ABEᦙ⸶，求ABC的面积．21.如图，BD是ia的角平分线，BD交AC于点D，ssia，交AB于点E，ᦙ，iaᦙ⸶．1求a的度数；求i的度数． 22.某校分甲、乙两组举办了一次诗歌朗诵比赛，计分采用10分制，选手得分均为整数，成绩达到9分以上为优秀．这次比赛中甲、乙两组学生成绩分布的条形统计图如下．1补充完成下列的成绩统计分析表：组别平均分中位数众数方差优秀率甲组8分1.⸶乙组8分8分1.⸶甲组同学说他们组的优秀率均高于乙组，所以他们组的成绩好于乙组，但乙组同学不同意甲组同学的说法，认为他们组的成绩要好于甲组，请你给出一条支持乙组同学观点的理由．23.团结奋战，众志成城，齐齐哈尔市组织援助医疗队，分别乘甲、乙两车同时出发，沿同一路线赶往绥芬河．齐齐哈尔距绥芬河的路程为800km，在行驶过程中乙车速度始终保持8⸶㐶s，甲车先以一定速度行驶了500km，用时5h，然后再以乙车的速度行驶，直至到达绥芬河加油、休息时间忽略不计.甲、乙两车离齐齐哈尔的路程㐶与所用时间的关系如图所示，请结合图象解答下列问题：1甲车改变速度前的速度是______㐶s，乙车行驶______h到达绥芬河； 求甲车改变速度后离齐齐哈尔的路程㐶与所用时间之间的函数解析式，不用写出自变量x的取值范围；甲车到达绥芬河时，乙车距绥芬河的路程还有______km；出发______h时，甲、乙两车第一次相距40km．24.如图，点i⸶฀，点⸶分别在y轴、x轴正半轴上，且满足฀䁢฀1ᦙ⸶．1求A、B两点的坐标，i的度数；如图1，已知⸶1，在第一象限内存在点G，HG交AB于E，使BE为i䁨的中线，且iᦙ，求点E到BH的距离． 25.学校准备假期组织老师去隆中参加诸葛亮文化节，现有甲、乙两家旅行社表示对老师优惠.设参加文化节的老师有x人，甲、乙两家旅行社实际收费分别为1元，元，且它们的函数图象如图所示，根据图象信息，请你回答下列问题：1当参加老师的人数为多少时，两家旅行社收费相同？分别求出1，关于x的函数关系式？如果共有50人参加时，选择哪家旅行社合算？ 答案和解析1.【答案】B【解析】【分析】先根据三角形外角的性质求出a的度数，再由平行线的性质即可得出结论．本题考查了平行线的性质．【解答】ᦙ䁡⸶，ᦙ⸶，且是a的外角．aᦙᦙ⸶．issa．1ᦙaᦙ⸶．故选B．2.【答案】C【解析】解：A、是无理数，故说法错误；B、5的平方根应是，故说法错误；C、，说法正确；D、在数轴上能找到表示的点，故说法错误；故选：C．根据无限不循环小数是无理数可得A说法错误，根据平方根的定义可得5的平方根是可得B说法错误，根据㌳可得C说法正确；根据实数与数轴上点是一一对应关系可得D说法错误．此题主要考查了实数，以及平方根，关键是掌握实数与数轴上点是一一对应关系，掌握正数有两个平方根，它们互为相反数．3.【答案】C【解析】 【分析】本题考查实数与数轴，两点间的距离，解答本题的关键是明确题意，求出点C表示的数，利用数形结合的思想解答，根据题意可以列出相应的等式，从而可以解答本题．【解答】解：设点C表示的数为c，数轴上A、B两点表示的数分别为2和，且iᦙa，ᦙ䁚，解得䁚ᦙ，故选C．4.【答案】D【解析】【分析】本题考查了算术平方根的定义，掌握算术平方根的定义是解决问题的关键.根据算术平方根的定义即可求解．【解答】解：若一个数的算术平方根等于它本身，则这个数是0或1，故选D．5.【答案】B【解析】解：A、要了解某种灯管的使用寿命，一般采用抽样调查，正确；B、一组数据的方差越大，这组数据的稳定性越差，故错误；C、数据1、2、3、4的中位数是.，正确；D、数据3，4，5，6，6的众数是6，正确，故选：B．利用调查方式的选择、方差、众数及中位数的定义分别判断即可确定正确的答案．本题考查了调查方式的选择、方差、众数及中位数的定义，属于统计基础题，比较简单．6.【答案】D【解析】【分析】本题考查了函数图象，根据旗子匀速上升可知，高度与时间的关系是一次函数关系，且 随着时间的增大高度在逐渐增大，然后根据各选项图象选择即可．【解答】解：旗子是匀速上升的，且开始时是拿在同学手中，旗子的高度与时间关系是一次函数关系，并且随着时间的增大高度在不断增大，纵观各选项，只有D选项图象符合．故选D．7.【答案】A【解析】【分析】本题考查了坐标与图形性质：利用点的坐标求相应线段的长和判断线段与坐标轴的位置关系.由于a轴，则点C与点A的横坐标相同，然后利用x轴上点的坐标特征即可得到C点坐标．【解答】解：a轴于点C，而1，a1⸶．故选A.8.【答案】A【解析】【分析】本题考查了方差的定义与意义：一般地设n个数据，1，，的平均数为，则方差1ᦙ1䁢䁢䁢，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立.根据题意，分别计算出甲乙丙三个人的方差可得，甲的方差小于乙、丙的方差，结合方差的意义，可得甲最稳定．【解答】解：甲的平均数ᦙ䁡䁢8䁢㌳䁢1⸶⸶ᦙ8.，乙的平均数ᦙ䁡䁢8䁢㌳䁢1⸶⸶ᦙ8.，丙的平均数ᦙ䁡䁢8䁢㌳䁢1⸶⸶ᦙ8.， ᦙ䁡8.䁢88.䁢㌳8.䁢1⸶1⸶8.⸶ᦙ甲1.⸶，ᦙ䁡8.䁢88.䁢㌳8.䁢1⸶8.⸶ᦙ1.，乙ᦙ䁡8.䁢88.䁢㌳8.䁢1⸶8.⸶ᦙ1.，丙，甲丙乙甲的成绩最稳定．故选A．9.【答案】B【解析】【分析】本题考查了勾股定理的拓展应用．“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.作此题要把这个长方体中，蚂蚁所走的路线放到一个平面内，在平面内线段最短，根据勾股定理即可计算．【解答】解：第一种情况：把我们所看到的左面和上面组成一个平面，则这个长方形的长和宽分别是10cm和25cm，则所走的最短线段是1⸶䁢ᦙ㌳䁚；第二种情况：把我们看到的前面与上面组成一个长方形，则这个长方形的长和宽分别是30cm和5cm，所以走的最短线段是⸶䁢ᦙ䁡䁚；第三种情况：把我们所看到的前面和右面组成一个长方形，则这个长方形的长和宽分别是15cm和20cm，所以走的最短线段是1䁢⸶ᦙ䁚；三种情况比较而言，第三种情况最短．故选B．10.【答案】A【解析】【分析】本题考查了平行线的性质和判定的应用，主要考查学生的推理能力． 根据平行线的判定推出ssia，issa，根据平行线的性质得出i䁢ᦙ18⸶，䁢aᦙ18⸶，即可得出答案．【解答】解：aᦙa，ssia内错角相等，两直线平行，故正确；ᦙa，issa同位角相等，两直线平行，故正确；i䁢ᦙ18⸶，䁢aᦙ18⸶，iᦙa等量代换，故正确；即正确的结论有，故选：A．11.【答案】17【解析】解：设第三个数为为正整数，由题意得：ᦙ8䁢1，解得：ᦙ1䁡，故答案为：17．根据勾股数：满足䁢฀ᦙ䁚的三个正整数，称为勾股数可设第三个数为为正整数，由题意得：ᦙ8䁢1，再解方程即可．此题主要考查了勾股数，关键是掌握勾股数：满足䁢฀ᦙ䁚的三个正整数．12.【答案】50【解析】【分析】本题考查了勾股定理的逆定理的应用．根据勾股定理的逆定理得到iaᦙ㌳⸶，根据角的和差即可得到结论．【解答】解：iᦙ⸶，aᦙ⸶，iaᦙ⸶，i䁢aᦙia，iaᦙ㌳⸶，ᦙ㌳⸶⸶ᦙ⸶，ᦙ⸶， 故答案为：50．13.【答案】䁢1【解析】【分析】本题考查了实数与数轴，利用勾股定理得出DM的长是解题关键．根据勾股定理，可得DM的长，根据线段的和差，可得答案．【解答】解：由勾股定理，得ᦙiᦙ，数轴上的点M表示的数是䁢1，故答案为䁢1．14.【答案】甲【解析】【分析】本题考查加权平均数，关键是掌握加权平均数计算公式，根据题意先算出甲、乙两人的加权平均数，再进行比较，即可得出答案．【解答】解：甲的得分ᦙ8⸶⸶䁢㌳⸶⸶ᦙ8，乙的得分ᦙ8⸶䁢8⸶ᦙ8.，故选甲．ᦙ15.【答案】ᦙ【解析】【分析】此题考查了一次函数与二元一次方程组的关系，方程组的解就是使方程组中两个方程同时成立的一对未知数的值，而这一对未知数的值也同时满足两个相应的一次函数式，因此方程组的解就是两个相应的一次函数图象的交点坐标．由图可知：两个一次函数的交点坐标为；那么交点坐标同时满足两个函数的解析式，而所求的方程组正好是由两个函数的解析式所构成，因此两函数的交点坐标即为方程组的解．【解答】解：函数ᦙ䁢฀和ᦙ㐶的图象交于点， 即ᦙ，ᦙ同时满足两个一次函数的解析式，ᦙ䁢฀ᦙ所以关于x，y的方程组的解是．ᦙ㐶ᦙᦙ故答案为．ᦙ16.【答案】20【解析】【分析】本题考查平行线的性质，角的平分线的有关知识，属于基础题．根据平行线的性质得到ia的度数，然后利用角平分线的定义求出a的度数，再利用平行线的性质求解即可．【解答】解：′ssa，i′ᦙ⸶，iaᦙi′ᦙ⸶，点F在ia的平分线AP上，11aᦙiaᦙ⸶ᦙ⸶，′ssa，′ᦙaᦙ⸶．故答案为20．17.【答案】解：原式ᦙ䁢䁢䁢ᦙ䁢ᦙ䁢䁢ᦙ䁢．【解析】本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可.在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．首先根据平方差公式及完全平方公式将原式展开，最后根据实数运算法则进行计算即可．18.【答案】1฀；㌳．【解析】 【分析】本题主要考查了整式的加减，解决问题的关键是运用整体思想；给出整式中字母的值，求整式的值的问题，一般要先化简，再把给定字母的值代入计算，得出整式的值，不能把数值直接代入整式中计算．1把฀看成一个整体，运用合并同类项法则进行计算即可；把1变形，得到1，再根据整体代入法进行计算即可．【解答】解：1把฀看成一个整体，则฀฀䁢฀ᦙ䁢฀ᦙ฀；ᦙ，原式ᦙ1ᦙ11ᦙ㌳．故答案为฀；㌳．19.【答案】解：1如图，a，，，′；点B，C，D，E，F的坐标与点A的坐标相比，横坐标与纵坐标依次增加1；台阶的横向长度为6，纵向长度为5，地毯的长度为11个单位长度．【解析】本题主要考查平面直角坐标系，能根据题意画出正确的平面直角坐标系是解此题的关键.根据平面直角坐标系内点A的坐标为⸶⸶，点B的坐标为11可知平面直角坐标系的坐标原点为点A．120.【答案】解：ᦙ1，iᦙiᦙ⸶，iᦙ1⸶．aᦙ8，iaᦙ，䁢8ᦙ1⸶，a䁢iaᦙi，由勾股定理逆定理得aᦙ㌳⸶． 11iaᦙaiaᦙ8ᦙ．【解析】本题主要考查了三角形的面积公式和勾股定理的逆定理，熟练掌握三角形的面积公式和勾股定理的逆定理是解题的关键．由iᦙ⸶，求得iᦙ1⸶，根据勾股定理的逆定理得出ia为直角三角形，从而得到ia的面积．21.【答案】解：1iaᦙi䁢，iᦙiaᦙ1．i平分ia，iaᦙiᦙ⸶．䁢ia䁢aᦙ18⸶，aᦙ18⸶iaᦙ1⸶．ssia，ᦙiaᦙ⸶．i䁢ᦙ18⸶，iᦙ18⸶ᦙ1⸶．【解析】本题考查三角形的内角和定理、平行线的性质、角平分线的定义等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．1根据三角形内角和定理即可解决问题；求出，利用邻补角的性质即可解决问题．22.【答案】解：18分；7分和9分；8分.；因为甲乙两组学生成绩的平均分相等，而乙组学生的方差低于甲组学生的方差，说明乙组学生成绩的波动性比甲组小，所以乙组学生的成绩好于甲组．【解析】【分析】本题考查的是条形统计图的综合运用．读懂统计图，从统计图中得到必要的信息是解决问题的关键． 1首先根据条形统计图，分别得到两组的成绩，然后根据中位数的定义求出甲组的中位数，利用加权平均数求出乙组的平均分；需先根据统计图，再结合它们的优秀率、方差等，说出乙组优于甲组的情况即可，因为乙组学生的方差低于于甲组学生，所以乙组学生的成绩好于甲组。【解答】解：1根据条形图可得，两小组各有10人，甲组的成绩为：6分的1人，7分的3人，8分的2人，9分的3人，10分的1人，乙组的成绩为：6分的1人，7分的2人，8分的4人，9分的2人，10分的1人，甲组的中位数为：8分，众数为7分和9分1䁢䁡䁢8䁢㌳䁢1⸶1乙组的平均分为：ᦙ8分，1⸶故答案为8分；7分和9分；8分．见答案．23.【答案】100101002【解析】解：1甲车改变速度前的速度为：500出ᦙ1⸶⸶㐶s，乙车达绥芬河是时间为：8⸶⸶8⸶ᦙ1⸶，故答案为：100；10；乙车速度为8⸶㐶s，8⸶⸶⸶⸶甲车到达绥芬河的时间为：䁢ᦙ，8⸶甲车改变速度后，到达绥芬河前，设所求函数解析式为：ᦙ㐶䁢฀㐶⸶，㐶䁢฀ᦙ⸶⸶将⸶⸶和8⸶⸶代入得：，㐶䁢฀ᦙ8⸶⸶㐶ᦙ8⸶解得，฀ᦙ1⸶⸶ᦙ8⸶䁢1⸶⸶，答：甲车改变速度后离齐齐哈尔的路程㐶与所用时间之间的函数解析式为ᦙ8⸶䁢1⸶⸶；甲车到达绥芬河时，乙车距绥芬河的路程为：8⸶⸶8⸶ᦙ1⸶⸶㐶，⸶1⸶⸶8⸶ᦙ，即出发2h时，甲、乙两车第一次相距40km． 故答案为：100；2．1结合图象，根据“速度ᦙ路程时间”即可得出甲车改变速度前的速度；根据“时间ᦙ路程速度”即可得出乙车行驶的时间；根据题意求出甲车到达绥芬河的时间，再根据待定系数法解答即可；根据甲车到达绥芬河的时间即可求出甲车到达绥芬河时，乙车距绥芬河的路程；根据“路程差ᦙ速度差时间”列式计算即可得出甲、乙两车第一次相距40km行驶的时间．本题考查一次函数的应用，利用待定系数法求一次函数的解析式，运用数形结合的方法是解答本题的关键．24.【答案】解：1฀䁢฀1ᦙ⸶，฀1ᦙ⸶，且฀ᦙ⸶，点i⸶฀，点⸶分别在y轴、x轴正半轴上，฀⸶，ᦙ฀ᦙ，⸶，i⸶，ᦙiᦙ，iᦙ；⸶1，iᦙ1ᦙ，1设点E到BH的距离为h，则iᦙi，1ᦙ，解得ᦙ，即点E到BH的距离为2．【解析】1根据非负数的性质可求得a、b的值，则可求得A、B两点的坐标，则可求得ᦙi，可求得i；由H、B的坐标可求得BH，利用i的面积可求得点E到BH的距离．本题主要考查非负数的性质及三角形的面积，在1中利用非负数的性质求得a、b的值是解题的关键，在中利用三角形的面积公式得到关于h的方程是解题的关键．25.【答案】解：1由图象可得，当参加老师的人数为30时，两家旅行社收费相同；设1关于x的函数关系式是1ᦙ， ⸶ᦙ18⸶⸶，得ᦙ⸶，即1关于x的函数关系式是1ᦙ⸶；设关于x的函数关系式是ᦙ㐶䁢฀，฀ᦙ⸶⸶，⸶㐶䁢฀ᦙ18⸶⸶㐶ᦙ⸶解得，฀ᦙ⸶⸶即关于x的函数关系式是ᦙ⸶䁢⸶⸶；当ᦙ⸶时，1ᦙ⸶⸶ᦙ⸶⸶⸶，ᦙ⸶⸶䁢⸶⸶ᦙ⸶⸶，因为1，所以选择乙家旅行社．【解析】本题考查一次函数的应用、方案选择问题，解答本题的关键是明确题意，利用一次函数的性质和数形结合的思想解答．1根据函数图象和图象中的数据可以得到当参加老师的人数为多少时，两家旅行社收费相同；根据函数图象中的数据可以求得1、关于x的函数关系式；根据ᦙ⸶时，代入函数解析式计算比较即可．