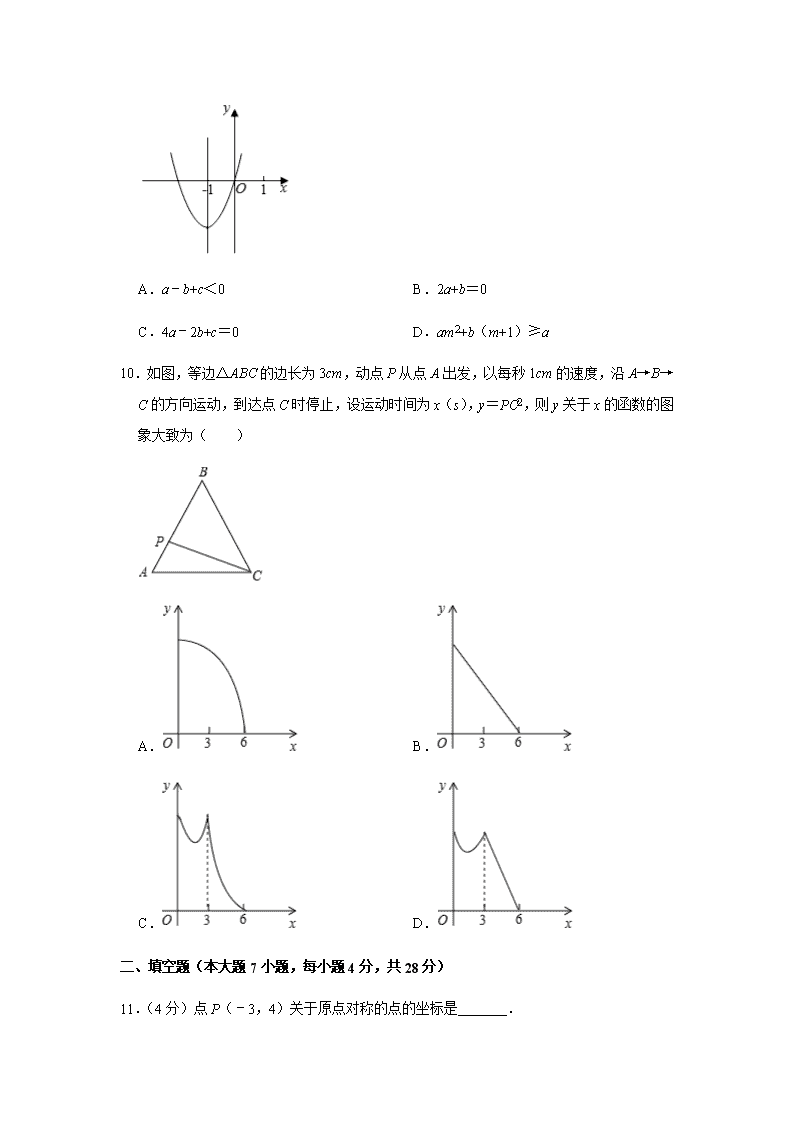2020-2021学年广东省汕头市金园实验中学九年级（上）期中数学试卷 解析版 32页

2020-2021学年广东省汕头市金园实验中学九年级（上）期中数学试卷一、选择题（本大题10小题，每小题3分，共30分）1．下列标志中，可以看作是中心对称图形的是（　　）A．B．C．D．2．用配方法解方程x2﹣4x+2＝0，配方正确的是（　　）A．（x+2）2＝2B．（x﹣2）2＝2C．（x﹣2）2＝﹣2D．（x﹣2）2＝63．如图，在Rt△ABC中，∠BAC＝90°，将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′，点A在边B′C上，则∠B′的大小为（　　）A．42°B．48°C．52°D．58°4．将抛物线y＝2（x﹣4）2﹣1先向左平移4个单位长度，再向上平移2个单位长度，平移后所得抛物线的解析式为（　　）A．y＝2x2+1B．y＝2x2﹣3C．y＝2（x﹣8）2+1D．y＝2（x﹣8）2﹣35．如图，四边形PAOB是扇形OMN的内接矩形，顶点P在上，且不与M，N重合，当 P点在上移动时，矩形PAOB的形状、大小随之变化，则AB的长度（　　）A．变大B．变小C．不变D．不能确定6．若一个二次函数y＝ax2+bx+c（a＞0）的图象经过五个点A（﹣1，n）、B（3，n）、C（2，y1）、D（﹣1，y2）和E（1，y3），则下列关系正确的是（　　）A．y1＞y2＞y3B．y2＞y1＞y3C．y1＜y3＜y2D．y3＞y1＞y27．如图，已知在⊙O中，点A，B，C均在圆上，∠AOB＝80°，则∠ACB等于（　　）A．130°B．140°C．145°D．150°8．若x支球队参加篮球比赛，共比赛了36场，每2队之间都比赛一场，则下列方程中符合题意的是（　　）A．x（x﹣1）＝36B．x（x+1）＝36C．x（x﹣1）＝36D．x（x+1）＝369．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，对称轴是直线x＝﹣1，则下列四个结论错误的是（　　） A．a﹣b+c＜0B．2a+b＝0C．4a﹣2b+c＝0D．am2+b（m+1）≥a10．如图，等边△ABC的边长为3cm，动点P从点A出发，以每秒1cm的速度，沿A→B→C的方向运动，到达点C时停止，设运动时间为x（s），y＝PC2，则y关于x的函数的图象大致为（　　）A．B．C．D．二、填空题（本大题7小题，每小题4分，共28分）11．（4分）点P（﹣3，4）关于原点对称的点的坐标是　　． 12．（4分）一元二次方程x2＝x的根　　．13．（4分）已知函数y＝（k﹣3）x2+2x+1的图象与x轴有交点，则k的取值范围为　　．14．（4分）设a、b是方程x2+x﹣2018＝0的两个不等的实根，则a2+2a+b的值为　　．15．（4分）如图，在⊙O中，AB是直径，弦AE的垂直平分线交⊙O于点C，CD⊥AB于D，BD＝1，AE＝4，则AD的长为　　．16．（4分）如图，边长为1的正方形ABCD，将正方形ABCD绕顶点A顺时针旋转45°得到正方形AB′C′D′，则图中阴影部分的面积为　　．17．（4分）如图，一段抛物线：y＝﹣x（x﹣2）（0≤x≤2）记为C1，它与x轴交于两点O，A1；将C1绕A1旋转180°得到C2，交x轴于A2；将C2绕A2旋转180°得到C3，交x轴于A3；…如此进行下去，直至得到C6，若点P（11，m）在第6段抛物线C6上，则m＝　　． 三、解答题（一）（本大题3小题，每小题6分，共18分）18．（6分）解方程：．19．（6分）已知抛物线y＝x2﹣（m﹣3）x﹣m．（1）求证：无论m取何值时，抛物线都与x轴有两个交点．（2）m为何值时，抛物线都与x轴有两个交点间的距离等于3？20．（6分）如图，抛物线y＝x2+bx+c经过坐标原点，并与x轴交于点A（2，0）．（1）求此抛物线的解析式；（2）写出顶点坐标及对称轴；（3）若抛物线上有一点B，且S△OAB＝3，求点B的坐标．四、解答题（二）（本大题3小题，每小题7分，共21分）21．（7分）如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，坐标分别为A（2，2），B（1，0），C（3，1）．（1）画出△ABC关于y轴对称的△A1B1C1； （2）画出将△ABC绕原点O顺时针旋转90°所得的△A2B2C2；（3）△A1B1C1与△A2B2C2成中心对称图形吗？若成中心对称图形，直接写出对称中心的坐标．22．（7分）如图，在⊙O中，点C、D在优弧上，将弧沿BC折叠后，点D的对应点E刚好落在弦AB上，连接AC、EC．（1）证明：AC＝EC；（2）连接AD，若CE＝5，AD＝8，求⊙O的半径．23．（7分）如图，是400米跑道示意图，中间的足球场ABCD是矩形，两边是半圆，直道AB的长是多少？你一定知道是100米!可你也许不知道，这不仅仅为了比赛的需要，还有另外一个原因，等你做完本题就明白了．设AB＝x米．（1）请用含x的代数式表示BC． （2）设矩形ABCD的面积为S．①求出S关于x的函数表达式．②当直道AB为多少米时，矩形ABCD的面积最大？五、解答题（三）（本大题2小题，每小题10分，共20分）24．（10分）如图，点E是正方形ABCD的边BC上一点，连接DE，将DE绕着点E逆时针旋转90°，得到EG，过点G作GF⊥CB，垂足为F，GH⊥AB，垂足为H，连接DG，交AB于I．（1）求证：四边形BFGH是正方形；（2）求证：ED平分∠CEI；（3）连接IE，若正方形ABCD的边长为3，则△BEI的周长为　　．25．（10分）如图，抛物线L：y＝ax2+bx+c与x轴交于A、B（3，0）两点（A在B的左侧），与y轴交于点C（0，3），已知对称轴x＝1．（1）求抛物线L的解析式；（2）将抛物线L向下平移h个单位长度，使平移后所得抛物线的顶点落在△OBC内（包括△OBC的边界），求h的取值范围；（3）设点P是抛物线L上任一点，点Q在直线l：x＝﹣3上，△PBQ能否成为以点P为直角顶点的等腰直角三角形？若能，求出符合条件的点P 的坐标；若不能，请说明理由． 2020-2021学年广东省汕头市金园实验中学九年级（上）期中数学试卷参考答案与试题解析一、选择题（本大题10小题，每小题3分，共30分）1．下列标志中，可以看作是中心对称图形的是（　　）A．B．C．D．【分析】根据中心对称图形的概念：把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，由此结合各图形的特点求解．【解答】解：根据中心对称的定义可得：A、C、D都不符合中心对称的定义．故选：B．2．用配方法解方程x2﹣4x+2＝0，配方正确的是（　　）A．（x+2）2＝2B．（x﹣2）2＝2C．（x﹣2）2＝﹣2D．（x﹣2）2＝6【分析】根据一元二次方程的配方法即可求出答案．【解答】解：∵x2﹣4x+2＝0，∴x2﹣4x+4＝2，∴（x﹣2）2＝2，故选：B． 3．如图，在Rt△ABC中，∠BAC＝90°，将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′，点A在边B′C上，则∠B′的大小为（　　）A．42°B．48°C．52°D．58°【分析】先根据旋转的性质得出∠A′＝∠BAC＝90°，∠ACA′＝48°，然后在直角△A′CB′中利用直角三角形两锐角互余求出∠B′＝90°﹣∠ACA′＝42°．【解答】解：∵在Rt△ABC中，∠BAC＝90°，将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′，∴∠A′＝∠BAC＝90°，∠ACA′＝48°，∴∠B′＝90°﹣∠ACA′＝42°．故选：A．4．将抛物线y＝2（x﹣4）2﹣1先向左平移4个单位长度，再向上平移2个单位长度，平移后所得抛物线的解析式为（　　）A．y＝2x2+1B．y＝2x2﹣3C．y＝2（x﹣8）2+1D．y＝2（x﹣8）2﹣3【分析】根据平移的规律即可得到平移后函数解析式．【解答】解：抛物线y＝2（x﹣4）2﹣1先向左平移4个单位长度，得到的抛物线解析式为y＝2（x﹣4+4）2﹣1，即y＝2x2﹣1，再向上平移2个单位长度得到的抛物线解析式为y＝2x2﹣1+2，即y＝2x2+1；故选：A．5．如图，四边形PAOB是扇形OMN的内接矩形，顶点P在上，且不与M，N重合，当P点在上移动时，矩形PAOB的形状、大小随之变化，则AB的长度（　　） A．变大B．变小C．不变D．不能确定【分析】PAOB是扇形OMN的内接矩形，根据矩形的性质AB＝OP＝半径，所以AB长度不变．【解答】解：∵PAOB是扇形OMN的内接矩形，∴AB＝OP＝半径，当P点在上移动时，半径一定，所以AB长度不变，故选：C．6．若一个二次函数y＝ax2+bx+c（a＞0）的图象经过五个点A（﹣1，n）、B（3，n）、C（2，y1）、D（﹣1，y2）和E（1，y3），则下列关系正确的是（　　）A．y1＞y2＞y3B．y2＞y1＞y3C．y1＜y3＜y2D．y3＞y1＞y2【分析】由A，B两点的纵坐标相同，可得A，B两点关于对称轴对称，可求对称轴为直线x＝1，则x＝1时y3值最小，根据二次函数的图象性质：在对称轴的左侧，y随x的增大而减小．【解答】解：∵A（﹣1，n）、B（3，n），∴对称轴为直线x＝1；∵a＞0，∴x＝1时，y3是最小值；∵C（2，y1）关于对称轴的对称点为（0，y1），且﹣1＜0＜1，∴y2＞y1＞y3．故选：B． 7．如图，已知在⊙O中，点A，B，C均在圆上，∠AOB＝80°，则∠ACB等于（　　）A．130°B．140°C．145°D．150°【分析】设点E是优弧AB上的一点，连接EA，EB，根据同弧所对的圆周角是圆心角的一半可求得∠E的度数，再根据圆内接四边形的对角互补即可得到∠ACB的度数．【解答】解：设点E是优弧AB上的一点，连接EA，EB∵∠AOB＝80°∴∠E＝∠AOB＝40°∴∠ACB＝180°﹣∠E＝140°．故选：B．8．若x支球队参加篮球比赛，共比赛了36场，每2队之间都比赛一场，则下列方程中符合题意的是（　　）A．x（x﹣1）＝36B．x（x+1）＝36C．x（x﹣1）＝36D．x（x+1）＝36【分析】根据题意可以列出相应的方程，本题得以解决．【解答】解：由题意可得， ＝36，故选：A．9．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，对称轴是直线x＝﹣1，则下列四个结论错误的是（　　）A．a﹣b+c＜0B．2a+b＝0C．4a﹣2b+c＝0D．am2+b（m+1）≥a【分析】根据二次函数的图象与系数的关系即可求解．【解答】解：由抛物线可得当x＝﹣1时，y＜0，故a﹣b+c＜0，故结论A正确；抛物线可得对称轴为x＝﹣＝﹣1，故2a﹣b＝0，故结论B错误．由抛物线经过原点，对称轴为直线x＝﹣1可知，当x＝﹣2时，y＝0，故4a﹣2b+c＝0，故结论C正确；当x＝﹣1时，该函数取得最小值，则am2+bm+c≥a﹣b+c，即am2+b（m+1）≥a，故结论D正确；故选：B．10．如图，等边△ABC的边长为3cm，动点P从点A出发，以每秒1cm的速度，沿A→B→C的方向运动，到达点C时停止，设运动时间为x（s），y＝PC2，则y关于x的函数的图象大致为（　　） A．B．C．D．【分析】需要分类讨论：①当0≤x≤3，即点P在线段AB上时，根据余弦定理知cosA＝，所以将相关线段的长度代入该等式，即可求得y与x的函数关系式，然后根据函数关系式确定该函数的图象．②当3＜x≤6，即点P在线段BC上时，y与x的函数关系式是y＝（6﹣x）2＝（x﹣6）2（3＜x≤6），根据该函数关系式可以确定该函数的图象．【解答】解：∵正△ABC的边长为3cm，∴∠A＝∠B＝∠C＝60°，AC＝3cm．①当0≤x≤3时，即点P在线段AB上时，AP＝xcm（0≤x≤3）；根据余弦定理知cosA＝， 即＝，解得，y＝x2﹣3x+9（0≤x≤3）；该函数图象是开口向上的抛物线；解法二：过C作CD⊥AB，则AD＝1.5cm，CD＝cm，点P在AB上时，AP＝xcm，PD＝|1.5﹣x|cm，∴y＝PC2＝（）2+（1.5﹣x）2＝x2﹣3x+9（0≤x≤3）该函数图象是开口向上的抛物线；②当3＜x≤6时，即点P在线段BC上时，PC＝（6﹣x）cm（3＜x≤6）；则y＝（6﹣x）2＝（x﹣6）2（3＜x≤6），∴该函数的图象是在3＜x≤6上的抛物线；故选：C．二、填空题（本大题7小题，每小题4分，共28分）11．（4分）点P（﹣3，4）关于原点对称的点的坐标是　（3，﹣4）　．【分析】本题比较容易，考查平面直角坐标系中任意一点P（x，y），关于原点的对称点是（﹣x，﹣y），即关于原点的对称点，横纵坐标都变成相反数．【解答】解：根据中心对称的性质，得点P （﹣3，4）关于原点对称的点的坐标是（3，﹣4）．12．（4分）一元二次方程x2＝x的根　x1＝0，x2＝1　．【分析】先移项，然后利用提取公因式法对等式的左边进行因式分解．【解答】解：由原方程得x2﹣x＝0，整理得x（x﹣1）＝0，则x＝0或x﹣1＝0，解得x1＝0，x2＝1．故答案是：x1＝0，x2＝1．13．（4分）已知函数y＝（k﹣3）x2+2x+1的图象与x轴有交点，则k的取值范围为　k≤4　．【分析】分为两种情况：①当k﹣3≠0时，（k﹣3）x2+2x+1＝0，求出△＝b2﹣4ac＝﹣4k+16≥0的解集即可；②当k﹣3＝0时，得到一次函数y＝2x+1，与X轴有交点；即可得到答案．【解答】解：①当k﹣3≠0时，（k﹣3）x2+2x+1＝0，△＝b2﹣4ac＝22﹣4（k﹣3）×1＝﹣4k+16≥0，k≤4；②当k﹣3＝0时，y＝2x+1，与x轴有交点；故k的取值范围是k≤4，故答案为：k≤4．14．（4分）设a、b是方程x2+x﹣2018＝0的两个不等的实根，则a2+2a+b的值为　2017　．【分析】由根与系数的关系及一元二次方程的解可得出a2+a＝2018，a+b＝﹣1，将其代入a2+2a+b＝a2+a+（a+b）中即可求出结论． 【解答】解：∵a，b是方程x2+x﹣2018＝0的两个不等的实根，∴a2+a＝2018，a+b＝﹣1，∴a2+2a+b＝a2+a+（a+b）＝2018﹣1＝2017．故答案为：2017．15．（4分）如图，在⊙O中，AB是直径，弦AE的垂直平分线交⊙O于点C，CD⊥AB于D，BD＝1，AE＝4，则AD的长为　4　．【分析】证明△AOF≌△COD（AAS），得CD＝AF＝2，设⊙O的半径为r，则OD＝r﹣1，根据勾股定理列方程可得结论．【解答】解：弦AE的垂直平分线交AE于点F，∴AF＝AE＝2，∠AFO＝90°，∵CD⊥AB，∴∠ODC＝∠AFO＝90°，∵OA＝OC，∠AOF＝∠COD，∴△AOF≌△COD（AAS），∴CD＝AF＝2，设⊙O的半径为r，则OD＝r﹣1，由勾股定理得：OC2＝OD2+CD2，r2＝（r﹣1）2+22， r＝，∴AD＝AB﹣1＝2×﹣1＝4，故答案为：4．16．（4分）如图，边长为1的正方形ABCD，将正方形ABCD绕顶点A顺时针旋转45°得到正方形AB′C′D′，则图中阴影部分的面积为　﹣1　．【分析】连接AC，根据旋转的性质和正方形的性质得出∠D′AC′＝∠D′AB′＝45°，AD′＝D′C′＝AD＝AB′＝1，∠ABC＝∠D′＝90°，求出A、B、C′三点共线，根据勾股定理得求出AC′长，求出B′C′和BE，再分别求出△AD′C′和△EBC′的面积，再求出答案即可．【解答】解：连接AC′， ∵边长为1的正方形ABCD，将正方形ABCD绕顶点A顺时针旋转45°得到正方形AB′C′D′，∴AD′＝D′C′＝AD＝AB＝1，∠ABC＝∠D′＝90°，∠D′C′A＝45°，∠D′AC′＝45°，∠D′AB＝45°，∴A、B、C′三点共线，在Rt△AD′C′中，由勾股定理得：AC′＝＝＝，∴BC′＝AC′﹣AB＝﹣1，∵在Rt△EBC′中，∠EBC′＝90°，∠EC′B′＝45°，∴∠BEC′＝∠EC′B＝45°，∴EB＝BC′＝﹣1，∴阴影部分的面积S＝△AD′C′的面积﹣△EBC′的面积＝﹣＝﹣（﹣1）×（﹣1）＝﹣1，故答案为：﹣1．17．（4分）如图，一段抛物线：y＝﹣x（x﹣2）（0≤x≤2）记为C1，它与x轴交于两点O，A1；将C1绕A1旋转180°得到C2，交x轴于A2；将C2绕A2旋转180°得到C3，交x轴于A3；…如此进行下去，直至得到C6，若点P（11，m）在第6段抛物线C6上，则m＝　﹣1　． 【分析】将这段抛物线C1通过配方法求出顶点坐标及抛物线与x轴的交点，由旋转的性质可以知道C1与C2的顶点到x轴的距离相等，且OA1＝A1A2，照此类推可以推导知道点P（11，m）为抛物线C6的顶点，从而得到结果．【解答】解：∵y＝﹣x（x﹣2）（0≤x≤2），∴配方可得y＝﹣（x﹣1）2+1（0≤x≤2），∴顶点坐标为（1，1），∴A1坐标为（2，0）∵C2由C1旋转得到，∴OA1＝A1A2，即C2顶点坐标为（3，﹣1），A2（4，0）；照此类推可得，C3顶点坐标为（5，1），A3（6，0）；C4顶点坐标为（7，﹣1），A4（8，0）；C5顶点坐标为（9，1），A5（10，0）；C6顶点坐标为（11，﹣1），A6（12，0）；∴m＝﹣1．故答案为：﹣1．三、解答题（一）（本大题3小题，每小题6分，共18分）18．（6分）解方程：．【分析】利用因式分解法求解即可．【解答】解：∵（x﹣3）2＝2x﹣6，∴（x﹣3）2﹣2（x﹣3）＝0，则（x﹣3）（x﹣7）＝0，∴x﹣3＝0或x﹣7＝0， 解得x1＝3，x2＝7．19．（6分）已知抛物线y＝x2﹣（m﹣3）x﹣m．（1）求证：无论m取何值时，抛物线都与x轴有两个交点．（2）m为何值时，抛物线都与x轴有两个交点间的距离等于3？【分析】（1）求抛物线解析式的判别式，利用配方法判断△＞0即可；（2）根据抛物线与x轴的两个交点间的距离得到＝3，然后解方程即可．【解答】解：（1）证明：∵△＝（m﹣3）2﹣4（﹣m）＝（m﹣1）2+8＞0，∴抛物线与x轴总有两个交点；（2）根据题意得＝3，解得m1＝0，m2＝2，即m为0或2时，抛物线与x轴的两个交点间的距离是3．20．（6分）如图，抛物线y＝x2+bx+c经过坐标原点，并与x轴交于点A（2，0）．（1）求此抛物线的解析式；（2）写出顶点坐标及对称轴；（3）若抛物线上有一点B，且S△OAB＝3，求点B的坐标． 【分析】（1）直接把（0，0），（2，0）代入y＝x2+bx+c中，列方程组求b、c的值即可；（2）将二次函数解析式写成顶点式，可求顶点坐标及对称轴；（3）设点B的坐标为（c，d），根据三角形的面积公式求d的值，再将纵坐标d代入抛物线解析式求c的值，确定B点坐标．【解答】解：（1）把（0，0），（2，0）代入y＝x2+bx+c得，解得，…（1分）∴解析式为y＝x2﹣2x…（1分）（2）∵y＝x2﹣2x＝（x﹣1）2﹣1，∴顶点为（1，﹣1）…（1分）对称轴为：直线x＝1…（1分）（3）设点B的坐标为（c，d），则×2|d|＝3，解得d＝3或d＝﹣3，∵顶点纵坐标为﹣1，﹣3＜﹣1（或x2﹣2x＝﹣3中，x无解）∴d＝3…（1分）∴x2﹣2x＝3解得x1＝3，x2＝﹣1∴点B的坐标为（3，3）或（﹣1，3）…（1分）四、解答题（二）（本大题3小题，每小题7分，共21分） 21．（7分）如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，坐标分别为A（2，2），B（1，0），C（3，1）．（1）画出△ABC关于y轴对称的△A1B1C1；（2）画出将△ABC绕原点O顺时针旋转90°所得的△A2B2C2；（3）△A1B1C1与△A2B2C2成中心对称图形吗？若成中心对称图形，直接写出对称中心的坐标．【分析】（1）利用利用y轴对称的点的坐标特征写出A1、B1、C1的坐标，然后描点即可；（2）利用网格特点和旋转的性质画出A2、B2、C2，从而得到△A2B2C2；（3）根据中心对称的定义进行判断．【解答】解：（1）如图，△A1B1C1为所作；（2）如图，△A2B2C2为所作；（3）△A1B1C1与△A2B2C2成中心对称图形，对称中心的坐标为（﹣，﹣）． 22．（7分）如图，在⊙O中，点C、D在优弧上，将弧沿BC折叠后，点D的对应点E刚好落在弦AB上，连接AC、EC．（1）证明：AC＝EC；（2）连接AD，若CE＝5，AD＝8，求⊙O的半径．【分析】（1）先由折叠的性质得：，BC垂直平分DE，再由圆周角定理得∠CBD＝∠CBE，则，得，即可得出结论；（2）解连接OC交AD于H，连接OA，设⊙O的半径为r，由（1）得：，AC＝CE＝5，则OC⊥AD，由垂径定理得AH＝AD＝4，再由勾股定理求出CH＝3，则OH＝OC﹣CH＝r﹣3，然后在Rt△AOH中，由勾股定理得出方程，解方程即可．【解答】（1）证明：由折叠的性质得：，BC垂直平分DE，∴∠CBD＝∠CBE， ∴，∴，∴AC＝EC；（2）解：连接OC交AD于H，连接OA，如图所示：设⊙O的半径为r，由（1）得：，AC＝CE＝5，∴OC⊥AD，∴AH＝AD＝4，∠AHC＝∠AHO＝90°，∴CH＝＝＝3，∴OH＝OC﹣CH＝r﹣3，在Rt△AOH中，由勾股定理得：42+（r﹣3）2＝r2，解得：r＝，即⊙O的半径为．23．（7分）如图，是400米跑道示意图，中间的足球场ABCD是矩形，两边是半圆，直道AB的长是多少？你一定知道是100米!可你也许不知道，这不仅仅为了比赛的需要，还有另外一个原因，等你做完本题就明白了．设AB＝x米． （1）请用含x的代数式表示BC．（2）设矩形ABCD的面积为S．①求出S关于x的函数表达式．②当直道AB为多少米时，矩形ABCD的面积最大？【分析】（1）由半圆的长度两种计算方法，列出方程可求解；（2）①由矩形的面积公式可求解；②由二次函数的性质可求解．【解答】解：（1）由题意可得：π•BC＝，∴BC＝；（2）①∵四边形ABCD是矩形，∴S＝×x＝﹣（x﹣100）2+；②当x＝100时，S最大，∴当AB＝100米时，S最大．五、解答题（三）（本大题2小题，每小题10分，共20分）24．（10分）如图，点E是正方形ABCD的边BC上一点，连接DE，将DE绕着点E逆时针旋转90°，得到EG，过点G作GF⊥CB，垂足为F，GH⊥AB，垂足为H，连接DG，交AB于I．（1）求证：四边形BFGH是正方形；（2）求证：ED平分∠CEI； （3）连接IE，若正方形ABCD的边长为3，则△BEI的周长为　6　．【分析】（1）首先证明四边形FBHG是矩形，再证明FB＝FG即可解决问题．（2）延长BC到J，使得CJ＝AI．证明△IDE≌△JDE（SAS）即可解决问题．（3）证明△BIE的周长＝2AB即可解决问题．【解答】（1）证明：∵四边形ABCD是正方形，∴BC＝CD，∠DCE＝∠ABC＝∠ABF＝90°，∵GF⊥CF，GH⊥AB，∴∠F＝∠GHB＝∠FBH＝90°，∴四边形FBHG是矩形，∵ED＝EG，∠DEG＝90°，∵∠DEC+∠FEG＝90°，∠DEC+∠EDC＝90°，∴∠FEG＝∠EDC，∵∠F＝∠DCE＝90°，∴△DCE≌△EFG（AAS），∴FG＝EC，EF＝CD，∵CB＝CD，∴EF＝BC，∴BF＝EC， ∴BF＝GF，∴四边形FBHG是正方形．（2）证明：延长BC到J，使得CJ＝AI．∵DA＝DC，∠A＝∠DCJ＝90°，AI＝CJ，∴△DAI≌△DCJ（SAS），∴DI＝DJ，∠ADI＝∠CDJ，∴∠IDJ＝∠ADC＝90°，∵∠IDE＝45°，∴∠EDI＝∠EDJ＝45°，∵DE＝DE，∴△IDE≌△JDE（SAS），∴∠DEI＝∠DEJ，∴DE平分∠IEC．（3）解：∵△IDE≌△JDE，∴IE＝EJ，∵EJ＝EC+CJ，AI＝CJ，∴IE＝EC+AI，∴△BIE的周长＝BI+BE+IE＝BI+AI+BE+EC＝2AB＝6．故答案为6． 25．（10分）如图，抛物线L：y＝ax2+bx+c与x轴交于A、B（3，0）两点（A在B的左侧），与y轴交于点C（0，3），已知对称轴x＝1．（1）求抛物线L的解析式；（2）将抛物线L向下平移h个单位长度，使平移后所得抛物线的顶点落在△OBC内（包括△OBC的边界），求h的取值范围；（3）设点P是抛物线L上任一点，点Q在直线l：x＝﹣3上，△PBQ能否成为以点P为直角顶点的等腰直角三角形？若能，求出符合条件的点P的坐标；若不能，请说明理由．【分析】（1）利用待定系数法求出抛物线的解析式即可；（2）先求出直线BC解析式为y＝﹣x+3，再求出抛物线顶点坐标，得出当x＝1时，y＝2；结合抛物线顶点坐即可得出结果；（3）设P（m，﹣m2+2m+3），Q（﹣3，n），由勾股定理得出PB2＝（m﹣3）2+（﹣m2+2m+3）2，PQ2＝（m+3）2+（﹣m2+2m+3﹣n）2，BQ2＝n2+36，过P点作PM垂直于y轴，交y轴与M点，过B点作BN垂直于MP的延长线于N点，由AAS证明△PQM≌△BPN，得出MQ＝NP，PM＝BN，则MQ＝﹣m2+2m+3﹣n，PN＝3﹣m，得出方程﹣m2+2m+3﹣n＝3﹣m，解方程即可． 【解答】解：（1）∵抛物线的对称轴x＝1，B（3，0），∴A（﹣1，0）∵抛物线y＝ax2+bx+c过点C（0，3）∴当x＝0时，c＝3．又∵抛物线y＝ax2+bx+c过点A（﹣1，0），B（3，0）∴，∴∴抛物线的解析式为：y＝﹣x2+2x+3；（2）∵C（0，3），B（3，0），∴直线BC解析式为y＝﹣x+3，∵y＝﹣x2+2x+3＝﹣（x﹣1）2+4，∴顶点坐标为（1，4）对于直线BC：y＝﹣x+3，当x＝1时，y＝2，将抛物线L向下平移h个单位长度，∴当h＝2时，抛物线顶点落在BC上；当h＝4时，抛物线顶点落在OB上，∴将抛物线L向下平移h个单位长度，使平移后所得抛物线的顶点落在△OBC内（包括△OBC的边界），则2≤h≤4；（3）设P（m，﹣m2+2m+3），Q（﹣3，n），①当P点在x轴上方时，过P点作PM垂直于y轴，交y轴与M点，过B点作BN垂直于MP的延长线于N点，如图所示： ∵B（3，0），∵△PBQ是以点P为直角顶点的等腰直角三角形，∴∠BPQ＝90°，BP＝PQ，则∠PMQ＝∠BNP＝90°，∠MPQ＝∠NBP，在△PQM和△BPN中，，∴△PQM≌△BPN（AAS），∴PM＝BN，∵PM＝BN＝﹣m2+2m+3，根据B点坐标可得PN＝3﹣m，且PM+PN＝6，∴﹣m2+2m+3+3﹣m＝6，解得：m＝1或m＝0，∴P（1，4）或P（0，3）．②当P点在x轴下方时，过P点作PM垂直于l于M点，过B点作BN垂直于MP的延长线于N点，同理可得△PQM≌△BPN，∴PM＝BN，∴PM＝6﹣（3﹣m）＝3+m，BN＝m2﹣2m﹣3，则3+m＝m2﹣2m﹣3，解得m＝或．∴P（，）或（，）．综上可得，符合条件的点P的坐标是（1，4），（0，3），（，）和（，）．