人教版九年级上册数学同步课件-第24章-24直线和圆的位置关系 21页

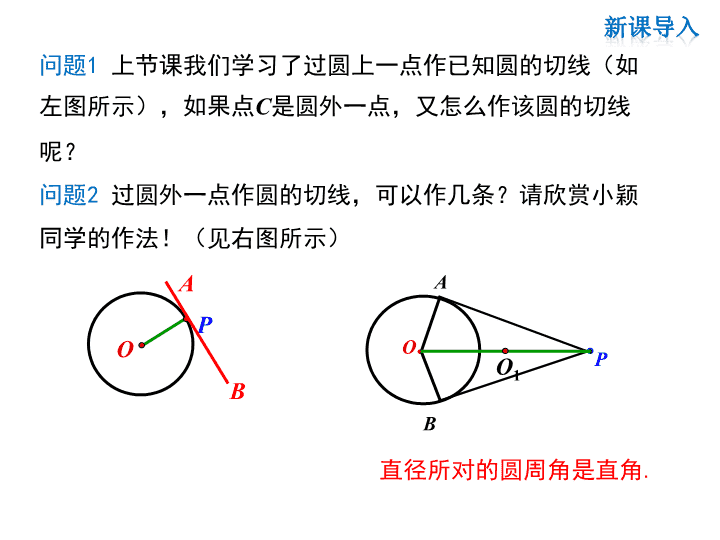
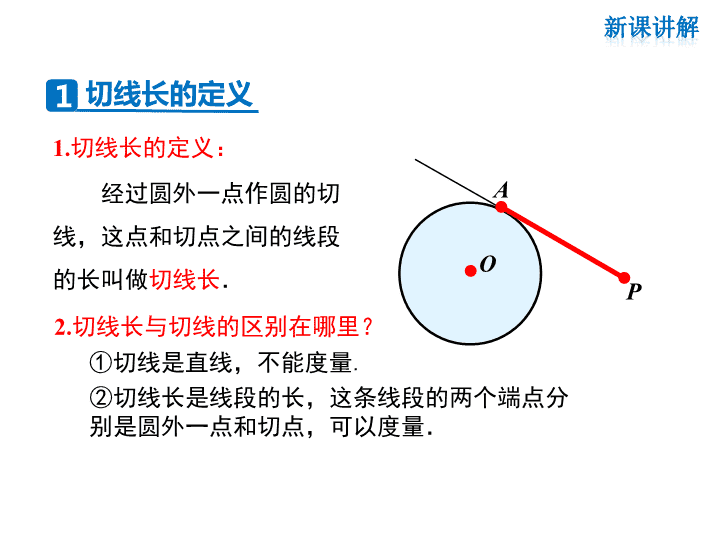
24.2直线和圆的位置关系第3课时切线长定理第二十四章圆 POO.PBAABO1问题1上节课我们学习了过圆上一点作已知圆的切线（如左图所示），如果点C是圆外一点，又怎么作该圆的切线呢？问题2过圆外一点作圆的切线，可以作几条？请欣赏小颖同学的作法！（见右图所示）直径所对的圆周角是直角.新课导入 P1.切线长的定义：经过圆外一点作圆的切线，这点和切点之间的线段的长叫做切线长．AO①切线是直线，不能度量.②切线长是线段的长，这条线段的两个端点分别是圆外一点和切点，可以度量．2.切线长与切线的区别在哪里？切线长的定义新课讲解1 思考：PA为⊙O的一条切线，沿着直线PO对折，设圆上与点A重合的点为B．OB是⊙O的一条半径吗？PB是⊙O的切线吗？（利用图形轴对称性解释）PA、PB有何关系？∠APO和∠BPO有何关系？O.PAB切线长定理新课讲解2 BPOA切线长定理:从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角.PA、PB分别切⊙O于A、BPA=PB∠OPA=∠OPB几何语言:注意：切线长定理为证明线段相等、角相等提供了新的方法.新课讲解 拓展结论PA、PB是⊙O的两条切线，A、B为切点，直线OP交⊙O于点D、E，交AB于C.（1）写出图中所有的垂直关系；OA⊥PA，OB⊥PB，AB⊥OP.（3）写出图中所有的全等三角形；△AOP≌△BOP，△AOC≌△BOC，△ACP≌△BCP.（4）写出图中所有的等腰三角形.△ABP△AOB（2）写出图中与∠OAC相等的角；∠OAC=∠OBC=∠APC=∠BPC.BPOACED新课讲解 BPOA练一练PA、PB是⊙O的两条切线，A,B是切点，OA=3.（1）若AP=4,则OP=;（2）若∠BPA=60°,则OP=.56新课讲解 ★切线长问题辅助线添加方法（3）连接圆心和圆外一点.（2）连接两切点；（1）分别连接圆心和切点；要点归纳 问题1一张三角形的铁皮，如何在它上面截下一块圆形的用料，使截出的圆与三角形各边都相切呢？ABCABC三角形的内切圆及内心新课讲解3 问题2如何作圆，使它和已知三角形的各边都相切？已知：△ABC.求作：和△ABC的各边都相切的圆.MND作法：1.作∠B和∠C的平分线BM和CN，交点为O.2.过点O作OD⊥BC,垂足为D.3.以O为圆心，OD为半径作圆O.⊙O就是所求的圆.新课讲解 1.与三角形各边都相切的圆叫做三角形的内切圆.B2.三角形内切圆的圆心叫做三角形的内心.3.这个三角形叫做圆的外切三角形.4.三角形的内心就是三角形的三个内角角平分线的交点.┐ACI┐┐DEF三角形的内心到三角形的三边的距离相等.⊙O是△ABC的内切圆，点O是△ABC的内心，△ABC是⊙O的外切三角形.概念学习新课讲解 名称确定方法图形性质外心：三角形外接圆的圆心内心：三角形内切圆的圆心三角形三边中垂线的交点1.OA=OB=OC2.外心不一定在三角形的内部．三角形三条角平分线的交点1.到三边的距离相等；2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB3.内心在三角形内部．填一填：ABOABCOC新课讲解 如图，PA、PB是⊙O的两条切线，点A、B是切点，在弧AB上任取一点C，过点C作⊙O的切线，分别交PA、PB于点D、E.已知PA=7，∠P=40°.则⑵∠DOE=.⑴△PDE的周长是；14OPABCED70°新课讲解例1 △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F，且AB=13cm，BC=14cm，CA=9cm，求AF、BD、CE的长.解:设AF=xcm，则AE=xcm.∴CE=CD=AC-AE=9-x(cm)，BF=BD=AB-AF=13-x(cm).由BD+CD=BC，可得(13-x)+(9-x)=14，解得x=4.∴AF=4cm，BD=9cm，CE=5cm.想一想：图中你能找出哪些相等的线段？理由是什么？方法小结：关键是熟练运用切线长定理，将相等线段转化集中到某条边上，从而建立方程.ACBEDFO新课讲解例2 ·ABCEDFO如图，Rt△ABC中，∠C＝90°,BC＝a,AC＝b,AB＝c,⊙O为Rt△ABC的内切圆.求Rt△ABC的内切圆的半径r.设AD=x,BE=y,CE＝r,∵⊙O与Rt△ABC的三边都相切,∴AD＝AF,BE＝BF,CE＝CD,则有x＋r＝b,y＋r＝a,x＋y＝c,解：设Rt△ABC的内切圆与三边相切于D、E、F，连结OD、OE、OF,则OA⊥AC，OE⊥BC，OF⊥AB.解得r＝a＋b－c2变式题：新课讲解. 设Rt△ABC的直角边为a、b，斜边为c，则Rt△ABC的内切圆的半径r＝a＋b－c2总结归纳新课讲解. 20°4110°A1.如图，PA、PB是⊙O的两条切线，切点分别是A、B，如果AP=4,∠APB=40°,则∠APO=,PB=.BPOA第1题2.如图，已知点O是△ABC的内心，且∠ABC=60°,∠ACB=80°,则∠BOC=.BCO第2题随堂练习 3.如图，PA、PB是⊙O的两条切线，切点为A、B,∠P=50°，点C是⊙O上异于A、B的点，则∠ACB=.65°或115°BPOA第3题4.△ABC的内切圆⊙O与三边分别切于D、E、F三点，如图，已知AF=3,BD+CE=12,则△ABC的周长是.ABCFEDO第4题30随堂练习 直角三角形的两直角边分别是3cm,4cm,试问：（1）它的外接圆半径是cm;内切圆半径是cm.·ABCEDFO2.51解：如图，△ABC的外接圆直径为AB,而由勾股定理可得AB=5cm,故外接圆半径为2.5cm.连接AO,BO,CO.设△ABC的内接圆半径为r，由面积公式可得：S△ABC=S△AOB+S△AOC+S△BOC,即，所以，代入数据得r=1cm.方法小结：直角三角形的外接圆半径等于斜边长的一半，内接圆半径.拓展提升 （2）若移动点O的位置，使⊙O保持与△ABC的边AC、BC都相切，求⊙O的半径r的取值范围.·ABODC解：如图所示，设与BC、AC相切的最大圆与BC、AC的切点分别为B、D,连接OB、OD,则四边形BODC为正方形.∴OB＝BC＝3，∴半径r的取值范围为0＜r≤3.随堂练习 切线长切线长定理作用图形的轴对称性原理提供了证线段和角相等的新方法辅助线分别连接圆心和切点；连接两切点；连接圆心和圆外一点.三角形内切圆运用切线长定理，将相等线段转化集中到某条边上，从而建立方程.有关概念内心概念及性质应用重要结论只适合于直角三角形课堂总结