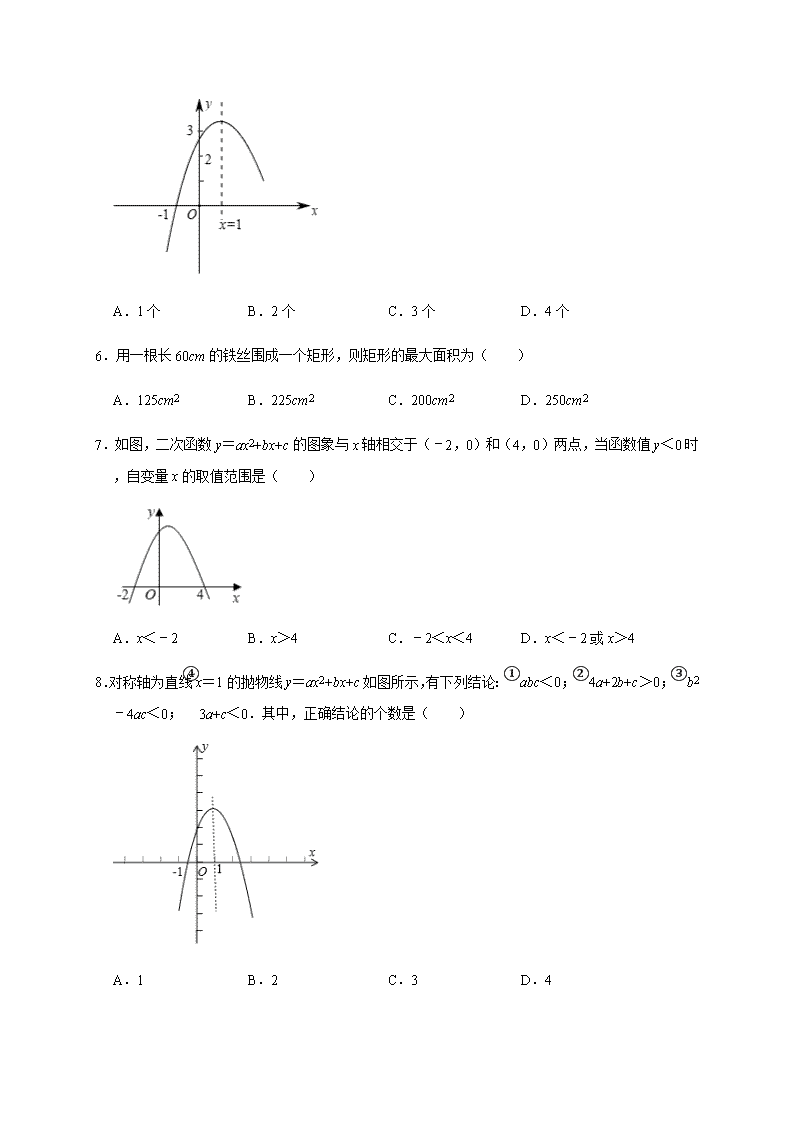人教版数学九年级上册第22章 二次函数 期末复习专项提升 6页

【二次函数】期末复习专项提升一．选择题1．将抛物线y＝x2﹣2x﹣3沿x轴折得到的新抛物线的解析式为（　　）A．y＝﹣x2+2x+3B．y＝﹣x2﹣2x﹣3C．y＝x2+2x﹣3D．y＝x2﹣2x+32．已知点A（﹣2，a），B（2，b），C（4，c）是抛物线y＝x2﹣4x上的三点，则a，b，c的大小关系为（　　）A．b＞c＞aB．b＞a＞cC．c＞a＞bD．a＞c＞b3．函数y＝ax2﹣a与y＝ax﹣a（a≠0）在同一坐标系中的图象可能是（　　）A．B．C．D．4．已知点E（2，1）在二次函数y＝x2﹣8x+m（m为常数）的图象上，则点E关于图象对称轴的对称点坐标是（　　）A．（4，1）B．（5，1）C．（6，1）D．（7，1）5．如图，二次函数y＝ax2+bx+c的图象与x轴交于点（﹣1，0），对称轴为直线x＝1，2＜c＜3，下列结论：①abc＞0；②9a+3b+c＝0；③若点，点是此函数图象上的两点，则y1＝y2；④﹣1＜a＜﹣．其中正确的个数（　　） A．1个B．2个C．3个D．4个6．用一根长60cm的铁丝围成一个矩形，则矩形的最大面积为（　　）A．125cm2B．225cm2C．200cm2D．250cm27．如图，二次函数y＝ax2+bx+c的图象与x轴相交于（﹣2，0）和（4，0）两点，当函数值y＜0时，自变量x的取值范围是（　　）A．x＜﹣2B．x＞4C．﹣2＜x＜4D．x＜﹣2或x＞48．对称轴为直线x＝1的抛物线y＝ax2+bx+c如图所示，有下列结论：①abc＜0；②4a+2b+c＞0；③b2﹣4ac＜0；④3a+c＜0．其中，正确结论的个数是（　　）A．1B．2C．3D．4 9．对于二次函数y＝x2+bx+c（b，c是常数）中自变量x与函数y的部分对应值如下表：x…﹣101234…y…1052125…下列结论正确的是（　　）A．函数图象开口向下B．当x＝5时，y＝10C．当x＞0时，y随x的增大而增大D．方程x2+bx+c＝0有两个不相等的实数根10．现有6张正面分别标有数字﹣1，0，1，2，3，4的不透明卡片，它们除数字不同外其余全部相同．现将它们背面朝上，洗匀后从中任取一张，将该卡片上的数字记为a，则使得关于x的一元二次函数y＝x2﹣2x+a﹣2与x轴有交点，且关于x的分式方程有解的所有a的和为（　　）A．2B．0C．4D．3二．填空题11．二次函数y＝（x﹣4）2﹣5的最小值是　　．12．如图，二次函数y＝﹣（x﹣2）2+k与x轴交于A，B两点，点A（﹣1，0）在B左侧，则B点坐标是　　． 13．已知二次函数y＝x2﹣2（m﹣1）x+2m2﹣m﹣2（m为常数），若对于一切实数m和x均有y≥k，则k的最大值为　　．14．竖直上抛物体时，物休离地而的高度h（m）与运动时间t（s）之间的关系可以近似地用公式h＝﹣5t2+v0t+h0表示，其中h0（m）是物体抛出时离地面的高度，v0（m/s）是物体抛出时的速度．某人将一个小球从距地面1.5m的高处以20m/s的速度竖直向上抛出，小球达到的离地面的最大高度为　　m．15．如图，抛物线y＝﹣x2+x+3与x轴交于点A，B（点A在点B的左边），交y轴于点C，点P为抛物线对称轴上一点．则△APC的周长最小值是　　．三．解答题16．已知抛物线y＝ax2﹣2ax﹣3+2a2（a≠0）．（1）求这条抛物线的对称轴；（2）若该抛物线的顶点在x轴上，求其解析式；（3）设点P（m，y1），Q（3，y2）在抛物线上，若y1＜y2，求m的取值范围．17．如图，抛物线y＝﹣x2+2x+c与x轴正半轴，y轴正半轴分别交于点A，B，且OA＝OB，点G为抛物线的顶点． （1）求抛物线的解析式及点G的坐标；（2）点M，N为抛物线上两点（点M在点N的左侧），且到对称轴的距离分别为3个单位长度和5个单位长度，点Q为抛物线上点M，N之间（含点M，N）的一个动点，求点Q的纵坐标yQ的取值范围．18．进价为每件40元的商品，售价为每件60元时，每星期可卖出300件，如果售价不低于每件45元，每件商品的售价每降1元，每星期可多卖出20件，如果售价低于45元，若再降价，则每降价1元每星期多卖出150件，设每件商品降价x元（x为正整数），每星期的销售量为y件．（1）求y与x的函数关系式并直接写出自变量x的取值范围；（2）设每星期的销售利润为w．请直接写出w与x的函数关系式；（3）每件商品的售价为多少元时，每星期可获得最大利润？每星期最大利润是多少元？ 19．某超市销售一款“免洗洗手液”，这款“免洗洗手液”的成本价为每瓶16元，当销售单价定为20元时，每天可售出80瓶．根据市场行情，现决定降价销售．市场调查反映：销售单价每降低0.5元，则每天可多售出20瓶（销售单价不低于成本价），若设这款“免洗洗手液”的销售单价为x（元），每天的销售量为y（瓶）．（1）求每天的销售量y（瓶）与销售单价x（元）之间的函数关系式；（2）当销售单价为多少元时，销售这款“免洗洗手液”每天的销售利润最大，最大利润为多少元？20．若关于x的一元二次方程ax2+bx+c＝0（a≠0）有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“2倍根方程”（1）判断一元二次方程x2﹣6x+8＝0是否是“2倍根方程”，请你说明理由；（2）若x2﹣（2m+2）x+m2+2m＝0是“2倍根方程”，求m的值．（3）若方程ax2﹣3ax+c＝0（a≠0）是2倍根方程，抛物线y＝ax2﹣3ax+c与直线y＝ax﹣2有且只有一个交点，求该点坐标．