鲁教版（五四制）2020—2021学年度第一学期九年级数学全册综合测试（三） 8页

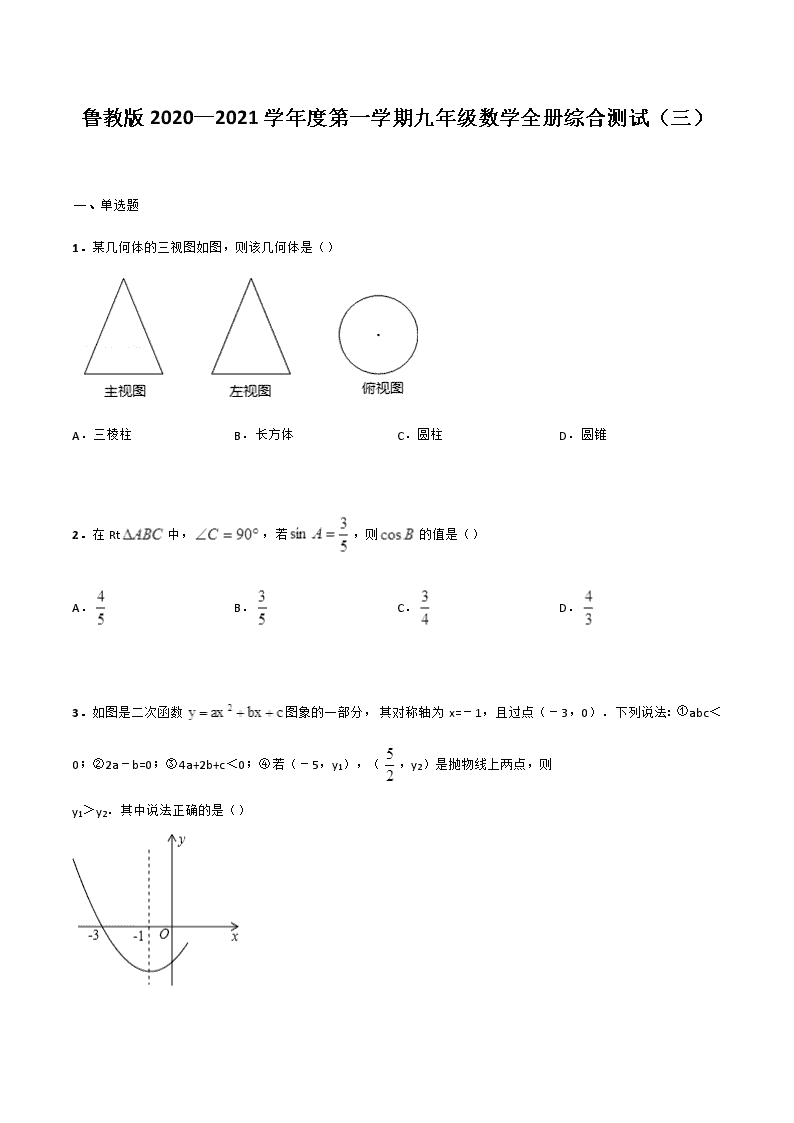
鲁教版2020—2021学年度第一学期九年级数学全册综合测试（三）一、单选题1．某几何体的三视图如图，则该几何体是（）A．三棱柱B．长方体C．圆柱D．圆锥2．在Rt中，，若，则的值是（）A．B．C．D．3．如图是二次函数图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）．下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（，y2）是抛物线上两点，则y1＞y2．其中说法正确的是（） A．①②B．②③C．①②④D．②③④4．不透明的袋子中装有两个小球，上面分别写着“1”，“2”，除数字外两个小球无其他差别．从中随机摸出一个小球，记录其数字，放回并摇匀，再从中随机摸出一个小球，记录其数字，那么两次记录的数字之和为3的概率是（   ）A．B．C．D．5．如图，边长为２的正方形ABCD的顶点A在ｙ轴上，顶点D在反比例函数y＝（x>0）的图像上，已知点B的坐标是（，），则k的值为（）A．10B．8C．6D．46．下列各点中，在函数y=－的图象上的是A．（3，1）B．（－3，1）C．（，3）D．（3，－） 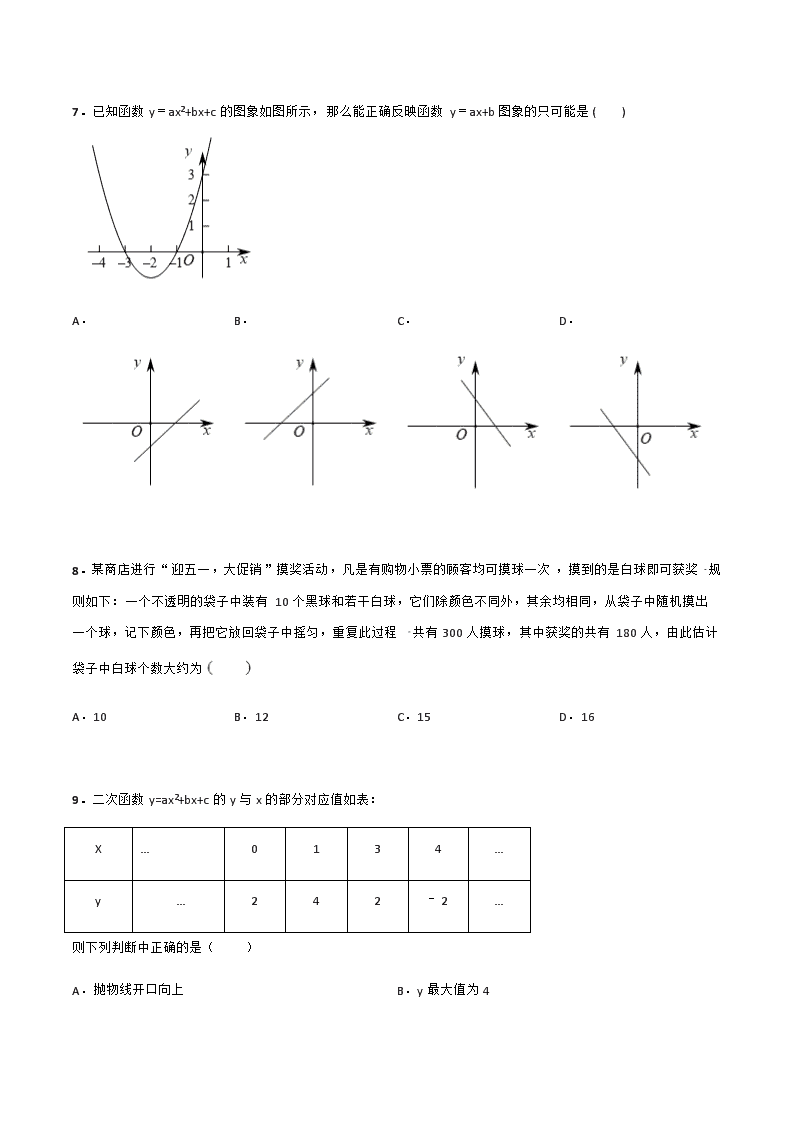7．已知函数y＝ax2+bx+c的图象如图所示，那么能正确反映函数y＝ax+b图象的只可能是(　　)A．B．C．D．8．某商店进行“迎五一，大促销”摸奖活动，凡是有购物小票的顾客均可摸球一次，摸到的是白球即可获奖规则如下：一个不透明的袋子中装有10个黑球和若干白球，它们除颜色不同外，其余均相同，从袋子中随机摸出一个球，记下颜色，再把它放回袋子中摇匀，重复此过程共有300人摸球，其中获奖的共有180人，由此估计袋子中白球个数大约为　　A．10B．12C．15D．169．二次函数y=ax2+bx+c的y与x的部分对应值如表：X…0134…y …242﹣2…则下列判断中正确的是（　　）A．抛物线开口向上B．y最大值为4 C．当x＞1时，y随著x的增大而减小D．当0＜x＜2时，y＞210．口袋中有若干个形状大小完全相同的白球，为估计袋中白球的个数，现往口袋中放入10个形状大小与白球相同的红球．混匀后从口袋中随机摸出40个球，发现其中有3个红球．设袋中有白球x个，则可用于估计袋中白球个数的方程是（   ）A．B．C．D．11．如图为△ABC的内切圆，点D，E分别为边AB，AC上的点，且DE为⊙I的切线，若△ABC的周长为21，BC边的长为6，则△ADE的周长为（　　）A．15B．9C．7.5D．712．准备两组相同的牌，每组两张且大小相同，两张牌的牌面数字分别是0，1，从每组牌中各摸出一张牌，两张牌的牌面数字和为1的概率为（  ）A．B．C．D．二、填空题 13．如图，中，，，将绕点顺时针旋转得到，当，，三点共线时，旋转角为，连接，交于于点，下面结论：①为等腰三角形；②；③；④；⑤中，正确的结论有___________个．14．已知直线y＝kx＋2与y轴交于点A，与双曲线y＝相交于B，C两点，若AB＝3AC，则k的值为______．15．在Rt△ABC中，∠C=90°，a=2，b=3，则cosA= ．16．⊙M的圆心在一次函数y=x+2图象上，半径为1．当⊙M与y轴相切时，点M的坐标为_____． 17．如图，在平行四边形中，，，，点在线段上一动点，连接，将沿着翻折，得，连接、．则面积的最小值为______．三、解答题18．如图，海岛A四周30海里范围内是暗礁区，一艘货轮由东向西航行，在B处见岛A在北偏西60º，航行20海里后到C处，见岛A在北偏西45º，货轮继续向西航行，有无触礁危险？19．抛物线y＝－x2＋5x＋n经过点A（1，0），与x轴交于点C，与y轴交于点B，顶点为D.（1）求n的值和D点坐标；（2）求四边形ABCD的面积.20．已知反比例函数的图象经过点．写出函数表达式；这个函数的图象在哪几个象限？随的增大怎样变化？ 点、在这个函数的图象上吗？如果点在图象上，求的值．21．如图，直线交轴于点，交轴于点，抛物线经过点和点，与轴的另一个交点为点.点在直线上方的抛物线上运动，且点的横坐标为，过作轴交直线于，作轴于，交直线于点.（1）求抛物线所对应的函数表达式；（2）若的长为，求关于的函数关系式；（3）在点的运动过程中，当时，试求出的值与的值.22．计算：2cos245°－－(sin60°－1)0＋()－2.23．如图，给出了几个小立方块所塔几何体从上面看到的形状，小正方形中的数字表示该位置的小立方块的个数.请你画出这个几何体从正面和左面看到的形状图. 24．如图，直线l1：与双曲线相交于点A（a，2），将直线l1向上平移3个单位得到l2，直线l2与双曲线相交于B．C两点（点B在第一象限），交y轴于D点．（1）求双曲线的解析式；（2）求tan∠DOB的值．