2020九年级数学上册 第一次质量评估试卷 （新版）浙教版 7页

上册·第一次质量评估试卷 ‎[考查范围：第1章]‎ 一、选择题(每小题3分，共30分)‎ ‎1．若y＝(－m)xm2－3是二次函数，且开口向上，则m的值为(　B　)‎ A．±　　　　　　 B．－　　　　　 C.　　　　　　　D．0‎ ‎2．抛物线y＝ax2＋bx－3经过点(2，4)，则代数式‎8a＋4b＋1的值为(　C　)‎ A．3 B．‎9 ‎ C．15 D．－15 ‎ 第3题图 ‎3．已知抛物线y＝ax2＋bx＋c的图象如图所示，则点P(ab，b＋c)所在的象限为(　D　)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎4．二次函数y＝ax2－4x＋1有最小值－3，则a的值为(　A　)‎ A．1 B．－‎1 ‎ C．±1 D. 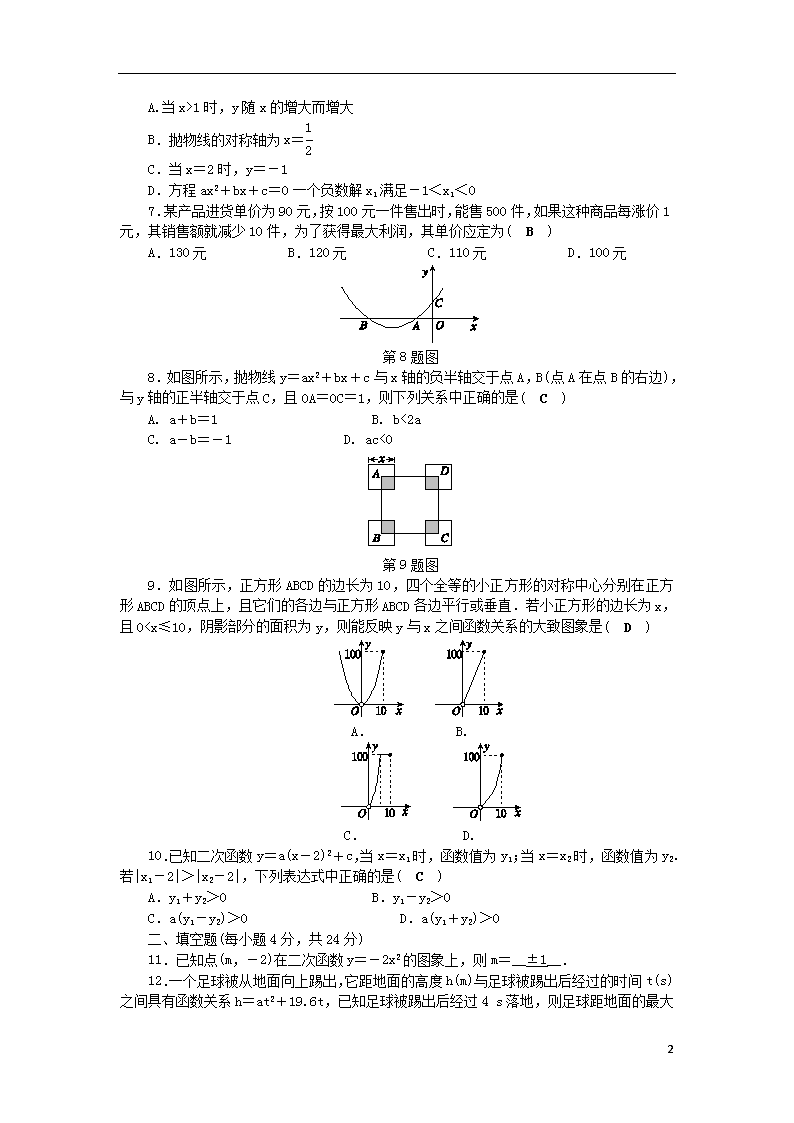‎5．一抛物线的形状、开口方向与y＝x2－4x＋3相同，顶点为(－2，1)．此抛物线的解析式为(　C　)‎ A．y＝(x－2)2＋1 B．y＝(x＋2)2－1‎ C．y＝(x＋2)2＋1 D．y＝－(x＋2)2＋1‎ ‎6．抛物线y＝ax2＋bx＋c上部分点的横坐标x、纵坐标y的对应值如下表，则下列说法中错误的是(　A　)‎ x ‎…‎ ‎－3‎ ‎－2‎ ‎－1‎ ‎0‎ ‎1‎ ‎…‎ y ‎…‎ ‎－21‎ ‎－9‎ ‎－1‎ ‎3‎ ‎3‎ ‎…‎ 7‎ A.当x>1时，y随x的增大而增大　　　　 ‎ B．抛物线的对称轴为x＝ C．当x＝2时，y＝－1　　　　　　　　　　　　　‎ D．方程ax2＋bx＋c＝0一个负数解x1满足－1＜x1＜0‎ ‎7．某产品进货单价为90元，按100元一件售出时，能售500件，如果这种商品每涨价1元，其销售额就减少10件，为了获得最大利润，其单价应定为(　B　)‎ A．130元 B．120元 C．110元 D．100元 第8题图 ‎8．如图所示，抛物线y＝ax2＋bx＋c与x轴的负半轴交于点A，B(点A在点B的右边)，与y轴的正半轴交于点C，且OA＝OC＝1，则下列关系中正确的是(　C　)‎ A. a＋b＝1 B. b<‎‎2a C. a－b＝－1 D. ac<0‎ 第9题图 ‎9．如图所示，正方形ABCD的边长为10，四个全等的小正方形的对称中心分别在正方形ABCD的顶点上，且它们的各边与正方形ABCD各边平行或垂直．若小正方形的边长为x，且00，且Δ＝12－‎4a(1－a)＝1－‎4a＋‎4a2＝(1－‎2a)2>0.‎ ‎∴a>0，且a≠.‎ ‎20．(8分)某高中学校为高一新生设计的单人桌的抽屉部分是长方体．其中，抽屉底面周长为‎180 cm，高为‎20 cm.请通过计算说明，当底面的宽x为何值时，抽屉的体积y最大？最大为多少？(材质及其厚度等忽略不计)‎ 解：已知抽屉底面宽为x cm，则底面长为180÷2－x＝(90－x)cm.‎ ‎∵90－x≥x，∴0＜x≤45，‎ 由题意，得y＝x(90－x)×20＝－20(x2－90x)＝－20(x－45)2＋40500‎ ‎∵0＜x≤45，－20＜0，‎ ‎∴当x＝45时，y有最大值，最大值为40500.‎ 答：当抽屉底面宽为45 cm时，抽屉的体积最大，最大体积为40500 cm3.‎ 第21题图 ‎21．(8分)如图是一种新型娱乐设施的示意图，x轴所在位置记为地面，平台AB∥x轴，OA＝‎6米，AB＝‎2米，BC是反比例函数y＝的图象的一部分，CD是二次函数y＝－x2＋mx＋n图象的一部分，连结点C为抛物线的顶点，且C点到地面的距离为‎2米，D点是娱乐设施与地面的一个接触点．‎ ‎(1)试求k，m，n的值；‎ ‎(2)试求点B与点D的水平距离．‎ 解：(1)把B(2，6)代入y＝，可得y＝，把y＝2代入y＝，可得x＝6，即C点坐标为(6，2)．‎ ‎∵二次函数y＝－x2＋mx＋n的顶点为C，∴y＝－(x－6)2＋2，∴y＝－x2＋12x－34.‎ ‎∴k＝12，m＝12，n＝－34.‎ ‎(2)把y＝0代入y＝－(x－6)2＋2，解得x1＝6＋，x2＝6－.‎ 故点B与点D的水平距离为6＋－2＝4＋(米)．‎ ‎22．(8分)某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于40%.经试销发现，销售量y(件)与销售单价x(元)符合一次函数y＝kx＋b，且当x＝80时，y＝40；当x＝70时，y＝50.‎ 7‎ ‎(1)求一次函数y＝kx＋b的表达式；‎ ‎(2)若该商场获得的利润为W元，试写出利润W与销售单价x之间的关系式；销售单价定为多少元时，商场可获得最大利润？最大利润是多少元？‎ 解：(1)60≤x≤60(1＋40%)，∴60≤x≤84，‎ 由题意，得解之得 ‎∴一次函数的解析式为y＝－x＋120(60≤x≤84)．‎ ‎(2)销售额为xy＝x(－x＋120)元；成本：60y＝60(－x＋120)．‎ ‎∴W＝xy－60y，‎ ‎＝x(－x＋120)－60(－x＋120)，‎ ‎＝(x－60)(－x＋120)，‎ ‎＝－x2＋180x－7200，‎ ‎＝－(x－90)2＋900，‎ ‎∴W＝－(x－90)2＋900(60≤x≤84)，‎ 当x＝84时，W取得最大值，最大值是－(84－90)2＋900＝864(元)．‎ 即销售单价定为每件84元时，可获得最大利润，最大利润是864元．‎ 第23题图 ‎23．(10分)如图所示，抛物线经过A(－1，0)，B(5，0)，C三点．‎ ‎(1)求抛物线的解析式；‎ ‎(2)在抛物线的对称轴上有一点P，使PA＋PC的值最小，求点P的坐标；‎ ‎(3)点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．‎ 解：(1)设抛物线的解析式为y＝ax2＋bx＋c(a≠0)，‎ ‎∵A(－1，0)，B(5，0)，C三点在抛物线上，‎ ‎∴解得 ‎∴抛物线的解析式为y＝x2－2x－.‎ ‎(2)∵抛物线的解析式为y＝x2－2x－.‎ 7‎ ‎∴其对称轴为直线x＝－＝－＝2，连结BC，‎ ‎∵B(5，0)，C，∴设直线BC的解析式为y＝kx＋b(k≠0)，‎ ‎∴解得 ‎∴直线BC的解析式为y＝x－，‎ 当x＝2时，y＝1－＝－，∴P.‎ ‎(3)存在．符合条件的点N的坐标为或或.‎ 第24题图 ‎24．(12分)如图所示，在平面直角坐标系中，抛物线y＝－x2＋2x＋3与x轴的交点为A，B(点A在点B的左侧)，与y轴的交点为C，连结BC.点M是抛物线上A，C之间的一个动点，过点M作MN∥BC，分别交x轴、抛物线于D，N，过点M作EF⊥x轴，垂足为F，并交直线BC于点E，‎ ‎(1)求点A，B，C的坐标；‎ ‎(2)当点M恰好是EF的中点，求BD的长；‎ ‎(3)连结DE，记△DEM，△BDE的面积分别为S1，S2，当BD＝1时，请求S2－S1的值．‎ 解：(1)A(－1，0)，B(3，0)，C(0，3)．‎ ‎(2)∵ B(3，0)，C(0，3)，‎ ‎∴BC的函数解析式为y＝－x＋3.‎ 设M(m，－m2＋2m＋3)，则E(m，－m＋3)．‎ ‎∵M为EF中点，‎ ‎∴－m2＋2m＋3＝，解得m1＝3，m2＝－.‎ ‎∵M在A，C两点之间，∴m＝－.‎ 则M的坐标为.‎ 7‎ 又∵MD∥BC，‎ ‎∴MD的函数解析式为y＝－x＋，故D∴BD＝.‎ ‎(3)由图形可知，D在B点左侧，当BD＝1时，D点坐标为(2，0)，‎ ‎∴此时MD的函数解析式为y＝－x＋2.‎ 则解得x1＝，x2＝(舍去)．‎ ‎∴M点的坐标为，‎ 则E为，‎ ‎∴ME＝1，DF＝，EF＝.‎ ‎∴S2－S1＝×1×－×1×＝.‎ 7‎