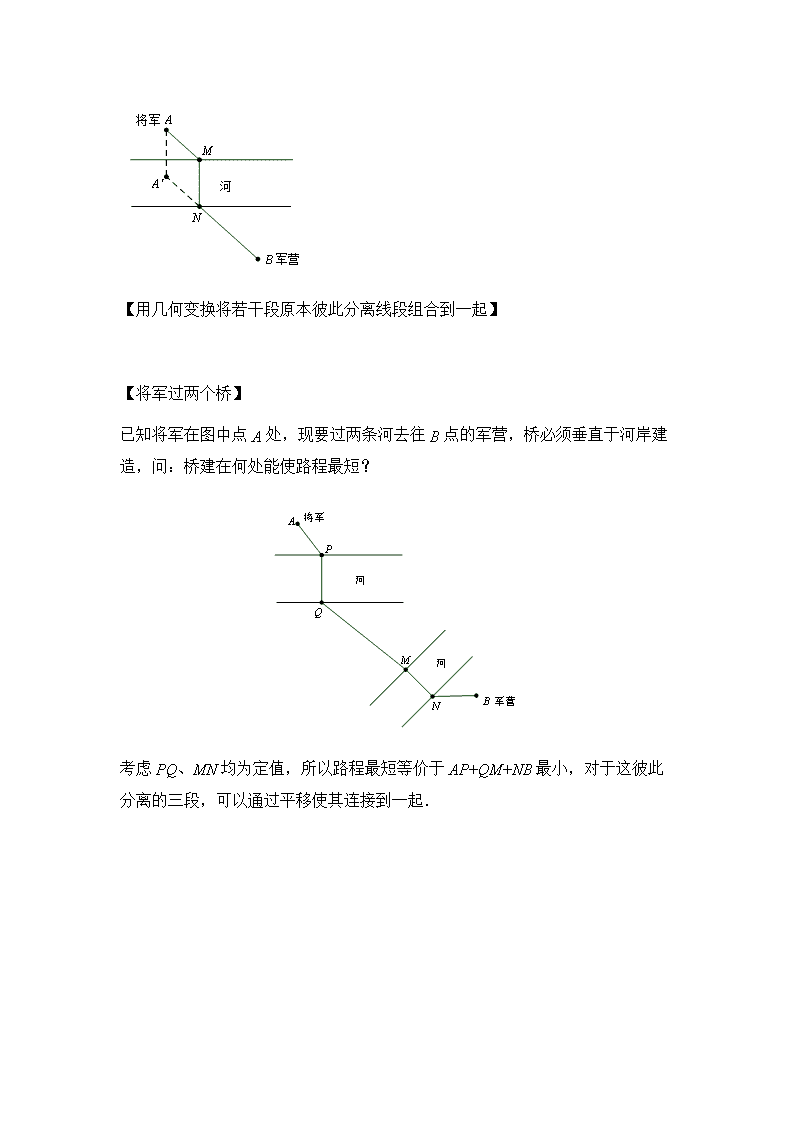2021中考数学复习微专题 “将军过桥问题”突破与提升策略 6页

中考数学复习微专题：“将军过桥问题”突破与提升策略 【将军过桥】 已知将军在图中点 A 处，现要过河去往 B 点的军营，桥必须垂直于河岸建造， 问：桥建在何处能使路程最短？ 考虑 MN 长度恒定，只要求 AM+NB 最小值即可．问题在于 AM、NB 彼此分离， 所以首先通过平移，使 AM 与 NB 连在一起，将 AM 向下平移使得 M、N 重合， 此时 A 点落在 A’位置． 问题化为求 A’N+NB 最小值，显然，当共线时，值最小，并得出桥应建的位置． 【用几何变换将若干段原本彼此分离线段组合到一起】 【将军过两个桥】 已知将军在图中点 A 处，现要过两条河去往 B 点的军营，桥必须垂直于河岸建 造，问：桥建在何处能使路程最短？ 考虑 PQ、MN 均为定值，所以路程最短等价于 AP+QM+NB 最小，对于这彼此分 离的三段，可以通过平移使其连接到一起． AP 平移至 A’Q，NB 平移至 MB’，化 AP+QM+NB 为 A’Q+QM+MB’． 当 A’、Q、M、B’共线时，A’Q+QM+MB’取到最小值，再依次确定 P、N 位置． 【将军遛马】 如图，将军在 A 点处，现在将军要带马去河边喝水，并沿着河岸走一段路，再 返回军营，问怎么走路程最短？ 【问题简化】已知 A、B 两点，MN 长度为定值，求确定 M、N 位置使得 AM+MN+NB 值最小？ 【分析】考虑 MN 为定值，故只要 AM+BN 值最小即可．将 AM 平移使 M、N 重 合，AM=A’N，将 AM+BN 转化为 A’N+NB． 构造点 A 关于 MN 的对称点 A’’，连接 A’’B，可依次确定 N、M 位置，可得路线． 【例题】如图，在平面直角坐标系中，矩形 ABCD 的顶点 B 在原点，点 A、C 在 坐标轴上，点 D 的坐标为（6，4），E 为 CD 的中点，点 P、Q 为 BC 边上两个动 点，且 PQ=2，要使四边形 APQE 的周长最小，则点 P 的坐示应为______________． 【分析】考虑 PQ、AE 为定值，故只要 AP+QE 最小即可，如图，将 AP 平移至 A’Q，考虑 A’Q+QE 最小值． 作点 A’关于 x 轴的对称点 A’’，连接 A’’E，与 x 轴交点即为 Q 点，左移 2 个单位 即得 P 点． 【练习】如图，矩形 ABCD 中，AD=2，AB=4，AC 为对角线，E、F 分别为边 AB、CD 上的动点，且 EF⊥AC 于点 M，连接 AF、CE，求 AF+CE 的最小值． 【分析】此题难点在于要得到 AF 与 CE 之间的关系，方能将这两条线段联系到 一起．过点 E 作 EH⊥CD 交 CD 于 H 点，由相似可得：FH=1． 连接 BH，则 BH=CE 问题转化为 BH+AF 最小值． 参考将军遛马的作法，作出图形，得出 AF+BH=A’H+B’H=A’B’=5．