2019年四川省达州市中考数学试卷含答案 32页

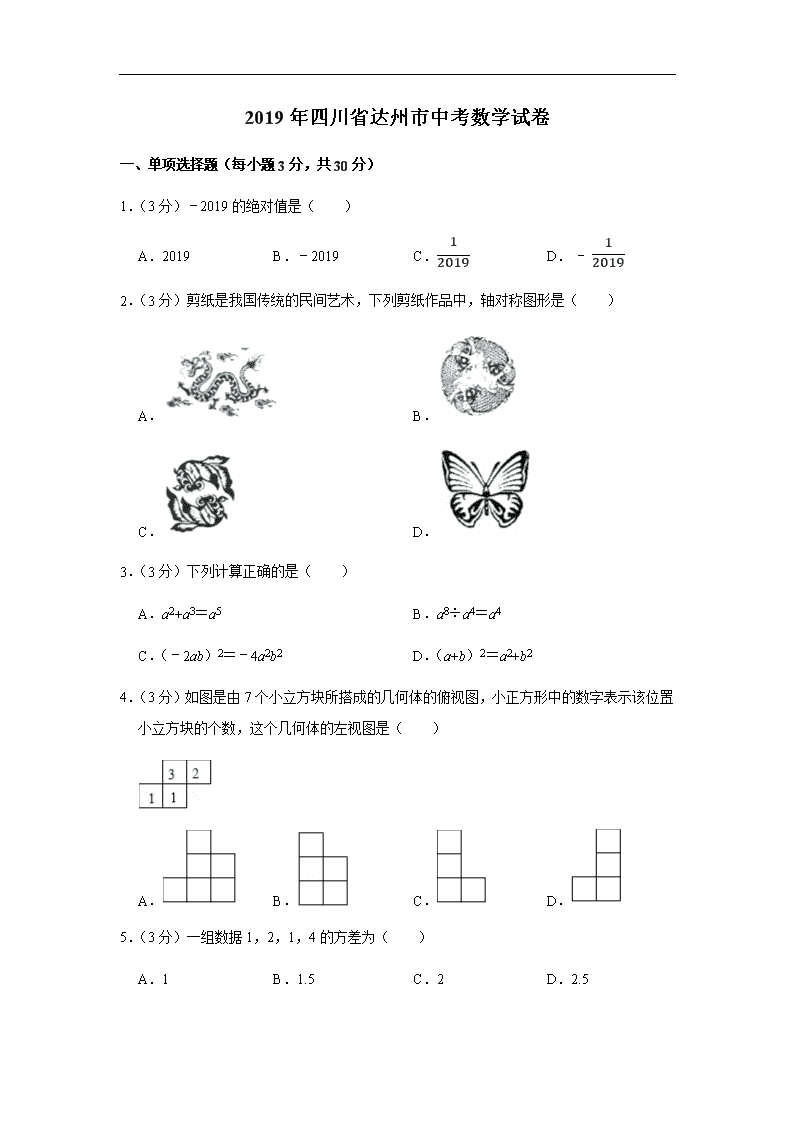
‎2019年四川省达州市中考数学试卷 一、单项选择题（每小题3分，共30分）‎ ‎1．（3分）﹣2019的绝对值是（　　）‎ A．2019 B．﹣2019 C．‎1‎‎2019‎ D．‎‎-‎‎1‎‎2019‎ ‎2．（3分）剪纸是我国传统的民间艺术，下列剪纸作品中，轴对称图形是（　　）‎ A． B． ‎ C． D．‎ ‎3．（3分）下列计算正确的是（　　）‎ A．a2+a3＝a5 B．a8÷a4＝a4 ‎ C．（﹣2ab）2＝﹣4a2b2 D．（a+b）2＝a2+b2‎ ‎4．（3分）如图是由7个小立方块所搭成的几何体的俯视图，小正方形中的数字表示该位置小立方块的个数，这个几何体的左视图是（　　）‎ A． B． C． D．‎ ‎5．（3分）一组数据1，2，1，4的方差为（　　）‎ A．1 B．1.5 C．2 D．2.5‎ ‎6．（3分）下列判断正确的是（　　）‎ A．‎5‎‎-1‎‎2‎‎＜‎0.5 ‎ B．若ab＝0，则a＝b＝0 ‎ C．ab‎=‎ab ‎ D．3a可以表示边长为a的等边三角形的周长 ‎7．（3分）某公司今年4月的营业额为2500万元，按计划第二季度的总营业额要达到9100万元，设该公司5、6两月的营业额的月平均增长率为x．根据题意列方程，则下列方程正确的是（　　）‎ A．2500（1+x）2＝9100 ‎ B．2500（1+x%）2＝9100 ‎ C．2500（1+x）+2500（1+x）2＝9100 ‎ D．2500+2500（1+x）+2500（1+x）2＝9100‎ ‎8．（3分）a是不为1的有理数，我们把‎1‎‎1-a称为a的差倒数，如2的差倒数为‎1‎‎1-2‎‎=-‎1，﹣1的差倒数‎1‎‎1-(-1)‎‎=‎‎1‎‎2‎，已知a1＝5，a2是a1的差倒数，a3是a2的差倒数，a4是a3的差倒数…，依此类推，a2019的值是（　　）‎ A．5 B．‎-‎‎1‎‎4‎ C．‎4‎‎3‎ D．‎‎4‎‎5‎ ‎9．（3分）如图，边长都为4的正方形ABCD和正三角形EFG如图放置，AB与EF在一条直线上，点A与点F重合．现将△EFG沿AB方向以每秒1个单位的速度匀速运动，当点F与B重合时停止．在这个运动过程中，正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图象大致是（　　）‎ A． B． C． D．‎ ‎10．（3分）矩形OABC在平面直角坐标系中的位置如图所示，已知B（2‎3‎，2），点A在x轴上，点C在y轴上，P是对角线OB上一动点（不与原点重合），连接PC，过点P作PD⊥PC，交x轴于点D．下列结论：‎ ‎①OA＝BC＝2‎3‎；‎ ‎②当点D运动到OA的中点处时，PC2+PD2＝7；‎ ‎③在运动过程中，∠CDP是一个定值；‎ ‎④当△ODP为等腰三角形时，点D的坐标为（‎2‎‎3‎‎3‎，0）．‎ 其中正确结论的个数是（　　）‎ A．1个 B．2个 C．3个 D．4个 二、填空题（每小题3分，共18分）‎ ‎11．（3分）2018年，中国贸易进出口总额为4.62万亿美元（美国约为4.278万亿美元），同比增长12.6%，占全球贸易总额的11.75%，贸易总额连续两年全球第一！数据4.62万亿用科学记数法表示为　 　．‎ ‎12．（3分）如图所示的电路中，当随机闭合开关S1、S2、S3中的两个时，能够让灯泡发光的概率为　 　．‎ ‎13．（3分）如图所示，点C位于点A、B之间（不与A、B重合），点C表示1﹣2x，则x的取值范围是　 　．‎ ‎14．（3分）如图，▱ABCD的对角线AC、BD相交于点O，点E是AB的中点，△BEO的周长是8，则△BCD的周长为　 　．‎ ‎15．（3分）如图，A、B两点在反比例函数y‎=‎k‎1‎x的图象上，C、D两点在反比例函数y‎=‎k‎2‎x的图象上，AC⊥x轴于点E，BD⊥x轴于点F，AC＝2，BD＝4，EF＝3，则k2﹣k1＝　 　．‎ ‎16．（3分）如图，抛物线y＝﹣x2+2x+m+1（m为常数）交y轴于点A，与x轴的一个交点在2和3之间，顶点为B．‎ ‎①抛物线y＝﹣x2+2x+m+1与直线y＝m+2有且只有一个交点；‎ ‎②若点M（﹣2，y1）、点N（‎1‎‎2‎，y2）、点P（2，y3）在该函数图象上，则y1＜y2＜y3；‎ ‎③将该抛物线向左平移2个单位，再向下平移2个单位，所得抛物线解析式为y＝﹣（x+1）2+m；‎ ‎④点A关于直线x＝1的对称点为C，点D、E分别在x轴和y轴上，当m＝1时，四边形BCDE周长的最小值为‎34‎‎+‎‎2‎．‎ 其中正确判断的序号是　 　．‎ 三、解答题：解答时应写出必要的文字说明、证明过程或演算步骤（共72分）‎ ‎17．（5分）计算：（π﹣3.14）0﹣（‎1‎‎2‎）﹣2‎+‎3‎‎27‎-‎‎8‎．‎ ‎18．（7分）先化简：（x-2‎x‎2‎‎+2x‎-‎x-1‎x‎2‎‎+4x+4‎）‎÷‎‎4-xx，再选取一个适当的x的值代入求值．‎ ‎19．（7分）随机抽取某小吃店一周的营业额（单位：元）如下表：‎ 星期一 星期二 星期三 星期四 星期五 星期六 星期日 合计 ‎540‎ ‎680‎ ‎640‎ ‎640‎ ‎780‎ ‎1110‎ ‎1070‎ ‎5460‎ ‎（1）分析数据，填空：这组数据的平均数是　 　元，中位数是　 　元，众数是　 　元．‎ ‎（2）估计一个月的营业额（按30天计算）：‎ ‎①星期一到星期五营业额相差不大，用这5天的平均数估算合适么？‎ 答（填“合适”或“不合适”）：　 　．‎ ‎②选择一个你认为最合适的数据估算这个小吃店一个月的营业额．‎ ‎20．（7分）如图，在Rt△ABC中，∠ACB＝90°，AC＝2，BC＝3．‎ ‎（1）尺规作图：不写作法，保留作图痕迹．‎ ‎①作∠ACB的平分线，交斜边AB于点D；‎ ‎②过点D作BC的垂线，垂足为点E．‎ ‎（2）在（1）作出的图形中，求DE的长．‎ ‎21．（7分）端午节前后，张阿姨两次到超市购买同一种粽子．节前，按标价购买，用了96元；节后，按标价的6折购买，用了72元，两次一共购买了27个．这种粽子的标价是多少？‎ ‎22．（8分）如图，⊙O是△ABC的外接圆，∠BAC的平分线交⊙O于点D，交BC于点E，过点D作直线DF∥BC．‎ ‎（1）判断直线DF与⊙O的位置关系，并说明理由；‎ ‎（2）若AB＝6，AE‎=‎‎12‎‎3‎‎5‎，CE‎=‎‎4‎‎7‎‎5‎，求BD的长．‎ ‎23．（8分）渠县賨人谷是国家AAAA级旅游景区，以“奇山奇水奇石景，古賨古洞古部落”享誉巴渠，被誉为川东“小九寨”．端坐在观音崖旁的一块奇石似一只“啸天犬”，昂首向天，望穿古今．一个周末，某数学兴趣小组的几名同学想测出“啸天犬”上嘴尖与头顶的距离．他们把蹲着的“啸天犬”抽象成四边形ABCD，想法测出了尾部C看头顶B的仰角为40°，从前脚落地点D看上嘴尖A的仰角刚好60°，CB＝5m，CD＝2.7m ‎．景区管理员告诉同学们，上嘴尖到地面的距离是3m．于是，他们很快就算出了AB的长．你也算算？（结果精确到0.1m．参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84.‎2‎‎≈‎1.41，‎3‎‎≈‎1.73）‎ ‎24．（11分）箭头四角形 模型规律 如图1，延长CO交AB于点D，则∠BOC＝∠1+∠B＝∠A+∠C+∠B．‎ 因为凹四边形ABOC形似箭头，其四角具有“∠BOC＝∠A+∠B+∠C”这个规律，所以我们把这个模型叫做“箭头四角形”．‎ 模型应用 ‎（1）直接应用：①如图2，∠A+∠B+∠C+∠D+∠E+∠F＝　 　．‎ ‎②如图3，∠ABE、∠ACE的2等分线（即角平分线）BF、CF交于点F，已知∠BEC＝120°，∠BAC＝50°，则∠BFC＝　 　．‎ ‎③如图4，BOi、COi分别为∠ABO、∠ACO的2019等分线（i＝1，2，3，…，2017，2018）．它们的交点从上到下依次为O1、O2、O3、…、O2018．已知∠BOC＝m°，∠BAC＝n°，则∠BO1000C＝　 　度．‎ ‎（2）拓展应用：如图5，在四边形ABCD中，BC＝CD，∠BCD＝2∠BAD．O是四边形ABCD内一点，且OA＝OB＝OD．求证：四边形OBCD是菱形．‎ ‎25．（12分）如图1，已知抛物线y＝﹣x2+bx+c过点A（1，0），B（﹣3，0）．‎ ‎（1）求抛物线的解析式及其顶点C的坐标；‎ ‎（2）设点D是x轴上一点，当tan（∠CAO+∠CDO）＝4时，求点D的坐标；‎ ‎（3）如图2．抛物线与y轴交于点E，点P是该抛物线上位于第二象限的点，线段PA交BE于点M，交y轴于点N，△BMP和△EMN的面积分别为m、n，求m﹣n的最大值．‎ ‎2019年四川省达州市中考数学试卷 参考答案与试题解析 一、单项选择题（每小题3分，共30分）‎ ‎1．（3分）﹣2019的绝对值是（　　）‎ A．2019 B．﹣2019 C．‎1‎‎2019‎ D．‎‎-‎‎1‎‎2019‎ ‎【解答】解：﹣2019的绝对值是：2019．‎ 故选：A．‎ ‎2．（3分）剪纸是我国传统的民间艺术，下列剪纸作品中，轴对称图形是（　　）‎ A． B． ‎ C． D．‎ ‎【解答】解：A、不是轴对称图形，故此选项不合题意；‎ B、不是轴对称图形，故此选项不合题意；‎ C、不是轴对称图形，故此选项不合题意；‎ D、是轴对称图形，故此选项符合题意；‎ 故选：D．‎ ‎3．（3分）下列计算正确的是（　　）‎ A．a2+a3＝a5 B．a8÷a4＝a4 ‎ C．（﹣2ab）2＝﹣4a2b2 D．（a+b）2＝a2+b2‎ ‎【解答】解：A、a2+a3，无法计算，故此选项错误；‎ B、a8÷a4＝a4，故此选项正确；‎ C、（﹣2ab）2＝4a2b2，故此选项错误；‎ D、（a+b）2＝a2+2ab+b2，故此选项错误；‎ 故选：B．‎ ‎4．（3分）如图是由7个小立方块所搭成的几何体的俯视图，小正方形中的数字表示该位置小立方块的个数，这个几何体的左视图是（　　）‎ A． B． C． D．‎ ‎【解答】解：从左面看可得到从左到右分别是3，1个正方形．‎ 故选：C．‎ ‎5．（3分）一组数据1，2，1，4的方差为（　　）‎ A．1 B．1.5 C．2 D．2.5‎ ‎【解答】解：‎ 平均数为x‎=‎1+2+1+4‎‎4‎=‎2‎ 方差S2‎=‎‎1‎‎4‎[（1﹣2）2+（2﹣2）2+（1﹣2）2+（4﹣2）2]‎‎=‎‎3‎‎2‎ 故选：B．‎ ‎6．（3分）下列判断正确的是（　　）‎ A．‎5‎‎-1‎‎2‎‎＜‎0.5 ‎ B．若ab＝0，则a＝b＝0 ‎ C．ab‎=‎ab ‎ D．3a可以表示边长为a的等边三角形的周长 ‎【解答】解：A、2‎＜‎5‎＜‎3，‎ ‎∴‎1‎‎2‎‎＜‎5‎‎-1‎‎2‎＜‎1，本选项错误；‎ B、若ab＝0，则a＝0或b＝0或a＝b＝0，本选项错误；‎ C、当a≥0，b＞0时，ab‎=‎ab成立，本选项错误；‎ D、3a可以表示边长为a的等边三角形的周长，本选项正确；‎ 故选：D．‎ ‎7．（3分）某公司今年4月的营业额为2500万元，按计划第二季度的总营业额要达到9100万元，设该公司5、6两月的营业额的月平均增长率为x．根据题意列方程，则下列方程正确的是（　　）‎ A．2500（1+x）2＝9100 ‎ B．2500（1+x%）2＝9100 ‎ C．2500（1+x）+2500（1+x）2＝9100 ‎ D．2500+2500（1+x）+2500（1+x）2＝9100‎ ‎【解答】解：设该公司5、6两月的营业额的月平均增长率为x．根据题意列方程得：‎ ‎2500+2500（1+x）+2500（1+x）2＝9100．‎ 故选：D．‎ ‎8．（3分）a是不为1的有理数，我们把‎1‎‎1-a称为a的差倒数，如2的差倒数为‎1‎‎1-2‎‎=-‎1，﹣1的差倒数‎1‎‎1-(-1)‎‎=‎‎1‎‎2‎，已知a1＝5，a2是a1的差倒数，a3是a2的差倒数，a4是a3的差倒数…，依此类推，a2019的值是（　　）‎ A．5 B．‎-‎‎1‎‎4‎ C．‎4‎‎3‎ D．‎‎4‎‎5‎ ‎【解答】解：∵a1＝5，‎ a2‎=‎1‎‎1-‎a‎1‎=‎1‎‎1-5‎=-‎‎1‎‎4‎，‎ a3‎=‎1‎‎1-‎a‎2‎=‎1‎‎1-(-‎1‎‎4‎)‎=‎‎4‎‎5‎，‎ a4‎=‎1‎‎1-‎a‎3‎=‎1‎‎1-‎‎4‎‎5‎=‎5，‎ ‎…‎ ‎∴数列以5，‎-‎‎1‎‎4‎，‎4‎‎5‎三个数依次不断循环，‎ ‎∵2019÷3＝673，‎ ‎∴a2019＝a3‎=‎‎4‎‎5‎，‎ 故选：D．‎ ‎9．（3分）如图，边长都为4的正方形ABCD和正三角形EFG如图放置，AB与EF在一条直线上，点A与点F重合．现将△EFG沿AB方向以每秒1个单位的速度匀速运动，当点F与B重合时停止．在这个运动过程中，正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图象大致是（　　）‎ A． B． C． D．‎ ‎【解答】解：当0≤t≤2时，S‎=t⋅(t⋅tan60°)‎‎2‎=‎‎3‎‎2‎t‎2‎，即S与t是二次函数关系，有最小值（0，0），开口向上，‎ 当2＜t≤4时，S‎=‎4×(4×sin60°)‎‎2‎-‎(4-t)⋅[(4-t)⋅tan60°]‎‎2‎=4‎3‎-‎3‎‎2‎(4-t‎)‎‎2‎，即S与t是二次函数关系，开口向下，‎ 由上可得，选项C符合题意，‎ 故选：C．‎ ‎10．（3分）矩形OABC在平面直角坐标系中的位置如图所示，已知B（2‎3‎，2），点A在x轴上，点C在y轴上，P是对角线OB上一动点（不与原点重合），连接PC，过点P作PD⊥PC，交x轴于点D．下列结论：‎ ‎①OA＝BC＝2‎3‎；‎ ‎②当点D运动到OA的中点处时，PC2+PD2＝7；‎ ‎③在运动过程中，∠CDP是一个定值；‎ ‎④当△ODP为等腰三角形时，点D的坐标为（‎2‎‎3‎‎3‎，0）．‎ 其中正确结论的个数是（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎【解答】解：①∵四边形OABC是矩形，B（2‎3‎，2），‎ ‎∴OA＝BC＝2‎3‎；故①正确；‎ ‎②∵点D为OA的中点，‎ ‎∴OD‎=‎‎1‎‎2‎OA‎=‎‎3‎，‎ ‎∴PC2+PD2＝CD2＝OC2+OD2＝22+（‎3‎）2＝7，故②正确；‎ ‎③如图，过点P作PF⊥OA于F，FP的延长线交BC于E，‎ ‎∴PE⊥BC，四边形OFEC是矩形，‎ ‎∴EF＝OC＝2，‎ 设PE＝a，则PF＝EF﹣PE＝2﹣a，‎ 在Rt△BEP中，tan∠CBO‎=PEBE=OCBC=‎‎3‎‎3‎，‎ ‎∴BE‎=‎‎3‎PE‎=‎‎3‎a，‎ ‎∴CE＝BC﹣BE＝2‎3‎‎-‎‎3‎a‎=‎‎3‎（2﹣a），‎ ‎∵PD⊥PC，‎ ‎∴∠CPE+∠FPD＝90°，‎ ‎∵∠CPE+∠PCE＝90°，‎ ‎∴∠FPD＝∠ECP，‎ ‎∵∠CEP＝∠PFD＝90°，‎ ‎∴△CEP∽△PFD，‎ ‎∴PEFD‎=‎CPPD，‎ ‎∴aFD‎=‎‎3‎‎(2-a)‎‎2-a，‎ ‎∴FD‎=‎a‎3‎，‎ ‎∴tan∠PDC‎=PCPD=aa‎3‎=‎‎3‎，‎ ‎∴∠PDC＝60°，故③正确；‎ ‎④∵B（2‎3‎，2），四边形OABC是矩形，‎ ‎∴OA＝2‎3‎，AB＝2，‎ ‎∵tan∠AOB‎=ABOA=‎‎3‎‎3‎，‎ ‎∴∠AOB＝30°，‎ 当△ODP为等腰三角形时，‎ Ⅰ、OD＝PD，‎ ‎∴∠DOP＝∠DPO＝30°，‎ ‎∴∠ODP＝60°，‎ ‎∴∠ODC＝60°，‎ ‎∴OD‎=‎‎3‎‎3‎OC‎=‎‎2‎‎3‎‎3‎，‎ Ⅱ、OP＝OD，‎ ‎∴∠ODP＝∠OPD＝75°，‎ ‎∵∠COD＝∠CPD＝90°，‎ ‎∴∠OCP＝105°＞90°，故不合题意舍去；‎ Ⅲ、OP＝PD，‎ ‎∴∠POD＝∠PDO＝30°，‎ ‎∴∠OCP＝150°＞90°故不合题意舍去，‎ ‎∴当△ODP为等腰三角形时，点D的坐标为（‎2‎‎3‎‎3‎，0）．故④正确，‎ 故选：D．‎ 二、填空题（每小题3分，共18分）‎ ‎11．（3分）2018年，中国贸易进出口总额为4.62万亿美元（美国约为4.278万亿美元），同比增长12.6%，占全球贸易总额的11.75%，贸易总额连续两年全球第一！数据4.62万亿用科学记数法表示为　4.62×1012　．‎ ‎【解答】解：4.62万亿＝4.62×1012，‎ 故答案为：4.62×1012‎ ‎12．（3分）如图所示的电路中，当随机闭合开关S1、S2、S3中的两个时，能够让灯泡发光的概率为　‎2‎‎3‎　．‎ ‎【解答】解：因为随机闭合开关S1，S2，S3中的两个，有3种方法，其中有2种能够让灯泡发光 所以P（灯泡发光）‎=‎‎2‎‎3‎．‎ 故本题答案为：‎2‎‎3‎．‎ ‎13．（3分）如图所示，点C位于点A、B之间（不与A、B重合），点C表示1﹣2x，则x的取值范围是　‎-‎1‎‎2‎＜‎x＜0　．‎ ‎【解答】解：根据题意得：1＜1﹣2x＜2，‎ 解得：‎-‎1‎‎2‎＜‎x＜0，‎ 则x的范围是‎-‎1‎‎2‎＜‎x＜0，‎ 故答案为：‎-‎1‎‎2‎＜‎x＜0‎ ‎14．（3分）如图，▱ABCD的对角线AC、BD相交于点O，点E是AB的中点，△BEO的周长是8，则△BCD的周长为　16　．‎ ‎【解答】解：∵▱ABCD的对角线AC、BD相交于点O，‎ ‎∴BO＝DO‎=‎‎1‎‎2‎BD，BD＝2OB，‎ ‎∴O为BD中点，‎ ‎∵点E是AB的中点，‎ ‎∴AB＝2BE，BC＝2OE，‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴AB＝CD，‎ ‎∴CD＝2BE．‎ ‎∵△BEO的周长为8，‎ ‎∴OB+OE+BE＝8，‎ ‎∴BD+BC+CD＝2OB+2OE+2BE＝2（OB+OE+BE）＝16，‎ ‎∴△BCD的周长是16，‎ 故答案为16．‎ ‎15．（3分）如图，A、B两点在反比例函数y‎=‎k‎1‎x的图象上，C、D两点在反比例函数y‎=‎k‎2‎x的图象上，AC⊥x轴于点E，BD⊥x轴于点F，AC＝2，BD＝4，EF＝3，则k2﹣k1＝　4　．‎ ‎【解答】解：设A（a，k‎1‎a），C（a，k‎2‎a），B（b，k‎1‎b），D（b，k‎2‎b），则 CA‎=k‎2‎a-k‎1‎a=‎2，‎ ‎∴k‎2‎‎-‎k‎1‎a‎=2‎，‎ 得a‎=‎k‎2‎‎-‎k‎1‎‎2‎ 同理：BD‎=k‎1‎‎-‎k‎2‎b=4‎，得b‎=‎k‎1‎‎-‎k‎2‎‎4‎ 又∵a﹣b＝3‎ ‎∴k‎2‎‎-‎k‎1‎‎2‎‎-k‎1‎‎-‎k‎2‎‎4‎=‎3‎ 解得：k2﹣k1＝4‎ ‎16．（3分）如图，抛物线y＝﹣x2+2x+m+1（m为常数）交y轴于点A，与x轴的一个交点在2和3之间，顶点为B．‎ ‎①抛物线y＝﹣x2+2x+m+1与直线y＝m+2有且只有一个交点；‎ ‎②若点M（﹣2，y1）、点N（‎1‎‎2‎，y2）、点P（2，y3）在该函数图象上，则y1＜y2＜y3；‎ ‎③将该抛物线向左平移2个单位，再向下平移2个单位，所得抛物线解析式为y＝﹣（x+1）2+m；‎ ‎④点A关于直线x＝1的对称点为C，点D、E分别在x轴和y轴上，当m ‎＝1时，四边形BCDE周长的最小值为‎34‎‎+‎‎2‎．‎ 其中正确判断的序号是　①③④　．‎ ‎【解答】解：①把y＝m+2代入y＝﹣x2+2x+m+1中，得x2﹣2x+1＝0，∵△＝4﹣4＝0，∴此方程两个相等的实数根，则抛物线y＝﹣x2+2x+m+1与直线y＝m+2有且只有一个交点，故此小题结论正确；‎ ‎②∵抛物线的对称轴为x＝1，∴点P（2，y3）关于x＝1的对称点为P′（0，y3），∵a＝﹣1＜0，∴当x＜1时，y随x增大而减小，又∵﹣2＜0‎＜‎‎1‎‎2‎，点M（﹣2，y1）、点N（‎1‎‎2‎，y2）、点P′（0，y3）在该函数图象上，∴y2＜y3＜y1，故此小题结论错误；‎ ‎③将该抛物线向左平移2个单位，再向下平移2个单位，抛物线的解析式为：y＝﹣（x+2）2+2（x+2）x+m+1﹣2，即y＝﹣（x+1）2+m，故此小题结论正确；‎ ‎④当m＝1时，抛物线的解析式为：y＝﹣x2+2x+2，∴A（0，2），C（2，2），B（1，3），作点B关于y轴的对称点B′（﹣1，3），作C点关于x轴的对称点C′（2，﹣2），连接B′C′，与x轴、y轴分别交于D、E点，如图，‎ 则BE+ED+CD+BC＝B′E+ED+C′D+BC＝B′C′+BC，根据两点之间线段最短，知B′‎ C′最短，而BC的长度一定，∴此时，四边形BCDE周长＝B′C′+BC最小，为：B'M‎2‎+C'‎M‎2‎‎+BM‎2‎+CM‎2‎=‎3‎‎2‎‎+‎‎5‎‎2‎+‎1‎‎2‎‎+‎‎1‎‎2‎=‎34‎+‎‎2‎，故此小题结论正确；‎ 故答案为：①③④．‎ 三、解答题：解答时应写出必要的文字说明、证明过程或演算步骤（共72分）‎ ‎17．（5分）计算：（π﹣3.14）0﹣（‎1‎‎2‎）﹣2‎+‎3‎‎27‎-‎‎8‎．‎ ‎【解答】解：原式＝1﹣4+3﹣2‎‎2‎ ‎＝﹣2‎2‎．‎ ‎18．（7分）先化简：（x-2‎x‎2‎‎+2x‎-‎x-1‎x‎2‎‎+4x+4‎）‎÷‎‎4-xx，再选取一个适当的x的值代入求值．‎ ‎【解答】解：‎ 化简得，‎ 原式‎=[x-2‎x(x+2)‎-x-1‎‎(x+2‎‎)‎‎2‎]÷‎‎4-xx ‎=[‎(x+2)(x-2)‎x(x+2‎‎)‎‎2‎-x(x-1)‎x(x+2‎‎)‎‎2‎]×‎x‎4-x‎ ‎ ‎=-‎‎1‎‎(x+2‎‎)‎‎2‎‎ ‎ 取x＝1得，原式‎=-‎1‎‎(1+2‎‎)‎‎2‎=-‎‎1‎‎9‎ ‎19．（7分）随机抽取某小吃店一周的营业额（单位：元）如下表：‎ 星期一 星期二 星期三 星期四 星期五 星期六 星期日 合计 ‎540‎ ‎680‎ ‎640‎ ‎640‎ ‎780‎ ‎1110‎ ‎1070‎ ‎5460‎ ‎（1）分析数据，填空：这组数据的平均数是　780　元，中位数是　680　元，众数是　640　元．‎ ‎（2）估计一个月的营业额（按30天计算）：‎ ‎①星期一到星期五营业额相差不大，用这5天的平均数估算合适么？‎ 答（填“合适”或“不合适”）：　不合适　．‎ ‎②选择一个你认为最合适的数据估算这个小吃店一个月的营业额．‎ ‎【解答】解：（1）这组数据的平均数‎=‎5460‎‎7‎=‎780（元）；‎ 按照从小到大排列为540、640、640、680、780、1070、1110，‎ 中位数为680元，众数为640元；‎ 故答案为：780，680，640；‎ ‎（2）①因为在周一至周日的营业额中周六、日的营业额明显高于其他五天的营业额，‎ 所以去掉周六、日的营业额对平均数的影响较大，‎ 故用该店本周星期一到星期五的日平均营业额估计当月的营业总额不合适；‎ 故答案为：不合适；‎ ‎②用该店本周一到周日的日均营业额估计当月营业额，‎ 当月的营业额为30×780＝23400（元）．‎ ‎20．（7分）如图，在Rt△ABC中，∠ACB＝90°，AC＝2，BC＝3．‎ ‎（1）尺规作图：不写作法，保留作图痕迹．‎ ‎①作∠ACB的平分线，交斜边AB于点D；‎ ‎②过点D作BC的垂线，垂足为点E．‎ ‎（2）在（1）作出的图形中，求DE的长．‎ ‎【解答】解：（1）如图，DE为所作；‎ ‎（2）∵CD平分∠ACB，‎ ‎∴∠BCD‎=‎‎1‎‎2‎∠ACB＝45°，‎ ‎∵DE⊥BC，‎ ‎∴△CDE为等腰直角三角形，‎ ‎∴DE＝CE，‎ ‎∵DE∥AC，‎ ‎∴△BDE∽△BAC，‎ ‎∴DEAC‎=‎BEBC，即DE‎2‎‎=‎‎3-DE‎3‎，‎ ‎∴DE‎=‎‎6‎‎5‎．‎ ‎21．（7分）端午节前后，张阿姨两次到超市购买同一种粽子．节前，按标价购买，用了96元；节后，按标价的6折购买，用了72元，两次一共购买了27个．这种粽子的标价是多少？‎ ‎【解答】解：设这种粽子的标价是x元/个，则节后的价格是0.6x元/个，‎ 依题意，得：‎96‎x‎+‎72‎‎0.6x=‎27，‎ 解得：x＝8，‎ 经检验，x＝8是原方程的解，且符合题意．‎ 答：这种粽子的标价是8元/个．‎ ‎22．（8分）如图，⊙O是△ABC的外接圆，∠BAC的平分线交⊙O于点D，交BC于点E，过点D作直线DF∥BC．‎ ‎（1）判断直线DF与⊙O的位置关系，并说明理由；‎ ‎（2）若AB＝6，AE‎=‎‎12‎‎3‎‎5‎，CE‎=‎‎4‎‎7‎‎5‎，求BD的长．‎ ‎【解答】解：（1）DF与⊙O相切，‎ 理由：连接OD，‎ ‎∵∠BAC的平分线交⊙O于点D，‎ ‎∴∠BAD＝∠CAD，‎ ‎∴BD‎=‎CD，‎ ‎∴OD⊥BC，‎ ‎∵DF∥BC，‎ ‎∴OD⊥DF，‎ ‎∴DF与⊙O相切；‎ ‎（2）∵∠BAD＝∠CAD，∠ADB＝∠C，‎ ‎∴△ABD∽△AEC，‎ ‎∴ABAE‎=‎BDCE，‎ ‎∴‎6‎‎12‎‎3‎‎5‎‎=‎BD‎4‎‎7‎‎5‎，‎ ‎∴BD‎=‎‎2‎‎21‎‎3‎．‎ ‎23．（8分）渠县賨人谷是国家AAAA级旅游景区，以“奇山奇水奇石景，古賨古洞古部落”享誉巴渠，被誉为川东“小九寨”．端坐在观音崖旁的一块奇石似一只“啸天犬”，昂首向天，望穿古今．一个周末，某数学兴趣小组的几名同学想测出“啸天犬”上嘴尖与头顶的距离．他们把蹲着的“啸天犬”抽象成四边形ABCD，想法测出了尾部C看头顶B的仰角为40°，从前脚落地点D看上嘴尖A的仰角刚好60°，CB＝5m，CD＝2.7m．景区管理员告诉同学们，上嘴尖到地面的距离是3m．于是，他们很快就算出了AB的长．你也算算？（结果精确到0.1m．参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84.‎2‎‎≈‎1.41，‎3‎‎≈‎1.73）‎ ‎【解答】解：作BF⊥CE于F，‎ 在Rt△BFC中，BF＝BC•sin∠BCF≈3.20，‎ CF＝BC•cos∠BCF≈3.85，‎ 在Rt△ADE中，DE‎=ADtan∠ADE=‎3‎‎3‎=‎3‎≈‎1.73，‎ ‎∴BH＝BF﹣HF＝0.20，AH＝EF＝CD+DE﹣CF＝0.58，‎ 由勾股定理得，AB‎=BH‎2‎+AH‎2‎≈‎0.6（m），‎ 答：AB的长约为0.6m．‎ ‎24．（11分）箭头四角形 模型规律 如图1，延长CO交AB于点D，则∠BOC＝∠1+∠B＝∠A+∠C+∠B．‎ 因为凹四边形ABOC形似箭头，其四角具有“∠BOC＝∠A+∠B+∠C”这个规律，所以我们把这个模型叫做“箭头四角形”．‎ 模型应用 ‎（1）直接应用：①如图2，∠A+∠B+∠C+∠D+∠E+∠F＝　2α　．‎ ‎②如图3，∠ABE、∠ACE的2等分线（即角平分线）BF、CF交于点F，已知∠BEC＝120°，∠BAC＝50°，则∠BFC＝　85°　．‎ ‎③如图4，BOi、COi分别为∠ABO、∠ACO的2019等分线（i＝1，2，3，…，2017，2018）．它们的交点从上到下依次为O1、O2、O3、…、O2018．已知∠BOC＝m°，∠BAC＝n°，则∠BO1000C＝　（‎1000‎‎2019‎m‎+‎‎1019‎‎2019‎n）　度．‎ ‎（2）拓展应用：如图5，在四边形ABCD中，BC＝CD，∠BCD＝2∠BAD．O是四边形ABCD内一点，且OA＝OB＝OD．求证：四边形OBCD是菱形．‎ ‎【解答】解：（1）①如图2，‎ 在凹四边形ABOC中，∠A+∠B+∠C＝∠BOC＝α，‎ 在凹四边形DOEF中，∠D+∠E+∠F＝∠DOE＝α，‎ ‎∴∠A+∠B+∠C+∠D+∠E+∠F＝2α；‎ ‎②如图3，‎ ‎∵∠BEC＝∠EBF+∠ECF+∠F，∠F＝∠ABF+∠ACF+∠A，且∠EBF＝∠ABF，∠ECF＝∠ACF，‎ ‎∴∠BEC＝∠F﹣∠A+∠F，‎ ‎∴∠F‎=‎‎∠BEC+∠A‎2‎，‎ ‎∵∠BEC＝120°，∠BAC＝50°，‎ ‎∴∠F＝85°；‎ ‎③如图3，‎ 由题意知∠ABO1000‎=‎‎1000‎‎2019‎∠ABO，∠OBO1000‎=‎‎1019‎‎2019‎∠ABO，‎ ‎∠ACO1000‎=‎‎1000‎‎2019‎∠ACO，∠OCO1000‎=‎‎1019‎‎2019‎∠ACO，‎ ‎∴∠BOC＝∠OBO1000+∠OCO1000+∠BO1000C‎=‎‎1019‎‎2019‎（∠ABO+∠ACO）+∠BO1000C，‎ ‎∠BO1000C＝∠ABO1000+∠ACO1000+∠BAC‎=‎‎1000‎‎2019‎（∠ABO+∠ACO）+∠BAC，‎ 则∠ABO+∠ACO‎=‎‎2019‎‎1000‎（∠BO1000C﹣∠BAC），‎ 代入∠BOC‎=‎‎1019‎‎2019‎（∠ABO+∠ACO）+∠BO1000C得∠BOC‎=‎1019‎‎2019‎×‎‎2019‎‎1000‎（∠BO1000C﹣∠BAC）+∠BO1000C，‎ 解得：∠BO1000C‎=‎‎1000‎‎2019‎（∠BOC‎+‎‎1019‎‎1000‎∠BAC）‎=‎‎1000‎‎2019‎∠BOC‎+‎‎1019‎‎2019‎∠BAC，‎ ‎∵∠BOC＝m°，∠BAC＝n°，‎ ‎∴∠BO1000C‎=‎‎1000‎‎2019‎m°‎+‎‎1019‎‎2019‎n°；‎ 故答案为：①2α；②85°；③（‎1000‎‎2019‎m‎+‎‎1019‎‎2019‎n）；‎ ‎（2）如图5，连接OC，‎ ‎∵OA＝OB＝OD，‎ ‎∴∠OAB＝∠OBA，∠OAD＝∠ODA，‎ ‎∴∠BOD＝∠BAD+∠ABO+∠ADO＝2∠BAD，‎ ‎∵∠BCD＝2∠BAD，‎ ‎∴∠BCD＝∠BOD，‎ ‎∵BC＝CD，OA＝OB＝OD，OC是公共边，‎ ‎∴△OBC≌△ODC（SSS），‎ ‎∴∠BOC＝∠DOC，∠BCO＝∠DCO，‎ ‎∵∠BOD＝∠BOC+∠DOC，∠BCD＝∠BCO+∠DCO，‎ ‎∴∠BOC‎=‎‎1‎‎2‎∠BOD，∠BCO‎=‎‎1‎‎2‎∠BCD，‎ 又∠BOD＝∠BCD，‎ ‎∴∠BOC＝∠BCO，‎ ‎∴BO＝BC，‎ 又OB＝OD，BC＝CD，‎ ‎∴OB＝BC＝CD＝DO，‎ ‎∴四边形OBCD是菱形．‎ ‎25．（12分）如图1，已知抛物线y＝﹣x2+bx+c过点A（1，0），B（﹣3，0）．‎ ‎（1）求抛物线的解析式及其顶点C的坐标；‎ ‎（2）设点D是x轴上一点，当tan（∠CAO+∠CDO）＝4时，求点D的坐标；‎ ‎（3）如图2．抛物线与y轴交于点E，点P是该抛物线上位于第二象限的点，线段PA交BE于点M，交y轴于点N，△BMP和△EMN的面积分别为m、n，求m﹣n的最大值．‎ ‎【解答】解：（1）由题意把点（1，0），（﹣3，0）代入y＝﹣x2+bx+c，‎ 得，‎-1+b+c=0‎‎-9-3b+c=0‎，‎ 解得b＝﹣2，c＝3，‎ ‎∴y＝﹣x2﹣2x+3‎ ‎＝﹣（x+1）2+4，‎ ‎∴此抛物线解析式为：y＝﹣x2﹣2x+3，顶点C的坐标为（﹣1，4）；‎ ‎（2）∵抛物线顶点C（﹣1，4），‎ ‎∴抛物线对称轴为直线x＝﹣1，‎ 设抛物线对称轴与x轴交于点H，‎ 则H（﹣1，0），‎ 在Rt△CHO中，CH＝4，OH＝1，‎ ‎∴tan∠COH‎=CHOH=‎4，‎ ‎∵∠COH＝∠CAO+∠ACO，‎ ‎∴当∠ACO＝∠CDO时，‎ tan（∠CAO+∠CDO）＝tan∠COH＝4，‎ 如图1，当点D在对称轴左侧时，‎ ‎∵∠ACO＝∠CDO，∠CAO＝∠CAO，‎ ‎∴△AOC∽△ACD，‎ ‎∴ACAD‎=‎AOAC，‎ ‎∵AC‎=CH‎2‎+AH‎2‎=‎2‎5‎，AO＝1，‎ ‎∴‎2‎‎5‎AD‎=‎‎1‎‎2‎‎5‎，‎ ‎∴AD＝20，‎ ‎∴OD＝19，‎ ‎∴D（﹣19，0）；‎ 当点D在对称轴右侧时，点D关于直线x＝1的对称点D'的坐标为（17，0），‎ ‎∴点D的坐标为（﹣19，0）或（17，0）；‎ ‎（3）设P（a，﹣a2﹣2a+3），‎ 将P（a，﹣a2﹣2a+3），A（1，0）代入y＝kx+b，‎ 得，ak+b=-a‎2‎-2a+3‎k+b=0‎，‎ 解得，k＝﹣a﹣3，b＝a+3，‎ ‎∴yPA＝（﹣a﹣3）x+a+3，‎ 当x＝0时，y＝a+3，‎ ‎∴N（0，a+3），‎ 如图2，‎ ‎∵S△BPM＝S△BPA﹣S四边形BMNO﹣S△AON，S△EMN＝S△EBO﹣S四边形BMNO，‎ ‎∴S△BPM﹣S△EMN ‎＝S△BPA﹣S△EBO﹣S△AON ‎=‎1‎‎2‎×‎‎4×（﹣a2﹣2a+3）‎-‎1‎‎2‎×‎3×3‎-‎1‎‎2‎×‎1×（a+3）‎ ‎＝﹣2a2‎-‎‎9‎‎2‎a ‎＝﹣2（a‎+‎‎9‎‎8‎）2‎+‎‎81‎‎32‎，‎ 由二次函数的性质知，当a‎=-‎‎9‎‎8‎时，S△BPM﹣S△EMN有最大值‎81‎‎32‎，‎ ‎∵△BMP和△EMN的面积分别为m、n，‎ ‎∴m﹣n的最大值为‎81‎‎32‎．‎ 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/6/30 9:34:09；用户：中考培优辅导；邮箱：p5193@xyh.com；学号：27411521‎