2019年江苏省苏州市中考数学试卷含答案 30页

‎2019年江苏省苏州市中考数学试卷 一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题要求的．请将选择题的答案用2B铅笔涂在答题卡相应位置上．‎ ‎1．（3分）5的相反数是（　　）‎ A．‎1‎‎5‎ B．‎-‎‎1‎‎5‎ C．5 D．﹣5‎ ‎2．（3分）有一组数据：2，2，4，5，7，这组数据的中位数为（　　）‎ A．2 B．4 C．5 D．7‎ ‎3．（3分）苏州是全国重点旅游城市，2018年实现旅游总收入约为26000000万元，数据26000000用科学记数法可表示为（　　）‎ A．0.26×108 B．2.6×108 C．26×106 D．2.6×107‎ ‎4．（3分）如图，已知直线a∥b，直线c与直线a，b分别交于点A，B．若∠1＝54°，则∠2等于（　　）‎ A．126° B．134° C．136° D．144°‎ ‎5．（3分）如图，AB为⊙O的切线，切点为A连接AO、BO，BO与⊙O交于点C，延长BO与⊙O交于点D，连接AD．若∠ABO＝36°，则∠ADC的度数为（　　）‎ A．54° B．36° C．32° D．27°‎ ‎6．（3分）小明用15元买售价相同的软面笔记本，小丽用24元买售价相同的硬面笔记本（两人的钱恰好用完），已知每本硬面笔记本比软面笔记本贵3元，且小明和小丽买到相同数量的笔记本，设软面笔记本每本售价为x元，根据题意可列出的方程为（　　）‎ A．‎15‎x‎=‎‎24‎x+3‎ B．‎15‎x‎=‎‎24‎x-3‎ C．‎15‎x+3‎‎=‎‎24‎x D．‎‎15‎x-3‎‎=‎‎24‎x ‎7．（3分）若一次函数y＝kx+b（k，b为常数，且k≠0）的图象经过点A（0，﹣1），B（1，1），则不等式kx+b＞1的解为（　　）‎ A．x＜0 B．x＞0 C．x＜1 D．x＞1‎ ‎8．（3分）如图，小亮为了测量校园里教学楼AB的高度，将测角仪CD竖直放置在与教学楼水平距离为18‎3‎m的地面上，若测角仪的高度是1.5m．测得教学楼的顶部A处的仰角为30°．则教学楼的高度是（　　）‎ A．55.5m B．54m C．19.5m D．18m ‎9．（3分）如图，菱形ABCD的对角线AC，BD交于点O，AC＝4，BD＝16，将△ABO沿点A到点C的方向平移，得到△A'B'O'．当点A'与点C重合时，点A与点B'之间的距离为（　　）‎ A．6 B．8 C．10 D．12‎ ‎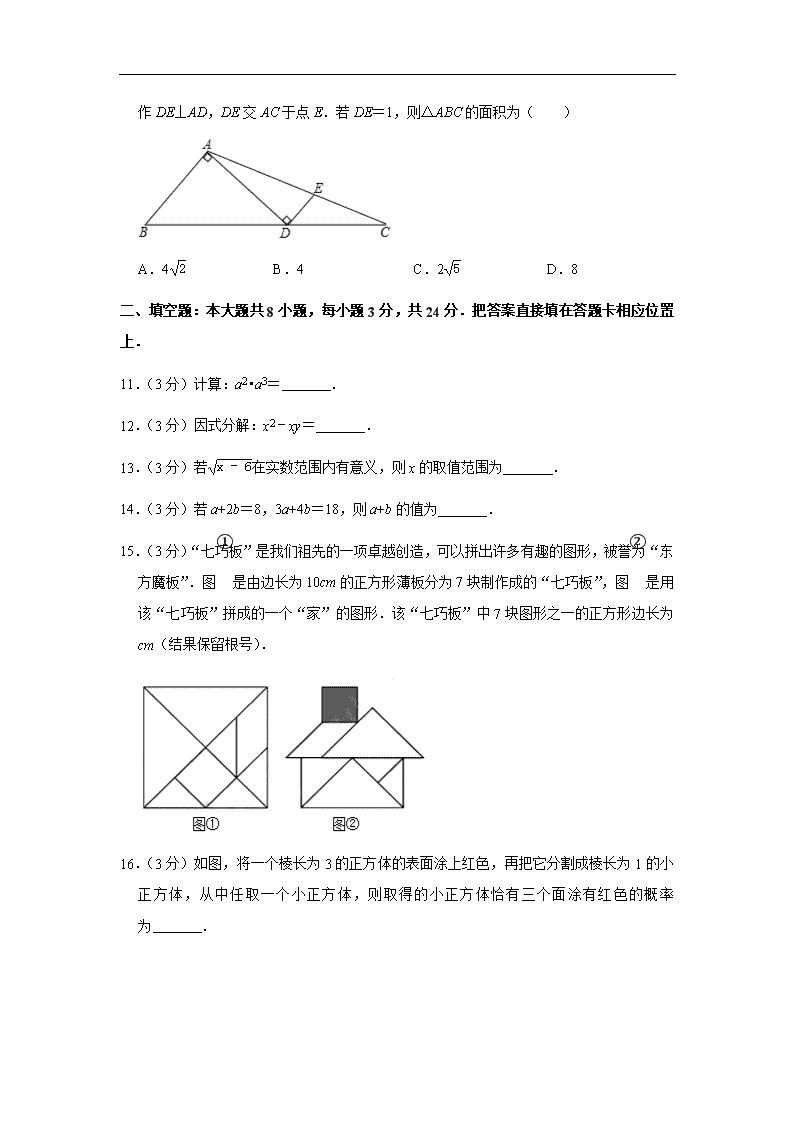10．（3分）如图，在△ABC中，点D为BC边上的一点，且AD＝AB＝2，AD⊥AB．过点D 作DE⊥AD，DE交AC于点E．若DE＝1，则△ABC的面积为（　　）‎ A．4‎2‎ B．4 C．2‎5‎ D．8‎ 二、填空题：本大题共8小题，每小题3分，共24分．把答案直接填在答题卡相应位置上．‎ ‎11．（3分）计算：a2•a3＝　 　．‎ ‎12．（3分）因式分解：x2﹣xy＝　 　．‎ ‎13．（3分）若x-6‎在实数范围内有意义，则x的取值范围为　 　．‎ ‎14．（3分）若a+2b＝8，3a+4b＝18，则a+b的值为　 　．‎ ‎15．（3分）“七巧板”是我们祖先的一项卓越创造，可以拼出许多有趣的图形，被誉为“东方魔板”．图①是由边长为10cm的正方形薄板分为7块制作成的“七巧板”，图②是用该“七巧板”拼成的一个“家”的图形．该“七巧板”中7块图形之一的正方形边长为　 　cm（结果保留根号）．‎ ‎16．（3分）如图，将一个棱长为3的正方体的表面涂上红色，再把它分割成棱长为1的小正方体，从中任取一个小正方体，则取得的小正方体恰有三个面涂有红色的概率为　 　．‎ ‎17．（3分）如图，扇形OAB中，∠AOB＝90°．P为弧AB上的一点，过点P作PC⊥OA，垂足为C，PC与AB交于点D．若PD＝2，CD＝1，则该扇形的半径长为　 　．‎ ‎18．（3分）如图，一块含有45°角的直角三角板，外框的一条直角边长为8cm，三角板的外框线和与其平行的内框线之间的距离均为‎2‎cm，则图中阴影部分的面积为　 　cm2（结果保留根号）．‎ 三、解答题；本大题共10小题，共76分．把解答过程写答题卡相应位置上，解答时应写出必要的计算过程、推演步骤或文字说明，作图时用2B铅笔或黑色墨水签宇笔．‎ ‎19．（5分）计算：（‎3‎）2+|﹣2|﹣（π﹣2）0‎ ‎20．（5分）解不等式组：‎x+1＜5‎‎2(x+4)＞3x+7‎ ‎21．（6分）先化简，再求值：x-3‎x‎2‎‎+6x+9‎‎÷‎（1‎-‎‎6‎x+3‎），其中，x‎=‎2‎-‎3．‎ ‎22．（6分）在一个不透明的盒子中装有4张卡片，4张卡片的正面分别标有数字1，2，3，4，这些卡片除数字外都相同，将卡片搅匀．‎ ‎（1）从盒子中任意抽取一张卡片，恰好抽到标有奇数卡片的概率是　 　；‎ ‎（2）先从盒了中任意抽取一张卡片，再从余下的3张卡片中任意抽取一张卡片，求抽取的2张卡片标有数字之和大于4的概率．（请用画树状图或列表等方法求解）．‎ ‎23．（8分）某校计划组织学生参加“书法”、“摄影”、“航模、“围棋”四个课外兴趣小组，要求每人必须参加，并且只能选择其中一个小组，为了解学生对四个课外兴趣小组的选择情况，学校从全体学生中随机抽取部分学生进行问卷调查，并把调查结果制成如图所示的扇形统计图和条形统计图（部分信息未给出），请你根据给出的信息解答下列问题：‎ ‎（1）求参加这次问卷调查的学生人数，并补全条形统计图（画图后请标注相应的数据）；‎ ‎（2）m＝　 　，n＝　 　；‎ ‎（3）若该校共有1200名学生，试估计该校选择“围棋”课外兴趣小组的学生有多少人？‎ ‎24．（8分）如图，△ABC中，点E在BC边上，AE＝AB，将线段AC绕A点旋转到AF的位置，使得∠CAF＝∠BAE，连接EF，EF与AC交于点G．‎ ‎（1）求证：EF＝BC；‎ ‎（2）若∠ABC＝65°，∠ACB＝28°，求∠FGC的度数．‎ ‎25．（8分）如图，A为反比例函数y‎=‎kx（其中x＞0）图象上的一点，在x轴正半轴上有一点B，OB＝4．连接OA，AB，且OA＝AB＝2‎10‎．‎ ‎（1）求k的值；‎ ‎（2）过点B作BC⊥OB，交反比例函数y‎=‎kx（其中x＞0）的图象于点C，连接OC交AB于点D，求ADDB的值．‎ ‎26．（10分）如图，AB为⊙O的直径，C为⊙O上一点，D是弧BC的中点，BC与AD、OD分别交于点E、F．‎ ‎（1）求证：DO∥AC；‎ ‎（2）求证：DE•DA＝DC2；‎ ‎（3）若tan∠CAD‎=‎‎1‎‎2‎，求sin∠CDA的值．‎ ‎27．（10分）已知矩形ABCD中，AB＝5cm，点P为对角线AC上的一点，且AP＝2‎5‎cm．如图①，动点M从点A出发，在矩形边上沿着A→B→C的方向匀速运动（不包含点C）．设动点M的运动时间为t（s），△APM的面积为S（cm2），S与t的函数关系如图②所示．‎ ‎（1）直接写出动点M的运动速度为　 　cm/s，BC的长度为　 　cm；‎ ‎（2）如图③，动点M重新从点A出发，在矩形边上按原来的速度和方向匀速运动，同时，另一个动点N从点D出发，在矩形边上沿着D→C→B的方向匀速运动，设动点N的运动速度为v（cm/s）．已知两动点M，N经过时间x（s）在线段BC上相遇（不包含点C），动点M，N相遇后立即同时停止运动，记此时△APM与△DPN的面积分别为S1‎ ‎（cm2），S2（cm2）‎ ‎①求动点N运动速度v（cm/s）的取值范围；‎ ‎②试探究S1•S2是否存在最大值，若存在，求出S1•S2的最大值并确定运动时间x的值；若不存在，请说明理由 ‎．‎ ‎28．（10分）如图①，抛物线y＝﹣x2+（a+1）x﹣a与x轴交于A，B两点（点A位于点B的左侧），与y轴交于点C．已知△ABC的面积是6．‎ ‎（1）求a的值；‎ ‎（2）求△ABC外接圆圆心的坐标；‎ ‎（3）如图②，P是抛物线上一点，Q为射线CA上一点，且P、Q两点均在第三象限内，Q、A是位于直线BP同侧的不同两点，若点P到x轴的距离为d，△QPB的面积为2d，且∠PAQ＝∠AQB，求点Q的坐标．‎ ‎2019年江苏省苏州市中考数学试卷 参考答案与试题解析 一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题要求的．请将选择题的答案用2B铅笔涂在答题卡相应位置上．‎ ‎1．（3分）5的相反数是（　　）‎ A．‎1‎‎5‎ B．‎-‎‎1‎‎5‎ C．5 D．﹣5‎ ‎【解答】解：5的相反数是﹣5．‎ 故选：D．‎ ‎2．（3分）有一组数据：2，2，4，5，7，这组数据的中位数为（　　）‎ A．2 B．4 C．5 D．7‎ ‎【解答】解：这组数据排列顺序为：2，2，4，5，7，‎ ‎∴这组数据的中位数为4，‎ 故选：B．‎ ‎3．（3分）苏州是全国重点旅游城市，2018年实现旅游总收入约为26000000万元，数据26000000用科学记数法可表示为（　　）‎ A．0.26×108 B．2.6×108 C．26×106 D．2.6×107‎ ‎【解答】解：将26000000用科学记数法表示为：2.6×107．‎ 故选：D．‎ ‎4．（3分）如图，已知直线a∥b，直线c与直线a，b分别交于点A，B．若∠1＝54°，则∠2等于（　　）‎ A．126° B．134° C．136° D．144°‎ ‎【解答】解：如图所示：‎ ‎∵a∥b，∠1＝54°，‎ ‎∴∠1＝∠3＝54°，‎ ‎∴∠2＝180°﹣54°＝126°．‎ 故选：A．‎ ‎5．（3分）如图，AB为⊙O的切线，切点为A连接AO、BO，BO与⊙O交于点C，延长BO与⊙O交于点D，连接AD．若∠ABO＝36°，则∠ADC的度数为（　　）‎ A．54° B．36° C．32° D．27°‎ ‎【解答】解：∵AB为⊙O的切线，‎ ‎∴∠OAB＝90°，‎ ‎∵∠ABO＝36°，‎ ‎∴∠AOB＝90°﹣∠ABO＝54°，‎ ‎∵OA＝OD，‎ ‎∴∠ADC＝∠OAD，‎ ‎∵∠AOB＝∠ADC+∠OAD，‎ ‎∴∠ADC‎=‎‎1‎‎2‎∠AOB＝27°；‎ 故选：D．‎ ‎6．（3分）小明用15元买售价相同的软面笔记本，小丽用24元买售价相同的硬面笔记本（两人的钱恰好用完），已知每本硬面笔记本比软面笔记本贵3元，且小明和小丽买到相同数量的笔记本，设软面笔记本每本售价为x元，根据题意可列出的方程为（　　）‎ A．‎15‎x‎=‎‎24‎x+3‎ B．‎15‎x‎=‎‎24‎x-3‎ C．‎15‎x+3‎‎=‎‎24‎x D．‎‎15‎x-3‎‎=‎‎24‎x ‎【解答】解：设软面笔记本每本售价为x元，‎ 根据题意可列出的方程为：‎15‎x‎=‎‎24‎x+3‎．‎ 故选：A．‎ ‎7．（3分）若一次函数y＝kx+b（k，b为常数，且k≠0）的图象经过点A（0，﹣1），B（1，1），则不等式kx+b＞1的解为（　　）‎ A．x＜0 B．x＞0 C．x＜1 D．x＞1‎ ‎【解答】解：如图所示：不等式kx+b＞1的解为：x＞1．‎ 故选：D．‎ ‎8．（3分）如图，小亮为了测量校园里教学楼AB的高度，将测角仪CD竖直放置在与教学楼水平距离为18‎3‎m的地面上，若测角仪的高度是1.5m．测得教学楼的顶部A处的仰角为30°．则教学楼的高度是（　　）‎ A．55.5m B．54m C．19.5m D．18m ‎【解答】解：过D作DE⊥AB，‎ ‎∵在D处测得旗杆顶端A的仰角为30°，‎ ‎∴∠ADE＝30°，‎ ‎∵BC＝DE＝18‎3‎m，‎ ‎∴AE＝DE•tan30°＝18m，‎ ‎∴AB＝AE+BE＝AE+CD＝18+1.5＝19.5m，‎ 故选：C．‎ ‎9．（3分）如图，菱形ABCD的对角线AC，BD交于点O，AC＝4，BD＝16，将△ABO沿点A到点C的方向平移，得到△A'B'O'．当点A'与点C重合时，点A与点B'之间的距离为（　　）‎ A．6 B．8 C．10 D．12‎ ‎【解答】解：∵四边形ABCD是菱形，‎ ‎∴AC⊥BD，AO＝OC‎=‎‎1‎‎2‎AC＝2，OB＝OD‎=‎‎1‎‎2‎BD＝8，‎ ‎∵△ABO沿点A到点C的方向平移，得到△A'B'O'，点A'与点C重合，‎ ‎∴O'C＝OA＝2，O'B'＝OB＝8，∠CO'B'＝90°，‎ ‎∴AO'＝AC+O'C＝6，‎ ‎∴AB'‎=O'B'‎‎2‎‎+‎AO'‎‎2‎=‎8‎‎2‎‎+‎‎6‎‎2‎=‎10；‎ 故选：C．‎ ‎10．（3分）如图，在△ABC中，点D为BC边上的一点，且AD＝AB＝2，AD⊥AB．过点D作DE⊥AD，DE交AC于点E．若DE＝1，则△ABC的面积为（　　）‎ A．4‎2‎ B．4 C．2‎5‎ D．8‎ ‎【解答】解：∵AB⊥AD，AD⊥DE，‎ ‎∴∠BAD＝∠ADE＝90°，‎ ‎∴DE∥AB，‎ ‎∴∠CED＝∠CAB，‎ ‎∵∠C＝∠C，‎ ‎∴△CED∽△CAB，‎ ‎∵DE＝1，AB＝2，即DE：AB＝1：2，‎ ‎∴S△DEC：S△ACB＝1：4，‎ ‎∴S四边形ABDE：S△ACB＝3：4，‎ ‎∵S四边形ABDE＝S△ABD+S△ADE‎=‎1‎‎2‎×‎2×2‎+‎1‎‎2‎×‎2×1＝2+1＝3，‎ ‎∴S△ACB＝4，‎ 故选：B．‎ 二、填空题：本大题共8小题，每小题3分，共24分．把答案直接填在答题卡相应位置上．‎ ‎11．（3分）计算：a2•a3＝　a5　．‎ ‎【解答】解：a2•a3＝a2+3＝a5．‎ 故答案为：a5．‎ ‎12．（3分）因式分解：x2﹣xy＝　x（x﹣y）　．‎ ‎【解答】解：x2﹣xy＝x（x﹣y）．‎ 故答案为：x（x﹣y）．‎ ‎13．（3分）若x-6‎在实数范围内有意义，则x的取值范围为　x≥6　．‎ ‎【解答】解：若x-6‎在实数范围内有意义，‎ 则x﹣6≥0，‎ 解得：x≥6．‎ 故答案为：x≥6．‎ ‎14．（3分）若a+2b＝8，3a+4b＝18，则a+b的值为　5　．‎ ‎【解答】解：∵a+2b＝8，3a+4b＝18，‎ 则a＝8﹣2b，‎ 代入3a+4b＝18，‎ 解得：b＝3，‎ 则a＝2，‎ 故a+b＝5．‎ 故答案为：5．‎ ‎15．（3分）“七巧板”是我们祖先的一项卓越创造，可以拼出许多有趣的图形，被誉为“东方魔板”．图①是由边长为10cm的正方形薄板分为7块制作成的“七巧板”，图②是用该“七巧板”拼成的一个“家”的图形．该“七巧板”中7块图形之一的正方形边长为　‎5‎‎2‎‎2‎　cm（结果保留根号）．‎ ‎【解答】解：10×10＝100（cm2）‎ ‎100‎‎8‎‎=‎‎5‎‎2‎‎2‎‎（cm）‎ 答：该“七巧板”中7块图形之一的正方形边长为‎5‎‎2‎‎2‎cm．‎ 故答案为：‎5‎‎2‎‎2‎．‎ ‎16．（3分）如图，将一个棱长为3的正方体的表面涂上红色，再把它分割成棱长为1的小正方体，从中任取一个小正方体，则取得的小正方体恰有三个面涂有红色的概率为　‎8‎‎27‎　．‎ ‎【解答】解：由题意可得：小立方体一共有27个，恰有三个面涂有红色的有8个，‎ 故取得的小正方体恰有三个面涂有红色的概率为：‎8‎‎27‎．‎ 故答案为：‎8‎‎27‎．‎ ‎17．（3分）如图，扇形OAB中，∠AOB＝90°．P为弧AB上的一点，过点P作PC⊥OA，垂足为C，PC与AB交于点D．若PD＝2，CD＝1，则该扇形的半径长为　5　．‎ ‎【解答】解：连接OP，如图所示．‎ ‎∵OA＝OB，∠AOB＝90°，‎ ‎∴∠OAB＝45°．‎ ‎∵PC⊥OA，‎ ‎∴△ACD为等腰直角三角形，‎ ‎∴AC＝CD＝1．‎ 设该扇形的半径长为r，则OC＝r﹣1，‎ 在Rt△POC中，∠PCO＝90°，PC＝PD+CD＝3，‎ ‎∴OP2＝OC2+PC2，即r2＝（r﹣1）2+9，‎ 解得：r＝5．‎ 故答案为：5．‎ ‎18．（3分）如图，一块含有45°角的直角三角板，外框的一条直角边长为8cm，三角板的外框线和与其平行的内框线之间的距离均为‎2‎cm，则图中阴影部分的面积为　（10‎+12‎‎2‎）　cm2（结果保留根号）．‎ ‎【解答】解：如图，‎ EF＝DG＝CH‎=‎‎2‎，‎ ‎∵含有45°角的直角三角板，‎ ‎∴BC‎=‎‎2‎，GH＝2，‎ ‎∴FG＝8‎-‎2‎-‎2‎-‎2‎=‎6﹣2‎2‎，‎ ‎∴图中阴影部分的面积为：‎ ‎8×8÷2﹣（6﹣2‎2‎）×（6﹣2‎2‎）÷2‎ ‎＝32﹣22+12‎‎2‎ ‎＝10+12‎2‎（cm2）‎ 答：图中阴影部分的面积为（10‎+12‎‎2‎）cm2．‎ 故答案为：（10‎+12‎‎2‎）．‎ 三、解答题；本大题共10小题，共76分．把解答过程写答题卡相应位置上，解答时应写出必要的计算过程、推演步骤或文字说明，作图时用2B铅笔或黑色墨水签宇笔．‎ ‎19．（5分）计算：（‎3‎）2+|﹣2|﹣（π﹣2）0‎ ‎【解答】解：原式＝3+2﹣1‎ ‎＝4．‎ ‎20．（5分）解不等式组：‎x+1＜5‎‎2(x+4)＞3x+7‎ ‎【解答】解：解不等式x+1＜5，得：x＜4，‎ 解不等式2（x+4）＞3x+7，得：x＜1，‎ 则不等式组的解集为x＜1．‎ ‎21．（6分）先化简，再求值：x-3‎x‎2‎‎+6x+9‎‎÷‎（1‎-‎‎6‎x+3‎），其中，x‎=‎2‎-‎3．‎ ‎【解答】解：原式‎=x-3‎‎(x+3‎‎)‎‎2‎÷‎（x+3‎x+3‎‎-‎‎6‎x+3‎）‎ ‎=x-3‎‎(x+3‎‎)‎‎2‎÷‎x-3‎x+3‎‎ ‎ ‎=‎x-3‎‎(x+3‎‎)‎‎2‎‎•x+3‎x-3‎ ‎ ‎=‎‎1‎x+3‎‎，‎ 当x‎=‎2‎-‎3时，‎ 原式‎=‎1‎‎2‎‎-3+3‎=‎1‎‎2‎=‎‎2‎‎2‎．‎ ‎22．（6分）在一个不透明的盒子中装有4张卡片，4张卡片的正面分别标有数字1，2，3，4，这些卡片除数字外都相同，将卡片搅匀．‎ ‎（1）从盒子中任意抽取一张卡片，恰好抽到标有奇数卡片的概率是　‎1‎‎2‎　；‎ ‎（2）先从盒了中任意抽取一张卡片，再从余下的3张卡片中任意抽取一张卡片，求抽取的2张卡片标有数字之和大于4的概率．（请用画树状图或列表等方法求解）．‎ ‎【解答】解：（1）从盒子中任意抽取一张卡片，恰好抽到标有奇数卡片的概率是为‎2‎‎4‎‎=‎‎1‎‎2‎，‎ 故答案为：‎1‎‎2‎．‎ ‎（2）根据题意列表得：‎ ‎ ‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎1‎ ‎3‎ ‎4‎ ‎5‎ ‎2‎ ‎3‎ ‎5‎ ‎6‎ ‎3‎ ‎4‎ ‎5‎ ‎7‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ 由表可知，共有12种等可能结果，其中抽取的2张卡片标有数字之和大于4的有8种结果，‎ 所以抽取的2张卡片标有数字之和大于4的概率为‎8‎‎12‎‎=‎‎2‎‎3‎．‎ ‎23．（8分）某校计划组织学生参加“书法”、“摄影”、“航模、“围棋”四个课外兴趣小组，要求每人必须参加，并且只能选择其中一个小组，为了解学生对四个课外兴趣小组的选择情况，学校从全体学生中随机抽取部分学生进行问卷调查，并把调查结果制成如图所示的扇形统计图和条形统计图（部分信息未给出），请你根据给出的信息解答下列问题：‎ ‎（1）求参加这次问卷调查的学生人数，并补全条形统计图（画图后请标注相应的数据）；‎ ‎（2）m＝　36　，n＝　16　；‎ ‎（3）若该校共有1200名学生，试估计该校选择“围棋”课外兴趣小组的学生有多少人？‎ ‎【解答】解：（1）参加这次问卷调查的学生人数为30÷20%＝150（人），‎ 航模的人数为150﹣（30+54+24）＝42（人），‎ 补全图形如下：‎ ‎（2）m%‎=‎54‎‎150‎×‎100%＝36%，n%‎=‎24‎‎150‎×‎100%＝16%，‎ 即m＝36、n＝16，‎ 故答案为：36、16；‎ ‎（3）估计该校选择“围棋”课外兴趣小组的学生有1200×16%＝192（人）．‎ ‎24．（8分）如图，△ABC中，点E在BC边上，AE＝AB，将线段AC绕A点旋转到AF的位置，使得∠CAF＝∠BAE，连接EF，EF与AC交于点G．‎ ‎（1）求证：EF＝BC；‎ ‎（2）若∠ABC＝65°，∠ACB＝28°，求∠FGC的度数．‎ ‎【解答】（1）证明：∵∠CAF＝∠BAE，‎ ‎∴∠BAC＝∠EAF．‎ ‎∵将线段AC绕A点旋转到AF的位置，‎ ‎∴AC＝AF．‎ 在△ABC与△AEF中，‎ AB=AE‎∠BAC=∠EAFAC=AF‎，‎ ‎∴△ABC≌△AEF（SAS），‎ ‎∴EF＝BC；‎ ‎（2）解：∵AB＝AE，∠ABC＝65°，‎ ‎∴∠BAE＝180°﹣65°×2＝50°，‎ ‎∴∠FAG＝∠BAE＝50°．‎ ‎∵△ABC≌△AEF，‎ ‎∴∠F＝∠C＝28°，‎ ‎∴∠FGC＝∠FAG+∠F＝50°+28°＝78°．‎ ‎25．（8分）如图，A为反比例函数y‎=‎kx（其中x＞0）图象上的一点，在x轴正半轴上有一点B，OB＝4．连接OA，AB，且OA＝AB＝2‎10‎．‎ ‎（1）求k的值；‎ ‎（2）过点B作BC⊥OB，交反比例函数y‎=‎kx（其中x＞0）的图象于点C，连接OC交AB于点D，求ADDB的值．‎ ‎【解答】解：（1）过点A作AH⊥x轴，垂足为点H，AH交OC于点M，如图所示．‎ ‎∵OA＝AB，AH⊥OB，‎ ‎∴OH＝BH‎=‎‎1‎‎2‎OB＝2，‎ ‎∴AH‎=OA‎2‎-OH‎2‎=‎6，‎ ‎∴点A的坐标为（2，6）．‎ ‎∵A为反比例函数y‎=‎kx图象上的一点，‎ ‎∴k＝2×6＝12．‎ ‎（2）∵BC⊥x轴，OB＝4，点C在反比例函数y‎=‎‎12‎x上，‎ ‎∴BC‎=kOB=‎3．‎ ‎∵AH∥BC，OH＝BH，‎ ‎∴MH‎=‎‎1‎‎2‎BC‎=‎‎3‎‎2‎，‎ ‎∴AM＝AH﹣MH‎=‎‎9‎‎2‎．‎ ‎∵AM∥BC，‎ ‎∴△ADM∽△BDC，‎ ‎∴ADDB‎=AMBC=‎‎3‎‎2‎．‎ ‎26．（10分）如图，AB为⊙O的直径，C为⊙O上一点，D是弧BC的中点，BC与AD、OD分别交于点E、F．‎ ‎（1）求证：DO∥AC；‎ ‎（2）求证：DE•DA＝DC2；‎ ‎（3）若tan∠CAD‎=‎‎1‎‎2‎，求sin∠CDA的值．‎ ‎【解答】解：（1）∵点D是BC中点，OD是圆的半径，‎ ‎∴OD⊥BC，‎ ‎∵AB是圆的直径，‎ ‎∴∠ACB＝90°，‎ ‎∴AC∥OD；‎ ‎（2）∵CD‎=‎BD，‎ ‎∴∠CAD＝∠DCB，‎ ‎∴△DCE∽△DCA，‎ ‎∴CD2＝DE•DA；‎ ‎（3）∵tan∠CAD‎=‎‎1‎‎2‎，‎ ‎∴△DCE和△DAC的相似比为：‎1‎‎2‎，‎ 设：DE＝a，则CD＝2a，AD＝4a，AE＝3a，‎ ‎∴AEDE‎=‎3，‎ 即△AEC和△DEF的相似比为3，‎ 设：EF＝k，则CE＝3k，BC＝8k，‎ tan∠CAD‎=‎‎1‎‎2‎，‎ ‎∴AC＝6k，AB＝10k，‎ ‎∴sin∠CDA‎=‎‎3‎‎5‎．‎ ‎27．（10分）已知矩形ABCD中，AB＝5cm，点P为对角线AC上的一点，且AP＝2‎5‎cm．如图①，动点M从点A出发，在矩形边上沿着A→B→C的方向匀速运动（不包含点C）．设动点M的运动时间为t（s），△APM的面积为S（cm2），S与t的函数关系如图②所示．‎ ‎（1）直接写出动点M的运动速度为　2　cm/s，BC的长度为　10　cm；‎ ‎（2）如图③，动点M重新从点A出发，在矩形边上按原来的速度和方向匀速运动，同时，另一个动点N从点D出发，在矩形边上沿着D→C→B的方向匀速运动，设动点N的运动速度为v（cm/s）．已知两动点M，N经过时间x（s）在线段BC上相遇（不包含点C），动点M，N相遇后立即同时停止运动，记此时△APM与△DPN的面积分别为S1（cm2），S2（cm2）‎ ‎①求动点N运动速度v（cm/s）的取值范围；‎ ‎②试探究S1•S2是否存在最大值，若存在，求出S1•S2的最大值并确定运动时间x的值；若不存在，请说明理由 ‎．‎ ‎【解答】解：（1）∵t＝2.5s时，函数图象发生改变，‎ ‎∴t＝2.5s时，M运动到点B处，‎ ‎∴动点M的运动速度为：‎5‎‎2.5‎‎=‎2cm/s，‎ ‎∵t＝7.5s时，S＝0，‎ ‎∴t＝7.5s时，M运动到点C处，‎ ‎∴BC＝（7.5﹣2.5）×2＝10（cm），‎ 故答案为：2，10；‎ ‎（2）①∵两动点M，N在线段BC上相遇（不包含点C），‎ ‎∴当在点C相遇时，v‎=‎5‎‎7.5‎=‎‎2‎‎3‎（cm/s），‎ 当在点B相遇时，v‎=‎5+10‎‎2.5‎=‎6（cm/s），‎ ‎∴动点N运动速度v（cm/s）的取值范围为‎2‎‎3‎cm/s＜v≤6cm/s；‎ ‎②过P作EF⊥AB于F，交CD于E，如图3所示：‎ 则EF∥BC，EF＝BC＝10，‎ ‎∴AFAB‎=‎APAC，‎ ‎∵AC‎=AB‎2‎+BC‎2‎=‎5‎5‎，‎ ‎∴AF‎5‎‎=‎‎2‎‎5‎‎5‎‎5‎，‎ 解得：AF＝2，‎ ‎∴DE＝AF＝2，CE＝BF＝3，PF‎=AP‎2‎-AF‎2‎=‎4，‎ ‎∴EP＝EF﹣PF＝6，‎ ‎∴S1＝S△APM＝S△APF+S梯形PFBM﹣S△ABM‎=‎1‎‎2‎×‎4×2‎+‎‎1‎‎2‎（4+2x﹣5）×3‎-‎1‎‎2‎×‎5×（2x﹣5）＝﹣2x+15，‎ S2＝S△DPM＝S△DEP+S梯形EPMC﹣S△DCM‎=‎1‎‎2‎×‎2×6‎+‎‎1‎‎2‎（6+15﹣2x）×3‎-‎1‎‎2‎×‎5×（15﹣2x）＝2x，‎ ‎∴S1•S2＝（﹣2x+15）×2x＝﹣4x2+30x＝﹣4（x‎-‎‎15‎‎4‎）2‎+‎‎225‎‎4‎，‎ ‎∵2.5‎＜‎15‎‎4‎＜‎7.5，在BC边上可取，‎ ‎∴当x‎=‎‎15‎‎4‎时，S1•S2的最大值为‎225‎‎4‎．‎ ‎28．（10分）如图①，抛物线y＝﹣x2+（a+1）x﹣a与x轴交于A，B两点（点A位于点B的左侧），与y轴交于点C．已知△ABC的面积是6．‎ ‎（1）求a的值；‎ ‎（2）求△ABC外接圆圆心的坐标；‎ ‎（3）如图②，P是抛物线上一点，Q为射线CA上一点，且P、Q两点均在第三象限内，Q、A是位于直线BP同侧的不同两点，若点P到x轴的距离为d，△QPB的面积为2d，且∠PAQ＝∠AQB，求点Q的坐标．‎ ‎【解答】解：（1）‎ ‎∵y＝﹣x2+（a+1）x﹣a 令y＝0，即﹣x2+（a+1）x﹣a＝0‎ 解得x1＝a，x2＝1‎ 由图象知：a＜0‎ ‎∴A（a，0），B（1，0）‎ ‎∵s△ABC＝6‎ ‎∴‎‎1‎‎2‎‎(1-a)(-a)=6‎ 解得：a＝﹣3，（a＝4舍去）‎ ‎（2）设直线AC：y＝kx+b，‎ 由A（﹣3，0），C（0，3），‎ 可得﹣3k+b＝0，且b＝3‎ ‎∴k＝1‎ 即直线AC：y＝x+3，‎ A、C的中点D坐标为（‎-‎‎3‎‎2‎，‎3‎‎2‎）‎ ‎∴线段AC的垂直平分线解析式为：y＝﹣x，‎ 线段AB的垂直平分线为x＝﹣1‎ 代入y＝﹣x，‎ 解得：y＝1‎ ‎∴△ABC外接圆圆心的坐标（﹣1，1）‎ ‎（3）‎ 作PM⊥x轴，则 s‎△BAP‎=‎1‎‎2‎AB⋅PM=‎1‎‎2‎×4×d‎ ‎ ‎∵‎s‎△PQB‎=‎S‎△PAB ‎∴A、Q到PB的距离相等，∴AQ∥PB 设直线PB解析式为：y＝x+b ‎∵直线经过点B（1，0）‎ 所以：直线PB的解析式为y＝x﹣1‎ 联立y=‎-x‎2‎-2x+3‎y=x-1‎ 解得：‎x=-4‎y=-5‎ ‎∴点P坐标为（﹣4，﹣5）‎ 又∵∠PAQ＝∠AQB 可得：△PBQ≌△ABP（AAS）‎ ‎∴PQ＝AB＝4‎ 设Q（m，m+3）‎ 由PQ＝4得：‎ ‎(m+4‎)‎‎2‎+(m+3+5‎)‎‎2‎=‎‎4‎‎2‎‎ ‎ 解得：m＝﹣4，m＝﹣8（舍去）‎ ‎∴Q坐标为（﹣4，﹣1）‎ 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/6/30 10:01:06；用户：中考培优辅导；邮箱：p5193@xyh.com；学号：27411521‎